Список непериодичных наборов плиток

В геометрии замощение — это разбиение плоскости (или другой геометрической структуры) на замкнутые множества (называемые плитками) без промежутков и наложений (отличных от границ плиток)^[1]. Замощение считается периодическим, если существуют параллельные переносы в двух независимых направлениях, которые переносят плитки в точно такие же. Такое замощение состоит из одной фундаментальной единицы или примитивной ячейки, которые повторяются бесконечно в двух независимых направлениях^[2]. Пример такого замощения показан на иллюстрации справа. Замощения, которые нельзя построить из единственной примитивной ячейки, называются непериодичными. Если данный набор плиток позволяет только непериодичное замощение, такой набор называется непериодичным^[3].

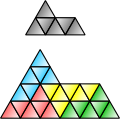
Нажмите «показать» для описания.

Периодическая мозаика^[англ.] с выделенной фундаментальной единицей (треугольник) и примитивной ячейкой (шестиугольник). Замощение всей плоскости может быть получено путём сборки копий треугольных «заплат» вместе. Чтобы это сделать, базовый треугольник следует повернуть, чтобы присоединить к соседнему треугольнику. Другая фигура, нарисованная на замощении, белый шестиугольник, представляет примитивную ячейку мозаики. Копии соответствующей фигуры (с рисунком) могут быть параллельно перенесены для образования бесконечной мозаики на плоскости, при этом нет необходимости вращать выделенный участок, чтобы получить замощение.

Первая таблица объясняет сокращения, используемые во второй таблице. Вторая таблица содержит все известные непериодичные наборы плиток и даёт некоторую дополнительную базовую информацию о каждом наборе. Этот список плиток остаётся неполным.

Объяснения

Сокращение	Значение	Объяснение
E2	Евклидова плоскость	обычная плоскость
H2	Гиперболическая плоскость	плоскость, где не выполняется аксиома параллельности
E3	Евклидово трёхмерное пространство	пространство, определённое тремя перпендикулярными осями координат
ЛВП	Локально взаимно производные	говорят, что две плитки локально взаимно производные друг из друга, если одна плитка получается из другой простым локальным правилом (таким как удаление или вставка ребра)

Список

Рисунок	Название	Число плиток	Простран- ство	Дата публикации	Ссылки	Комментарии
	Плитки «Трилобит» и «Крест»	2	E2	1999	[4]	ЛВП с плитками «Стул» (квадрат с вырезанной четвертинкой)
	Плитки Пенроуза P1	6	E2	1974[Note 1]	[5]	ЛВП с плитками P2 и P3, треугольниками Робинсона и плитками «звезда, лодка, шестиугольник»
	Плитки Пенроуза P2	2	E2	1977[Note 2]	[6]	ЛВП с плитками P1 и P3, треугольниками Робинсона и плитками «звезда, лодка, шестиугольник»
	Плитки Пенроуза P3	2	E2	1978[Note 3]	[7]	ЛВП с плитками P1 и P2, треугольниками Робинсона и плитками «звезда, лодка, шестиугольник»
	Двойные плитки	2	E2	1988	[8] [9]	Хотя плитки похожи на плитки из P3, плитки не являются ЛВП друг из друга. Мозаика разработана в попытках смоделировать расположение атомов в двойных сплавах
	Плитки Робинсона[англ.]	6	E2	1971[Note 4]	[10]	Плитки обеспечивают непериодичность путём образования бесконечной иерархии квадратных решёток
Нет рисунка	Плитки Амманна A1	6	E2	1977[11]	[12]	Плитки обеспечивают непериодичность путём образования бесконечного иерархического двоичного дерева.
	Плитки Амманна A2	2	E2	1986[Note 5]	[13]
	Плитки Амманна A3	3	E2	1986[Note 5]	[13]
	Плитки Амманна A4	2	E2	1986[Note 5]	[13][14]	ЛВП с плитками Амманна A5.
	Плитки Амманна A5	2	E2	1982[Note 6]	[15] [16]	ЛВП с плитками Амманна A4.
Нет рисунка	Плитки Пенроуза «Шестиугольник, Треугольник»	2	E2	1997[17]	[17][18]
Нет рисунка	Плитки «Золотой треугольник»[19]	10	E2	2001[20]	[21]	Дата соответствует времени открытия правил соединения. Двойственные плиткам Амманна A2
	Плитки Соколара	3	E2	1989[Note 7]	[22][23]	ЛВП с плитками «Щит»
	Плитки «Щит»	4	E2	1988[Note 8]	[24][25]	ЛВП с плитками Соколара
	Плитки «Квадрат, Треугольник»	5	E2	1986[26]	[27]
	Мозаика «Сфинкс»	91	E2		[28]
	Плитки «Звезда, лодка, шестиугольник»	3	E2		[29][30][31]	ЛВП с плитками Пенроуза P1, P2, P3 и треугольниками Робинсона
	Треугольник Робинсона	4	E2		[12]	Плитки ЛВП с плитками Пенроуза P1, P2, P3 и «Звезда, лодка, шестиугольник».
	Треугольники Данцера	6	E2	1996[32]	[33]
	Плитки «Вертушка»		E2	1994[34][35]	[36][37]	Дата соответствует публикации правил соединения.
	Плитка Соколара — Тейлор	1	E2	2010	[38][39]	Несвязная плитка. Непериодичная иерархическая мозаика.
Нет рисунка	Плитки Вана	20426	E2	1966	[40]
Нет рисунка	Плитки Вана	104	E2	2008	[41]
Нет рисунка	Плитки Вана	52	E2	1971[Note 4]	[42]	Плитки обеспечивают непериодичность путём образования бесконечной иерархии квадратных решёток
	Плитки Вана	32	E2	1986	[43]	локально производные из плиток Пенроуза.
Нет рисунка	Плитки Вана	24	E2	1986	[43]	локально производные из плиток A2
	Плитки Вана	16	E2	1986	[44] [45]	Производные из плиток A2 и их полос Амманна
	Плитки Вана	14	E2	1996	[46][47]
	Плитки Вана	13	E2	1996	[48][49]
Нет рисунка	Плитка «Десятиугольная губка»	1	E2	2002	[50][51]	Пористая плитка, состоящая из непересекающихся множеств точек
Нет рисунка	Строго непериодичные плитки Гудмана-Страусса	85	H2	2005	[52]
Нет рисунка	Строго непериодичные плитки Гудмана-Страусса	26	H2	2005	[53]
	Гиперболическая плитка Бороцки (Böröczky)	1	Hn	1974[54]	[55][56]	Лишь слабо непериодична
Нет рисунка	Плитка Шмитта	1	E3	1988	[57]	периодична по винту[англ.]
	Плитка Шмитта—Конвея—Данцера	1	E3		[57]	периодична по винту[англ.] и выпукла
	Плитка Соколара — Тейлор	1	E3	2010	[38][39]	Периодична в третьем измерении
Нет рисунка	Ромбоэдр Пенроуза	2	E3	1981[58]	[59][60][61][62][63][64][65]
	Ромбоэдры Макея-Амманна	4	E3	1981	[66]	Обладают икосаэдральной симметрией. Это декорированные ромбоэдры Пенроуза с правилами соединения, обеспечивающими непериодичность.
Нет рисунка	Кубики Вана	21	E3	1996	[67]
Нет рисунка	Кубики Вана	18	E3	1999	[68]
Нет рисунка	Тетраэдры Данцера	4	E3	1989[69]	[70]
	Плитки I и L	2	En для всех n ≥ 3	1999	[71]
	«Шляпа»	1	E2	2023		замощение использует плитку вместе с её зеркальным отражением
	«Привидение»	1	E2	2023		полное решение задачи одной плитки в плоскости