Disperzija (optika)

Disperzíja ali razklòn je v optiki pojav, ki se kaže v tem, da je fazna hitrost valovanja (v splošnem elektromagnetnega valovanja in tudi poljubnega valovanja) odvisna od frekvence.^[1] Včasih se ta vrsta odvisnosti imenuje tudi kromatična disperzija. Nastane zaradi tega, ker je lomni količnik odvisen od valovne dolžine svetlobe (frekvence). Opazi se lahko tudi disperzijo skupinske hitrosti.

Po prehodu bele svetlobe skozi optično prizmo se zaradi odvisnosti lomnega količnika od valovne dolžine na drugi strani pojavi cel spekter barv (mavrico).

Za druge pomene glej disperzija (razločitev).

Pojav je odkril Isaac Newton (1642–1727) okoli leta 1672, pojasnili pa so ga mnogo let pozneje.

Najenostavnješi zgled za prikaz disperzije je prehod bele svetlobe preko optične prizme (glej sliko na desni strani). Najbolj znan pojav, ki nastane zaradi disperzije svetlobe, je mavrica. Posledica disperzije je tudi kromatična aberacija, ki je ena izmed napak optičnih naprav.

Disperzija fazne hitrosti

Fazna hitrost je določena kot ${\displaystyle v_{\rm {p}}={\frac {\omega }{k}}}$. Pokazatelj odvisnosti lomnega količnika od valovne dolžine je ${\displaystyle {\frac {\mathrm {d} n(\lambda )}{\mathrm {d} \lambda }}\!}$ ali disperzija fazne hitrosti. Kadar je ta vrednost negativna, je disperzija normalna. Kadar pa je pozitivna, se govori o nenormalni disperziji. Pri normalni disperziji je torej:

${\displaystyle {\frac {\mathrm {d} n}{\mathrm {d} \lambda }}<0\!\,,}$

To pomeni, da vrednost lomnega količnika pada kadar valovna dolžina svetlobe raste. To pomeni, da je lomni količnik rdeče svetlobe manjši od lomnega količnika rumene svetlobe, ta pa je manjši od lomnega količnika modre svetlobe. Fazna hitrost svetlobe v poljubnem sredstvu je podana z:

${\displaystyle v={\frac {c}{n}}\!\,,}$

kjer je:

• ${\displaystyle v\!}$ fazna hitrost svetlobe
• ${\displaystyle c\!}$ hitrost svetlobe
• ${\displaystyle n\!}$ lomni količnik sredstva

V splošnem je lomni količnik funkcija frekvence ${\displaystyle n=n(\nu )\!}$ oziroma valovne dolžine ${\displaystyle n=n(\lambda )\!}$. Oblika funkcije je odvisna od snovi. Opiše se s Cauchyjevo in tudi s Sellmeierjevo enačbo.

Skupinska hitrost pove kako hitro se gibljejo spremembe v amplitudi valovanja.

Disperzija skupinske hitrosti

Če se skupinsko hitrost označi z ${\displaystyle v_{\rm {g}}\!}$, potem velja naslednja zveza med fazno in skupinsko hitrostjo:

${\displaystyle v_{\rm {g}}=v_{\rm {p}}-\lambda {\frac {\mathrm {d} v_{\rm {p}}}{\mathrm {d} \lambda }}\!\,,}$

kjer je:

• ${\displaystyle v_{\rm {p}}\!}$ fazna hitrost svetlobe
• ${\displaystyle \lambda \!}$ valovna dolžina svetlobe v vakuumu

Skupinska hitrost je določena kot ${\displaystyle v_{\rm {g}}={\frac {\partial \omega }{\partial k}}}$.

Skupinska hitrost običajno tudi določa, kako hitro se giblje energija vzdolž smeri gibanja valovanja. Lahko se tudi reče, da pove, kako hitro se giblje sprememba amplitude (znana tudi kot ovojnica valovanja)

Splošna formulacija visokih redov disperzije – Lah-Laguerrova optika

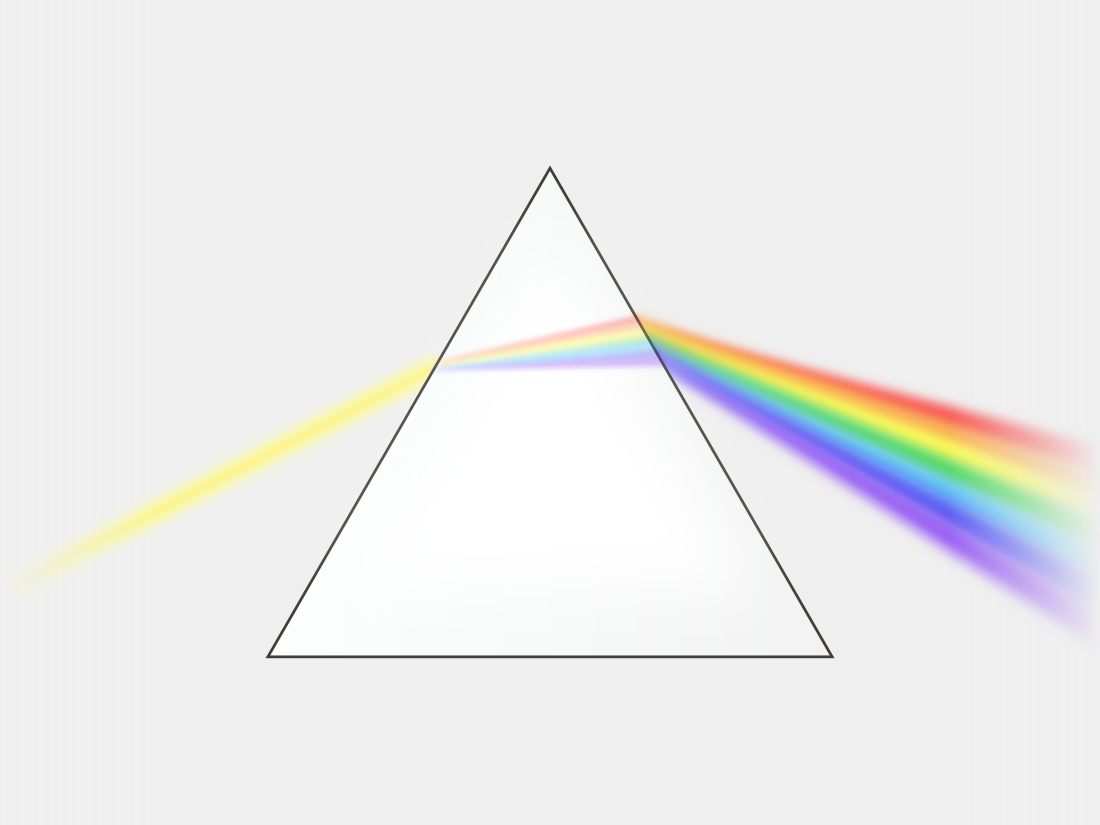
Opis kromatične disperzije na perturbativen način s Taylorjevimi koeficienti je koristen za optimizacijske probleme, pri katerih je treba uravnotežiti disperzijo iz več različnih sistemov. Na primer, v laserskih ojačevalnikih s kirpskimi impulzi se impulzi najprej časovno raztegnejo z raztegovalnikom, da se preprečijo optične poškodbe. Nato se v procesu ojačitve impulzi neizogibno kopičijo v linearni in nelinearni fazi, ki prehaja skozi materiale. In nazadnje se impulzi stisnejo v različnih vrstah kompresorjev. Za izničenje morebitnih preostalih višjih redov v nakopičeni fazi se običajno posamezni redi izmerijo in uravnotežijo. Vendar pri enotnih sistemih takšen perturbacijski opis pogosto ni potreben (npr. širjenje v valovodih). Disperzijski redi so bili posplošeni na računsko prijazen način v obliki transformacij tipa Lah-Laguerre.^[2][3]

Disperzijski redi so določeni s Taylorjevim razvojem faze ali valovnega vektorja.

${\displaystyle {\begin{array}{c}\varphi \mathrm {(} \omega \mathrm {)} =\varphi \left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial \varphi }{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}\varphi }{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}\varphi }{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}$

${\displaystyle {\begin{array}{c}k\mathrm {(} \omega \mathrm {)} =k\left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial k}{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}k}{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}k}{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}$

Disperzijska razmerja za valovanje ${\displaystyle k\mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}n\mathrm {(} \omega \mathrm {)} }$ in fazo ${\displaystyle \varphi \mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}{\it {OP}}\mathrm {(} \omega \mathrm {)} }$ lahko izrazimo kot:

${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}k\mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}n\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}n\mathrm {(} \omega \mathrm {)} \right)\ \end{array}}}$, ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}\varphi \mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} \right)\end{array}}(1)}$

Odvodi vsake diferencirane funkcije ${\displaystyle f\mathrm {(} \omega \mathrm {|} \lambda \mathrm {)} }$ v prostoru valovne dolžine ali frekvence so določeni z Lahovo transformacijo kot:

${\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}$ ${\displaystyle ,}$ ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}(2)}$

Elementi matrike transformacije so Lahovi koeficienti: ${\displaystyle {\mathcal {A}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {1)!} }{\mathrm {(} m\mathrm {-} \mathrm {1)!} }}}$

Zgornji izraz, zapisan za GDD, pravi, da ima konstanta z valovno dolžino GGD nič višjih redov. Višji redi, ocenjeni iz GDD, so: ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}GDD\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}GDD\mathrm {(} \lambda \mathrm {)} }\end{array}}}$

Če enačbo (2), izraženo za lomni količnik ${\displaystyle n}$ ali optično pot ${\displaystyle OP}$, nadomestimo z enačbo (1), dobimo zaprte izraze za disperzijske redove. Na splošno je ${\displaystyle p^{th}}$ disperzijski red POD Laguerrova transformacija negativnega reda dva:

${\displaystyle POD={\frac {d^{p}\varphi (\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}OP(\lambda )}{d\lambda ^{m}}}}$ ${\displaystyle ,}$ ${\displaystyle POD={\frac {d^{p}k(\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}n(\lambda )}{d\lambda ^{m}}}}$

Matrični elementi transformacij so nepodpisani Laguerrovi koeficienti reda minus 2 in so podani kot: ${\displaystyle {\mathcal {B}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {2)!} }{\mathrm {(} m\mathrm {-} \mathrm {2)!} }}}$

Prvih deset disperzijskih redov, eksplicitno zapisanih za valovni vektor, je naslednjih:

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {GD}}}={\frac {\partial }{\partial \omega }}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \omega \mathrm {)} +\omega {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \lambda \mathrm {)} -\lambda {\frac {\partial n\mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\right)=v_{gr}^{\mathrm {-} \mathrm {1} }\end{array}}}$

Skupinski lomni količnik ${\displaystyle n_{g}}$ je definiran kot: ${\displaystyle n_{g}=cv_{gr}^{\mathrm {-} \mathrm {1} }}$.

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {GDD}}}={\frac {{\partial }^{2}}{\partial {\omega }^{\mathrm {2} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {2} {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}+\omega {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}\right)={\frac {\mathrm {1} }{c}}\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)\left({\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {TOD}}}={\frac {{\partial }^{3}}{\partial {\omega }^{\mathrm {3} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {3} {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}+\omega {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }{\Bigl (}\mathrm {3} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {FOD}}}={\frac {{\partial }^{4}}{\partial {\omega }^{\mathrm {4} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {4} {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}+\omega {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }{\Bigl (}\mathrm {12} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {8} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {FiOD}}}={\frac {{\partial }^{5}}{\partial {\omega }^{\mathrm {5} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {5} {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}+\omega {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {60} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {60} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {15} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {SiOD}}}={\frac {{\partial }^{6}}{\partial {\omega }^{\mathrm {6} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {6} {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}+\omega {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {360} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {480} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {180} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {24} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+{\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {SeOD}}}={\frac {{\partial }^{7}}{\partial {\omega }^{\mathrm {7} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {7} {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {6} }}}+\omega {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {2520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {2100} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {420} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {35} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {EOD}}}={\frac {{\partial }^{8}}{\partial {\omega }^{\mathrm {8} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {8} {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}+\omega {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {20160} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {40320} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {25200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {6720} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {840} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {48} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+{\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {NOD}}}={\frac {{\partial }^{9}}{\partial {\omega }^{\mathrm {9} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {9} {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}+\omega {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {181440} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {423360} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {317520} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {105840} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {17640} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {1512} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {63} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {TeOD}}}={\frac {{\partial }^{10}}{\partial {\omega }^{\mathrm {10} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {10} {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}+\omega {\frac {{\partial }^{10}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {1814400} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4838400} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4233600} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{1693440}{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\\+\mathrm {352800} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {40320} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {2520} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {80} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}$

Eksplicitno, zapisano za fazo ${\displaystyle \varphi }$, lahko prvih deset disperzijskih redov izrazimo kot funkcijo valovne dolžine z uporabo Lahove transformacije (enačba (2)) kot:

${\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}$ ${\displaystyle ,}$ ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}={-}\left({\frac {\mathrm {2} \pi c}{{\omega }^{\mathrm {2} }}}\right){\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \lambda }}={-}\left({\frac {{\lambda }^{\mathrm {2} }}{\mathrm {2} \pi c}}\right){\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{2}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}={\frac {\partial }{\partial \omega }}\left({\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }\left(\mathrm {2} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+{\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{3}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }\left(\mathrm {6} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {6} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{4}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {24} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {36} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{\mathrm {5} }\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {120} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {240} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {20} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{6}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {720} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1800} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {300} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {30} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}\mathrm {\ +} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{7}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {7} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {5040} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {15120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12600} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {630} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {42} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{8}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {40320} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {141120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {141120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {58800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {11760} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {1176} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {56} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\\+{\lambda }^{\mathrm {8} }{\frac {\partial ^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}$ ${\displaystyle {\begin{array}{l}{\frac {{\partial }^{9}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {362880} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1451520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1693440} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {846720} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {211680} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {28224} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {2016} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {72} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {\partial ^{\mathrm {9} }\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{10}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {10} }{\Bigl (}\mathrm {3628800} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {16329600} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {21772800} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {12700800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {3810240} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {635040} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {60480} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {3240} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {90} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}$

Glej tudi

• optična prizma
• disperzija v optičnem vlaknu