Lissajousova krivulja

Lissajousova krivulja (tudi Bowditchova krivulja) pripada družini krivulj, ki nastanejo zaradi harmonskega nihanja, ki izhaja iz dveh med seboj pravokotnih smeri.

To družino krivulj je proučeval že ameriški matematik Nathaniel Bowditch (1773 – 1838) v letu 1815 in pozneje še francoski matematik Jules Antoine Lissajous (1822 – 1880) v letu 1857.

Parametrična oblika Lissajousove krivulje

V parametrični obliki lahko zapišemo Lissajousovo krivuljo kot

${\displaystyle x=A\sin(at+\delta ),\quad y=B\sin(bt),}$.

kjer so

• ${\displaystyle a,b,A,B}$ izbrani
• ${\displaystyle \delta ,t}$ spremenljivi

Oblika krivulje je močno odvisna od razmerja ${\displaystyle a/b\,}$. Posebni primeri so: elipsa, če je razmerje enako 1, krožnica, če je ${\displaystyle A=B\,}$ in ${\displaystyle \delta =\pi /2}$ radianov in premica, če je ${\displaystyle \delta =0}$. Tudi parabola je Lissajousova krivulja, ki ima ${\displaystyle a/b=2}$ in ${\displaystyle \delta =\pi /2}$. Drugačna razmerja dajo bolj komplicirane krivulje, ki pa so zaprte samo, če je razmerje racionalno število.

Lissajousove krivulje, ki imajo ${\displaystyle a=1\,}$ in ${\displaystyle b=N\,}$ ter zanje velja

${\displaystyle \delta ={\frac {N-1}{N}}{\frac {\pi }{2}}\ }$, se imenujejo polinomi Čebišova prvega reda in N-te stopnje. N je naravno število.

Lissajousova krivulja na osciloskopu, kjer je prikazano razmerje 3:1 med vertikalno in horizontalno frekvenco sinusnega vhoda.

Zgledi

Spodnja animacija prikazuje spremembe krivulje za razstoče razmerje ${\displaystyle a/b\,}$ od 0 do 1 v korakih po 0,01. prikazana je animacija za ${\displaystyle \delta =0\,}$.

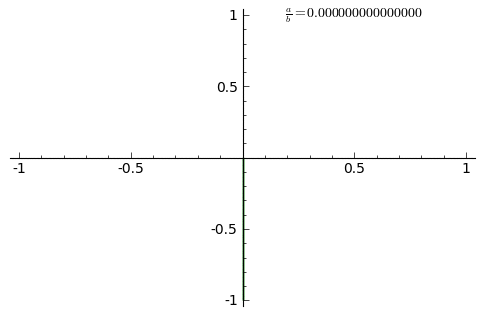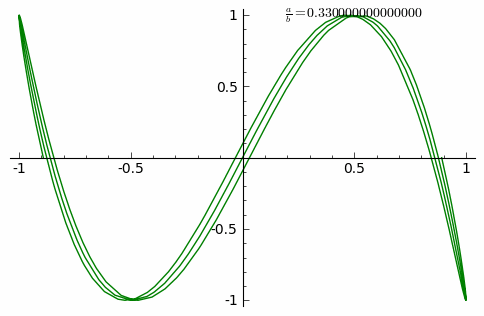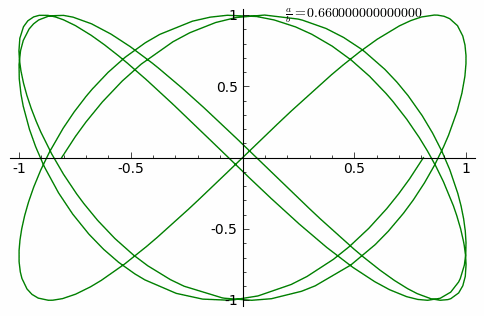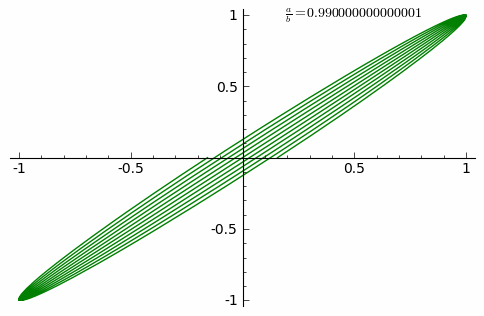
V spodnjih primerih je ${\displaystyle \delta =\pi /2\,}$, neparno naravno število a, parno naravno število b in ${\displaystyle |a-b|=1\,}$.

• 
  a = 1, b = 2 (1:2)
• 
  a = 3, b = 2 (3:2)
• 
  a = 3, b = 4 (3:4)
• 
  a = 5, b = 4 (5:4)
• 
  a = 5, b = 6 (5:6)
• 
  a = 9, b = 8 (9:8)

Glej tudi

• seznam krivulj
• Lissajousova tirnica
• Blackburnovo nihalo
• vrtnica (krivulja)

Zunanje povezave

• Lissajousova krivulja na MathWorld (angleško)
• Lissajousova krivulja na 2dcurves.com (angleško)
• Lissajousova krivulja na osciloskopu Arhivirano 2008-04-15 na Wayback Machine. (angleško)
• Animirana Lissajousova krivulja Arhivirano 2005-11-29 na Wayback Machine. (angleško)
• Animirani prikaz nastanka Lissajousove krivulje (angleško)
• Interaktivni aplet Arhivirano 2011-09-17 na Wayback Machine. (angleško)
• Interaktivni aplet (angleško)