Симпсоново правило

Симпсоново правило названо тако по Томасу Симпсону је метода из нумеричке анализе којом приближно израчунавамо одређен интеграл неке функције f(x), тј. интересује нас апроксимација ${\displaystyle \int _{a}^{b}f(x)dx}$.

Функцију f(x) (плава) апроксимирамо уз помоћ квадратне функције P(x) (црвена).

Идеја

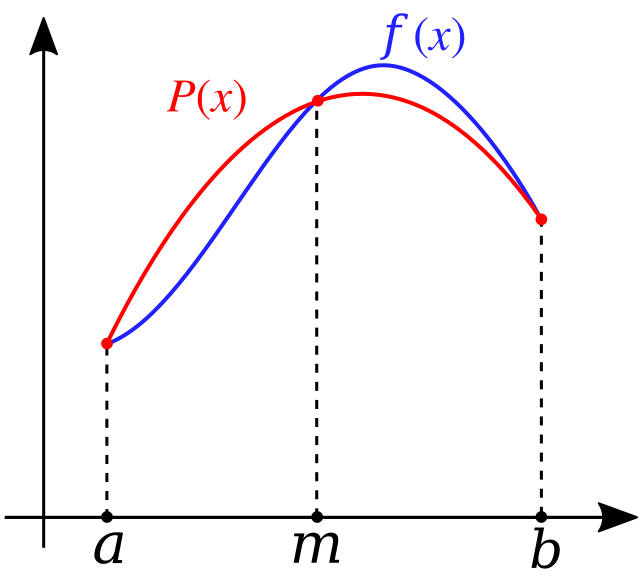
Симпсонова формула (или правило) је у ствари део Њутн-Коутс формула. Функцију прво апроксимирамо уз помоћ Лагранжових полинома другог степена, а после уместо да израчунамо интеграл функције ${\displaystyle f(x)}$, израчунавамо интеграл добијеног полинома:

${\displaystyle f(x)\approx P(x)=\sum _{i=0}^{n=2}l_{i}(x)\cdot f(x_{i})}$, притом

${\displaystyle l_{i}(x)=\prod _{j=0,j\neq i}^{n}{\frac {x-x_{j}}{x_{i}-x_{j}}}}$

Означимо почетну тачку интеграла ${\displaystyle a=x_{0}}$, крајњу ${\displaystyle b=x_{2}}$, а тачку у средини ${\displaystyle m=x_{1}}$ (обратити пажњу на скицу са стране) и добићемо:

${\displaystyle P(x)=f(a){\frac {(x-m)(x-b)}{(a-m)(a-b)}}+f(m){\frac {(x-a)(x-b)}{(m-a)(m-b)}}+f(b){\frac {(x-a)(x-m)}{(b-a)(b-m)}}\approx f(x)}$

Овом приликом није приказано како се долази до коначне формуле; рачун није тежак и састоји се од примене једноставних правила за интеграле (на пример, примена интеграла на суму):

${\displaystyle \int _{a}^{b}f(x)\,dx\approx \int _{a}^{b}P(x)\,dx={\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right]}$

Када се жели апроксимирати интеграл у интервалу од ${\displaystyle a}$ до ${\displaystyle b}$ тада ће за то бити неопходне три тачке дате функције.

Грешка у датом интервалу је:

${\displaystyle E_{S}=-{\frac {(b-a)^{5}}{90}}f^{(4)}(\xi )}$, где је ${\displaystyle \xi \in [a,b]}$.

Уколико желимо да нађемо највећу могућу грешку односно њену границу, довољно је максимирати четврти извод функције за ${\displaystyle \xi }$:

${\displaystyle \left|E_{S}\right|\leq {\frac {(b-a)^{5}}{90}}\left|\max _{a\leq \xi \leq b}f^{(4)}(\xi )\right|}$

Обзиром да грешка зависи од размака између тачака којима се врши апроксимација, а ако се означи тај размак са ${\displaystyle h={\frac {b-a}{2}}}$, може се рећи, користећи се O-нотацијом да се грешка налази ${\displaystyle E_{S}={\mathcal {O}}(h^{5})}$.

Сложено Симпсоново правило

Илустрација сложеног Симпсоновог правила.

Уколико смо незадовољни апроксимацијом, један од начина за побољшање је да интервал поделимо на више делова (мањих интервала) те да на сваком појединачно применимо Симпсоново правило и на крају их саберемо.

Означимо број тачака са ${\displaystyle n}$, а размак између њих са ${\displaystyle h={\frac {b-a}{n}}}$ и добићемо:

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+2\sum _{j=1}^{n/2-1}f(x_{2j})+4\sum _{j=1}^{n/2}f(x_{2j-1})+f(x_{n}){\bigg ]}}$,

што такође можемо написати као

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+4f(x_{1})+2f(x_{2})+4f(x_{3})+...+4f(x_{n-1})+f(x_{n}){\bigg ]}}$

или као производ вектора (${\displaystyle f=(f(x_{0}),f(x_{1}),\dots ,f(x_{n})}$ ):

${\displaystyle f\cdot (1,4,2,4,2,\dots ,2,4,1)^{T}}$.

Грешка за сложено Симпсоново правило је:

${\displaystyle \left|E_{S}\right|\leq {\frac {h^{4}}{180}}(b-a)\left|\max _{a\leq \xi \leq b}f^{(4)}(\xi )\right|}$

Такође, као што видимо, формулу за Симпсоново правило можемо извести и из комбинације трапезоидног правила и правила правоугаоника (${\displaystyle Q_{S}(f)}$ означава апроксимацију интеграла функције ${\displaystyle f}$ између датих ${\displaystyle a}$ и ${\displaystyle b}$, ${\displaystyle Q_{T}(f)}$ то исто за трапезоидно правило, а ${\displaystyle Q_{R}(f)}$ за правило правоугаоника):

${\displaystyle Q(f)={1 \over 3}(Q_{S}(f)+2Q_{T}(f))}$

Адаптивно Симпсоново правило

У пракси се понекад сусрећемо са ситуацијама када је нека функција у одређеним областима „досадна“ и чије интеграле можемо да израчунамо врло лако са мало тачака (када је функција релативно „испеглана"), док је у одређеним областима врло променљива и ту нам за добру апроксимацију треба много више тачака.

Да бисмо то постигли, користићемо се тактиком "подели па владај":

1. Израчунај средишну тачку датог интервала ${\displaystyle [a,b]}$: ${\displaystyle m={\frac {b-a}{2}}}$
2. Израчунај апроксимацију интеграла за ${\displaystyle [a,b]}$ користећи се Симпсоновим правилом (назовимо је ${\displaystyle S_{[a,b]}}$
3. Израчунај апроксимације за подељен интервал (означимо је ${\displaystyle S_{[a,m]}}$ и ${\displaystyle S_{[m,b]}}$) уз помоћ обичног Симпсоновог правила.
4. Уколико смо задовољни разликом ${\displaystyle S_{[a,b](S_{[a,m]}+S_{[m,b]})}$, резултат је ${\displaystyle S_{[a,m]}+S_{[m,b]}}$.
5. Уколико нисмо, наставимо даље рекурзивно примењујући адаптивно Симпсоново правило на интервале ${\displaystyle [a,m]}$ и ${\displaystyle [m,b]}$, а резултат је њихова сума.

Грешка адаптивног Симпсоновог правила

Обележимо резултат адаптивног Симпсоновог правила примењеног на интервалу ${\displaystyle [a,b]\,}$ за функцију ${\displaystyle f\,}$ са ${\displaystyle S(a,b)\,}$, a размак између двеју тачака са ${\displaystyle h={\frac {b-a}{2}}\,}$ онда важи:

За ${\displaystyle h\,}$: ${\displaystyle \int _{a}^{b}f(x)dx=S(a,b)-{\frac {h^{5}}{90}}\cdot f^{(4)}(\xi )-{\mathcal {O}}(h^{7})}$

За ${\displaystyle {\frac {h}{2}}}$: ${\displaystyle \int _{a}^{b}f(x)dx=S\left(a,{\frac {a+b}{2}}\right)+S\left({\frac {a+b}{2}},b\right)-\underbrace {2\cdot {\frac {(h/2)^{5}}{90}}} _{-{$Прекорачена је граница дубине језичког претварача (10)\frac {1}{16}}{\frac {h^{5}}{90}}}\cdot f^{(4)}({\tilde {\xi }})-{\mathcal {O}}(h^{7})}

Из тога даље закључујемо, под претпоставком ${\displaystyle f^{(4)}(\xi )=f^{(4)}({\tilde {\xi }})}$:

${\displaystyle S\left(a,{\frac {a+b}{2}}\right)+S\left({\frac {a+b}{2}},b\right)-{\frac {1}{16}}\left({\frac {h^{5}}{90}}\right)f^{(4)}(\xi )\approx S(a,b)-{\frac {h^{5}}{90}}f^{(4)}(\xi )}$

${\displaystyle \Rightarrow {\frac {h^{5}}{90}}f^{(4)}(\xi )\approx {\frac {16}{15}}\left(S(a,b)-S\left(a,{\frac {a+b}{2}}\right)-S\left({\frac {a+b}{2}},b\right)\right)}$

Тако можемо даље доћи до (разумно) приближне вредности грешке:

${\displaystyle \left|\int _{a}^{b}f(x)dx-S\left(a,{\frac {a+b}{2}}\right)-S\left({\frac {a+b}{2}},b\right)\right|\approx {\frac {1}{15}}\left|S(a,b)-S\left(a,{\frac {a+b}{2}}\right)-S\left({\frac {a+b}{2}},b\right)\right|}$

Ова приближна грешка је врло згодна као критеријум за крај рекурзије.

Спољашње везе

• Hazewinkel Michiel, ур. (2001). „Simpson formula”. Encyclopaedia of Mathematics. Springer. 978-1556080104.
• Weisstein, Eric W. „Simpson's Rule”. MathWorld.
• Application of Simpson's Rule — Earthwork Excavation (Note: The formula described in this page is correct but there are errors in the calculation which should give a result of 569m3 and not 623m3 as stated)
• Simpson's 1/3rd rule of integration — Notes, PPT, Mathcad, Matlab, Mathematica, Maple at Numerical Methods for STEM undergraduate
• A detailed description of a computer implementation is described by Dorai Sitaram in Teach Yourself Scheme in Fixnum Days, Appendix C