Инверзна функција

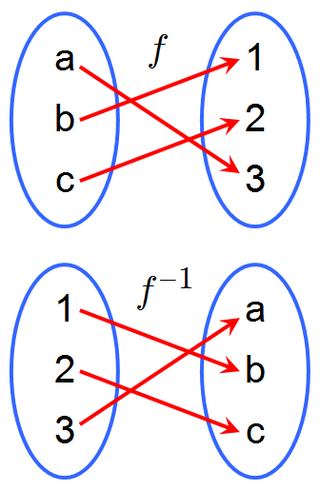
У математици, ако функција ƒ пресликава скуп на скуп , онда је њена инверзна функција ƒ^-1 таква да пресликава скуп на скуп и то тако да сложена функција ${\displaystyle f\circ f^{-1}}$ пресликава сваки елемент скупа на самог себе. Нема свака функција своју инверзну, она која има се зове инверзибилна.

Функција и њена инверзна ^–1. Како пресликава у 3, инверзна функција ^–1 пресликава 3 назад на .

Нпр., ако је дата функција ƒ таква да даје дужину у миљама ако је дата дужина у метрима (ƒ() = 1,6 · ), онда њена инверзна функција = ƒ^-1 даје дужину у метрима ако је позната дужина у миљама ( = / 1,6).

Инверзибилност

1. Како функција мора да пресликава оригинал у само једну слику, то функција која није инјективна не може имати инверзну.
2. С друге стране, ако се опсег функције није идентичан њеном кодомену, онда за неке елементе скупа-слике неће бити дефинисано пресликавање ƒ^-1.

Зато можемо рећи да је функција инверзибилна акко је бијекција.

• 
  Сурјективно али неинјективно пресликавање
• 
  Инјективно али несурјективно пресликавање
• 
  Бијекција

Нпр. функција ${\displaystyle f(x)=x^{2}:\mathbb {R} \rightarrow \mathbb {R} }$ није ни инјективна (јер позитивни и негативни бројеви имају исту слику), ни сурјективна (јер је ранг ${\displaystyle \mathbb {R} ^{+}}$, а не читав кодомен ${\displaystyle \mathbb {R} }$). Иста функција, али дефинисана као ${\displaystyle \mathbb {R} ^{+}\rightarrow \mathbb {R} ^{+}}$ има инверзну функцију ${\displaystyle {\sqrt {x}}}$. Функција ${\displaystyle f(x)=x^{3}\,\!}$ има инверзну, а ${\displaystyle f(x)=x^{3}-x\,\!}$ нема јер није инјективна (${\displaystyle f(0)=f(1)=0\,\!}$).

Особине

Симетрија

Нека је функција идентитета . Тада важи

${\displaystyle {\begin{aligned}f\circ f^{-1}=id_{X}\\f^{-1}\circ f=id_{Y}\end{aligned}}}$

односно ${\displaystyle (f^{-1})^{-1}=f\,\!}$.

Инверзна функција сложене функције

При инверзији композиције функција, основне функције мењају редослед:

${\displaystyle (f\circ g)^{-1}=g^{-1}\circ f^{-1}}$

Аутоинверзија

Функција идентитета је инверзна сама себи:

${\displaystyle id_{X}^{-1}=id_{X}\,\!}$

Графичко представљање

Функција и њена инверзна функција су симетричне у односу на праву ${\displaystyle y=x\,\!}$.

Извод инверзне функције

Ако је почетна функција диференцијабилна, онда се за све тачке у којима ${\displaystyle f(x)\neq 0\,\!}$ важи следећа формула за извод инверзне функције:

${\displaystyle {\frac {d}{dy}}\left[f^{-1}(y)\right]={\frac {1}{f'\left(f^{-1}(y)\right)}}.}$

Обележавање

Важно је уочити да ^-1 у означавању инверзне функције није ознака за експонент. Заправо ${\displaystyle {\tfrac {1}{f(x)}}}$ се записује као ƒ()^-1.

У инфинитезималном рачуну ознака ƒ⁽ⁿ⁾ означава -ти извод функције:

${\displaystyle f^{(n)}(x)={\frac {d^{n}}{dx^{n}}}f(x).}$

У тригонометрији, из историјских разлога, ${\displaystyle \sin ^{2}x=(\sin x)^{2}\,\!}$ а не ${\displaystyle \sin(\sin x)\,\!}$, али је ${\displaystyle \sin ^{-1}x=\arcsin x\,\!}$, а не ${\displaystyle {\tfrac {1}{\sin x}}}$. Управо да би се избегла ова непрецизност, за инверзне тригонометријске функције користи се ознака , а за реципрочне потпуно друга имена (${\displaystyle {\tfrac {1}{\sin x}}=\csc x}$). .

Литература

• Spivak, Michael (1994), Calculus (3rd изд.), Publish or Perish, ISBN 978-0-914098-89-8
• Stewart, James (2002), Calculus (5th изд.), Brooks Cole, ISBN 978-0534393397

Види још

• Теорија скупова
• Функција
• Списак инверзних функција
• Инјективно пресликавање
• Сурјективно пресликавање
• Бијективно пресликавање