Toppfrågor
Tidslinje
Chatt
Perspektiv
Geometri
matematisk lära Från Wikipedia, den fria encyklopedin
Remove ads
Geometri (grekiska: γεωμετρια geometria; av γεω geo ”jord”, och μετρια metria ”mäta”, det vill säga”lantmätarkonst”[1]) är en gren av matematiken där man studerar vilka egenskaper figurer har i ett rum eller, mer generellt, rumsliga samband.[1] Geometrin var en av de två ursprungliga matematiska disciplinerna, vid sidan av talteorin (studiet av talen).



I modern tid har geometrin generaliserats till en hög abstraktionsnivå och komplexitet. Många av dess grenar berörs idag av matematisk analys och abstrakt algebra och kan vara mycket svåra att känna igen som ättlingar till den tidigaste geometrin. Beroende på vilka axiom man utgår ifrån får man olika geometrier, det vill säga geometriska teorier.
Remove ads
Historia
Sammanfatta
Perspektiv

Den allra äldsta bevarade geometrin, som kommer från det gamla Egypten och Babylonien (Mesopotamien[1]) med början omkring 3 000 f.Kr.,[2][3] var en samling empiriskt härledda principer om längd, vinklar, ytor och volymer, som man utvecklat för att tillfredsställa de praktiska behov som uppstått ur lantmäteri, konstruktion, astronomi och olika hantverk. Flera av dessa principer var förvånansvärt sofistikerade, och dagens matematiker kan ha svårt att härleda dem utan att använda matematisk analys. Till exempel kände både egyptierna och babylonierna till Pythagoras sats omkring 1 500 år före Pythagoras. Egyptierna kunde korrekt beräkna volymen på en stympad pyramid med kvadratisk bas och babylonierna hade trigonometriska tabeller.[4][5][6]
I Kina hade man med största sannolikhet kommit lika långt inom matematiken.
Den grekiska perioden (600 f.Kr.–600 e.Kr.)
Grekerna utvecklade från och med 600-talet f.Kr.[1] geometrin till att omfatta många nya figurer, kurvor, ytor och kroppar. De ersatte tidigare induktiva metoder med logiska, deduktiva, och de insåg att geometrin studerar abstrakta, ideala former. De upptäckte även det axiomatiska system som under mer än 2 000 år betraktats som det ideala paradigmet för alla vetenskapliga teorier.
Thales skrev deduktiva bevis för fem geometriska satser, men dessa bevis är försvunna.[7] Pythagoras upptäckte inte den sats som idag bär hans namn, men han var den förste som kunde presentera ett deduktivt bevis för den.[8][9][10] Pythagoréerna och hans lärjungar studerade matematik, musik och filosofi, och tillsammans utforskade de det mesta av den geometri som idag studeras på gymnasiet. Dessutom upptäckte man, till sin egen förtvivlan, inkommensurabla sträckor och därmed de irrationella talen.
Matematiker accepterade Platons övertygelse att geometrin uteslutande skulle använda sig av passare och en ograderad linjal och aldrig någon form av mätverktyg, gradskiva eller något annat verktyg som man förknippade med praktiskt hantverk. Detta maxim gjorde att man fördjupade sig i konstruktioner med passare och linjal och dess tre klassiska konstruktionsproblem: kubens fördubbling, vinkelns tredelning och cirkelns kvadratur. De bevisades omöjliga i dessa konstruktioner först på 1800-talet. Aristoteles skrev en traktat om metodisk argumentation i deduktiva bevis, en metodlära som förblev oförändrad ända fram till 1800-talet.
Euklides skrev Geometrins elementa, en axiomatisk beskrivning av geometrin.[11][12] Detta var det första systematiska arbetet byggt på axiom och författat cirka år 300 f.Kr.[1] Även Eudoxos var ett viktigt namn i utvecklingen av den tidiga grekiska geometrin.[1]
Det grekiska utvecklandet av geometrin fick dock en nedgång efter cirka 200 f.Kr., efter författandet av verk av Apollonios från Perga samt banbrytande verk av Arkimedes.[1] Den sistnämnde utvecklade metoder som starkt påminner om den analytiska geometrins koordinatsystem och integralkalkylens[1] approximationer. Det enda som saknades för att han skulle kunna skapa dessa matematiska discipliner var verkningsfulla algebraiska beteckningar som kunde uttrycka hans idéer.[13]
Medeltiden, renässansen och reformationen
Den islamiska dominansen i Mellanöstern, Nordafrika och Spanien inleddes omkring 640 e.Kr. Biblioteket i Alexandria brändes ned av kristna vid 300-talet. De första framstående persiska matematikerna ägnade sig mer åt algebra än geometri, även om exempelvis poeten och geometrikern Omar Khayyam bidrog med viktiga kommentarer till ämnet.[14][15] I Europa förföll matematiken till den grad att till och med de klassiska verken gick förlorade där och bara överlevde via de islamiska lärdomscentrerna.[16]
Under medeltidens slut studerades de klassiska grekiska och romerska verken i islamiska bibliotek och översattes från arabiska till latin. Man återupptäckte Euklides Elementa och geometrins deduktiva metoder återerövrades. Utvecklingen av geometrin i enlighet med Euklides metoder återupptogs, och ett stort antal viktiga och till och med eleganta satser och begrepp tillkom.
1600-talet och början av 1700-talet
Descartes och Fermat introducerade analytisk geometri med koordinater och ekvationer. Desargues studerade projektiv geometri utan användning av måttenheter, egenskaper som inte påverkas av projektion (till exempel hur punkter relaterar sig till varandra).
I slutet av 1600-talet utvecklade, oberoende av varandra, Newton (1642–1727) och Leibniz (1646–1716) differentialkalkylen. Det blev början på ett helt ny gren inom matematiken som idag kallas analys; denna gjorde det enkelt att hitta tangenten till godtyckliga kurvor och att finna arean hos en yta som omsluts av sådana kurvor.
Parallellpostulatets fall
Saccheri (1667–1733[1]), Lambert (1728–1777[1]) och Legendre gjorde under 1700-talet var och en för sig viktiga upptäckter kring detta bevis för Euklides parallellpostulat, men ingen av dem lyckades hitta lösningen. I början av 1800-talet valde Gauss, Bolyai och Lobatjevskij en annan väg.[1] Oberoende av varandra drog de slutsatsen att det var omöjligt att bevisa parallellpostulatet, och de började istället utveckla en icke-euklidisk geometri där postulatet var falskt. 1854 presenterade Riemann, som studerat för Gauss, ett banbrytande arbete där han visade hur differentialkalkylen kunde appliceras på rum med godtyckligt antal dimensioner, det vill säga en fristående geometri som var giltig för alla släta ytor.
Eugenio Beltrami bevisade 1868[1] att den icke-euklidiska geometrin var fristående. En lång och noggrann undersökning hade till sist uppdagat logiska brister i Euklides resonemang och outtalade antaganden som hans argumentation vilade på. Samtidigt drabbades differentialkalkylen och den numeriska analysen av en kris sedan man misslyckats med att hantera betydelsen av oändliga processer som konvergens och kontinuitet.
I geometrin fanns ett påtagligt behov av en ny uppsättning postulat som var helt oklanderliga och stod helt oberoende av bilder på ett papper och vår intuitiva bild av ett rum. David Hilbert presenterade 1899[1] en ny uppsättning geometriska axiom. Hans axiom anslöt sig till Euklides diton och har fått betydelse i modern pedagogik genom ett överbryggande mellan euklidisk och icke-euklidisk geometri.[1]
Remove ads
Grundläggande begrepp
Sammanfatta
Perspektiv
Några grundläggande begrepp inom geometrin är:
Punkt
En punkt betecknar inom geometri ett objekt utan någon utsträckning. För att ange en punkts läge används koordinater. Antalet koordinater som behövs för att ange punktens läge bestäms av dimensionen.
Linje

En linje är en utsträckning i rummet med en dimension. Det innebär att läget för en punkt på linjen bestäms av en koordinat, vilket är det samma som ett matematiskt tal. Med linje menar man oftast en rät linje, men det kan generellt sett vara vilken kurva som helst.
Plan
Ett plan är en utsträckning i rummet med två dimensioner; en rät linje som förbinder två punkter på ytan ligger därför till hela sin längd i på ytan (i planet). En punkts läge i ett plan bestäms alltså av två koordinater, och koordinaterna anger punktens läge i förhållande till ett koordinatsystem. En yta är också tvådimensionell och utgör en yttre begränsning av en kropp, eller en avgränsning mellan två kroppar.
Kropp
En kropp är ett objekt i tre dimensioner. Volymen är ett mått på kroppens innehåll.
Symmetri
Ett annat grundläggande begrepp inom geometri är symmetri. Inom geometrin avser man med symmetri oftast spegelsymmetri, vilket innebär att ett föremål är identiskt med spegelbilden av ett annat föremål i något plan.
Remove ads
Geometriska former
Några av de allra vanligaste geometriska objekten är:
- Kvadrat – består av fyra hörn på 90 grader och fyra lika långa sidor. Arean är samma som sidlängden gånger två. Diagonalerna halverar varandra.
- Rektangel – består av fyra hörn på 90 grader. Area = längd x höjd. Diagonalerna halverar varandra.
- Cirkel – en oändlig mängd punkter med samma avstånd från en central punkt. Area = pi × radie².
Grenar
Sammanfatta
Perspektiv
Det finns flera grenar inom geometrin, bland annat:
Analytisk geometri
Analytisk geometri är en gren av geometrin där algebraiska metoder från främst linjär algebra används för att lösa geometriska problem.
Metoder från analytisk geometri används inom alla tillämpade vetenskaper, men särskilt inom fysiken som för att beskriva planeternas banor. Ursprungligen behandlade analytisk geometri endast frågor rörande planet och den rumsliga (euklidiska) geometrin. Mera allmänt beskriver den analytiska geometrin affina rum av godtyckliga dimensioner över godtyckliga kroppar.
Euklidisk geometri

Inom euklidisk geometri gäller Euklides fem axiom, av vilka ett är det så kallade parallellaxiomet. De geometriska teorier som inte bygger på parallellaxiomet kallas icke-euklidiska geometrier.
De olika teorierna ger olika sanningsvärden för vissa geometriska påståenden. Inom euklidisk geometri är det till exempel sant att vinkelsumman i en triangel alltid är 180 grader, vilket inte är fallet i icke-euklidisk geometri.
Den euklidiska geometrin är den konventionella form av geometri som lärs ut i skolorna, då den har otaliga praktiska tillämpningar. Man kan grovt göra följande uppdelning:
- beräkningar med vinklar (trigonometri)
- kägelsnitt, inklusive
Icke-euklidisk geometri
En icke-euklidisk geometri är en geometrisk teori där Euklides femte axiom, det så kallade parallellaxiomet, inte gäller. Både hyperbolisk och elliptisk geometri (den senare inkluderar exempelvis sfärisk geometri[1]) är icke-euklidiska, och de står därmed i kontrast till euklidisk geometri. Den hyperboliska geometrin utvecklades under första halvan av 1800-talet, av namn som Gauss, Bolyai och inte minst Lobatjevskij (se ovan).[1] Bolyai kallade sin teori för absolut geometri.[1]
Den väsentliga skillnaden mellan euklidisk och icke-euklidisk geometri är de parallella linjernas natur. Inom euklidisk geometri kan vi, om vi utgår från en punkt A och en linje l, dra endast en linje genom A som är parallell med l. Inom hyperbolisk geometri finns det å andra sidan oändligt många linjer genom A parallella med l, och inom elliptisk geometri existerar inte parallella linjer.
Ett annat sätt att beskriva skillnaderna mellan dessa geometrier är som följande: betrakta två linjer i ett plan som båda är vinkelräta mot en tredje linje. Inom euklidisk och hyperbolisk geometri är då de två linjerna parallella. Inom euklidisk geometri förblir emellertid de två linjerna på ett konstant avstånd från varandra, medan de inom hyperbolisk geometri "böjer av" från varandra med ökande avstånd i takt med att avståndet från skärningspunkten med den gemensamma vinkelräta linjen ökar. Inom elliptisk geometri "kröker" linjerna mot varandra, och slutligen skär de varandra; således existerar inga parallella linjer inom elliptisk geometri.

Beteende hos linjer med gemensam ortogonal linje i vardera av de tre sorternas geometri.[17]
Differentialgeometri
Differentialgeometri är studier av differentierbara mångfalder, det vill säga topologiska rum som lokalt ser ut som en öppen delmängd i . Detta möjliggör nyttjandet av metoder från matematisk analys.
Den har många tillämpningar inom fysiken, särskilt inom relativitetsteorin. Centralt hos differentialgeometrin är studiet av riemannska mångfalder (se även riemanngeometri). Dessa är geometriska objekt som exempelvis ytor som lokalt liknar ett euklidiskt rum och därför medger definition av analytiska koncept som tangentvektorer, tangentrum, differentierbarhet, vektorfält och tensorfält.
Dessa mångfalder är utrustade med metrik. Detta tillåter geometri därför att de medger mätning av distans och vinkel lokalt och definierar koncept som geodeter, krökning och torsion.
Topologi
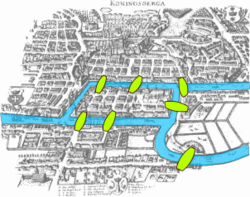
Topologi är en form av geometri där endast formen på objekten, och inte några avstånd, betraktas.
En topologi beskriver ett antal volymers fysiska form och formen på deras gemensamma rum såsom de gemensamma resulterande öppningarna och överbryggningarna. En topologisk beskrivning kan till exempel vara ett schema över hållplatserna för kollektivtrafiken i en stad som inte tar hänsyn till avstånden. Topologi är viktigt för att avgöra logistik då man adderar anläggningar av industrikomplex i flera plan och i många byggnader. Topologi används också då man anlägger datanätverk på ett kontor och väljer hur datorerna skall kopplas samman i förhållande till varandra i nätverk.
Topologin föddes i början av 1900-talet och är därför ett relativt nytt område inom matematiken. Den har visat sig mycket användbar och tillämpas numera inom andra grenar av matematiken såsom analys och algebra, såväl som inom andra vetenskaper som till exempel fysik och genetik.
I geografiska databaser är topologi en förutsättning för att kunna göra vissa GIS-analyser. Detta kan gälla närmaste väg mellan två noder eller se vilka objekt som finns intill varandra.
Topologin generaliserar begreppen kontinuerlig funktion och öppen mängd. Den introduceras ofta genom att först definiera "topologiska rum", sedan "kontinuerliga funktioner" mellan dessa rum. Därefter studerar man olika "topologiska egenskaper" hos dessa.
Algebraisk geometri
Algebraisk geometri är en gren inom matematiken som kan sägas vara en kombination av linjär algebra och algebra.[18] Här studeras geometriska strukturer till ekvationer med en eller flera variabler. Man vill alltså, med hjälp av algebraiska ekvationer, kunna definiera kurvor och ytor. Eftersom det inte alltid går att få fram ett exakt svar är man, inom algebraisk geometri, mer intresserad av att förstå strukturen på geometrin av systemet av ekvationer än av lösningen.[19]
Remove ads
Referenser
Externa länkar
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

