சார்பின் வரைபடம்

கணிதத்தில் f என்ற சார்பின் வரைபடம் (graph of a function) என்பது வரிசைச் சோடிகள் (x, f(x) அனைத்தின் தொகுப்பாகும். சார்பின் ஆட்களத்தின் உறுப்புகள் மெய்யெண்களின் வரிசைப்படுத்தப்பட்ட சோடிகளாக (x₁, x₂) என இருக்குமானால், அச்சார்பின் வரைபடம் (x₁, x₂, f(x₁, x₂)) இன் தொகுப்பாக அமையும். தொடர்ச்சியான சார்பிற்கு இவ்வரைபடம் முப்பரிமாண மேற்பரப்பாகும்.

f(x) = x⁴ − 4^x

(−2, +2) சார்பின் வரைபடம்.

x ஒரு மெய்யெண்ணாகவும் f ஒரு மெய்மதிப்புச் சார்பாகவும் இருந்தால் அச் சார்பின் வரைபடம் என்பதை அதன் வரைபட விளக்கமாகவும் (கார்ட்டீசியன் தளத்திலமைந்த ஒரு வளைவரையாக) மற்ற சார்புகளுக்கு முறையான வரையறையையும் கொள்ளலாம்.

வெவ்வேறான இணையாட்களங்களைக் கொண்ட இரு சார்புகளுக்கு ஒரே வரைபடம் இருக்கலாம் என்பதால் ஒரு சார்பு அதன் வரைபடத்தால் அடையாளங் காணப்பட்டாலும் அவை இரண்டும் ஒன்றாக முடியாது. எடுத்துக்காட்டாக ஒரு முப்படிக் கோவையின் இணையாட்களம் மெய்யெண்களின் கணமாக இருப்பின் அச்சார்பு ஒரு உள்ளிடு கோப்பாக அமையும்; இணையாட்களம் சிக்கலெண் களமாக இருப்பின் உள்ளிடு கோப்பாக இருக்காது.

கார்ட்டீசியன் தளத்தில் அமைந்த ஒரு வளைவரையின் வரைபடம் x இன் சார்பாக இருக்குமா என்பதைக் குத்துக்கோட்டுச் சோதனை மூலமும், y இன் சார்பாக இருக்குமா என்பதை கிடைக்கோட்டுச் சோதனை மூலமும் அறியலாம். ஒரு சார்புக்கு நேர்மாறுச் சார்பு இருந்தால், தரப்பட்டச் சார்பின் வரைபடத்தை y = x கோட்டில் பிரதிபலிப்பதன் மூலம் நேர்மாறுச் சார்பின் வரைபடத்தைப் பெறமுடியும்.

எடுத்துக்காட்டுகள்

f(x) = x³ − 9x சார்பின் வரைபடம்.

ஒருமாறியிலமைந்த சார்புகள்

${\displaystyle f(x)=\left\{{\begin{matrix}a,&{\mbox{if }}x=1\\d,&{\mbox{if }}x=2\\c,&{\mbox{if }}x=3.\end{matrix}}\right.}$ சார்பின் வரைபடம்:

{(1,a), (2,d), (3,c)}.

மெய்யெண் கோட்டின் மீது முப்படிக் கோவையின் வரைபடம்:

முப்படிச் சார்பு:

${\displaystyle f(x)=x^{3}-9x}$

வரைபடம்:

{(x, x³ − 9x) : x ஒரு மெய்யெண்}.

இவற்றை கார்ட்டீசியன் தளத்தில் குறித்தால் படத்திலுள்ள வளைவரை கிடைக்கும்.

இருமாறியிலமைந்த சார்புகள்

f(x, y) = sin(x²) · cos(y²) சார்பின் வரைபடம்.

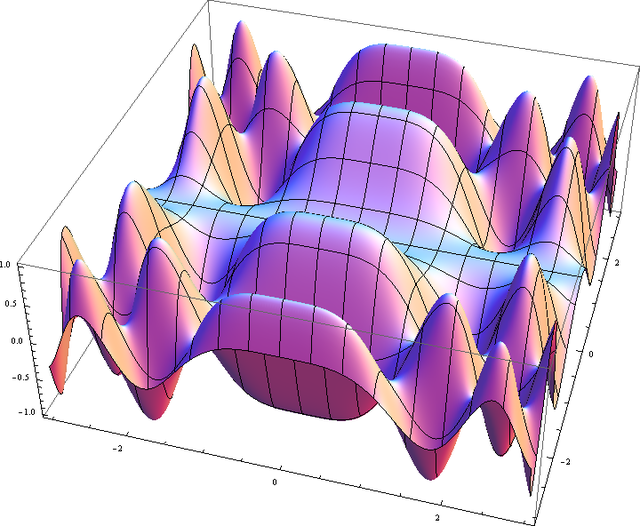
முக்கோணவியல் சார்பின் வரைபடம் (மெய்யெண்கோட்டின் மீது):

சார்பு:

f(x, y) = sin(x²) · cos(y²)

வரைபடம்:

{(x, y, sin(x²) · cos(y²)) : x , y மெய்யெண்கள்}.

இவற்றை முப்பரிமாணக் கார்ட்டீசியன் தளத்தில் குறித்தால் படத்திலுள்ளவாறு ஒரு மேற்பரப்பு கிடைக்கும்.

வெளி இணைப்புகள்

விக்கிமீடியா பொதுவகத்தில்,
Graphs
என்பதில் ஊடகங்கள் உள்ளன.

• Interactive function graph plotter
• Graph of function, derivative and antiderivative plotter பரணிடப்பட்டது 2016-03-18 at the வந்தவழி இயந்திரம்
• Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.