படிக்குறிச் சார்பு

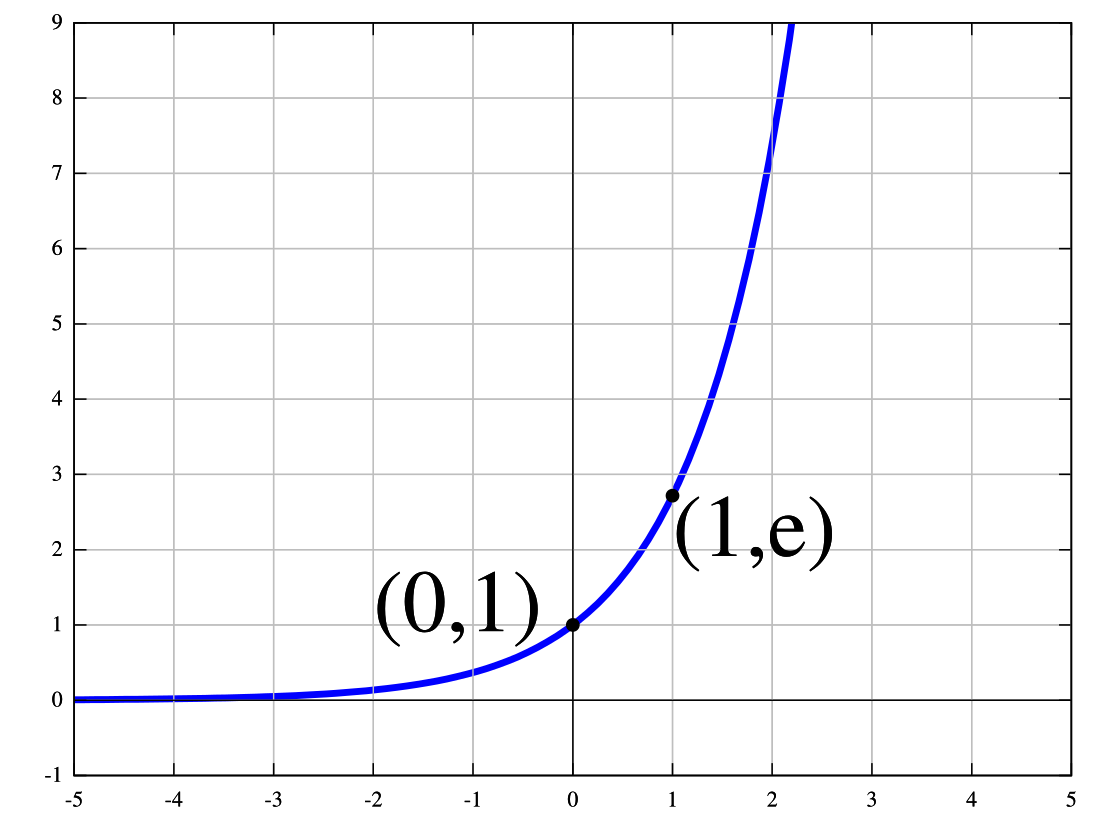
கணிதத்தில் படிக்குறிச் சார்பு அல்லது அடுக்குக்குறிச் சார்பு (exponential function) என்பது, f(x) = e^x சார்பு ஆகும். இதிலுள்ள கணித மாறிலி e தோராயமாக 2.718281828 மதிப்புடையது. e^x இன் வகைக்கெழுவும் e^x.^[1][2]

-

குறியீடு	${\displaystyle e^{x}\,}$
நேர்மாறு	${\displaystyle \ln x\,}$
வகைக்கெழு	${\displaystyle e^{x}\,}$
வரையறாத் தொகையீடு	${\displaystyle e^{x}+C\,}$

இயல் படிக்குறிச் சார்பு ${\displaystyle y=e^{x}}$ இன் வரைபடம்.

y = e^x சார்பின் வரைபடம் மேல்நோக்குச் சாய்வு கொண்டது; வரைபடத்தில் x இன் மதிப்பு அதிகரிக்க அதிகரிக்க, அதற்குரிய y மதிப்பு வேகமாக அதிகரிக்கிறது. வரைபடம் எப்பொழுதும் x-அச்சுக்கு மேற்புறமாகவும் x இன் எதிர் மதிப்புகளுக்கு x-அச்சை ஒட்டினாற்போலும் அமைகிறது. எனவே x-அச்சு இந்த வரைபடத்திற்கு கிடைமட்ட அணுகுகோடாகும். வரைபடத்தின் மேலமையும் ஒவ்வொரு புள்ளியிலும் வளைவரையின் சாய்வு அப்புள்ளியின் y ஆயதொலைவுக்குச் சமம். படிக்குறிச் சார்பின் நேர்மாறுச் சார்பு இயல் மடக்கை ln(x) ஆகும். இதனால் சில கணித புத்தகங்கள் படிக்குறிச் சார்பை எதிர்மடக்கை என்றும் குறிப்பிடப்படுகின்றன^[3].

சில சமயங்களில் படிக்குறிச் சார்பு என்பது பொதுவாக cb^x ( b ஒரு மெய்யெண்) என்ற வடிவச் சார்புகளுக்குப் பயன்படுத்தப்படுகிறது.

மாறி x மெய்யெண்ணாகவோ, சிக்கலெண்ணாகவோ அல்லது வேறெந்தவொரு கணிதப் பொருளாகவும் இருக்கலாம்.

வரையறை

படிக்குறிச் சார்பு (நீலம்); அடுக்குத் தொடரின் (இடப்புறம்) முதல் n + 1 உறுப்புகளின் கூடுதல் (சிவப்பு)

படிக்குறிச் சார்பு e^x, பல சமான வழிகளில் வரையறுக்கப்படுகிறது.

• அடுக்குத் தொடராக வரையறுத்தல்:^[4].

${\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }$

டெயிலரின் தொடராக விரிக்கும் போதும் இதே விளைவு கிடைக்கும்.

• ${\displaystyle x=\int _{1}^{y}{dt \over t}}$ என்ற தொகையீட்டுச் சமன்பாட்டின் தீர்வு y ஆக வரையறுக்கப்படுகிறது.
• ${\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}}$ என, முடிவிலி எல்லை மதிப்பாக வரையறுக்கப்படுகிறது.

கண்ணோட்டம்

ஒரு கணியம் அதன் தற்போதைய மதிப்பின் விகிதத்தில் வளரும் (சிதையும்) போதும் படிக்குறிச் சார்பு உருவாகிறது. தொடர்ச்சியான கூட்டு வட்டி கணக்கிடுவது இதற்கு ஒரு எடுத்துக்காட்டாகும்

தற்போது e என்றறியப்படும் ${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}$ என்ற எண், 1683 ஆம் ஆண்டு கணிதவியலாளர் ஜேக்கப் பெர்னோலியால் கண்டறியப்பட இதுவே காரணமாக இருந்தது. ^[5] பின்னர் 1697 இல் ஜோகன் பெர்னோலி, படிக்குறிச் சார்பின் நுண்கணிதம் குறித்து ஆய்வு செய்தார்^[5].

மாதந்தோறும் கூட்டுவட்டி கணக்கிடப்படும் திட்டத்தில் அசல் தொகை 1, ஆண்டு வட்டி வீதம் x எனில் ஒவ்வொரு மாதமும் கிடைக்கும் வட்டியின் மதிப்பு அதன் நடப்பு மதிப்பில் x/12 மடங்காகும். எனவே ஒவ்வொரு மாதமும் மொத்த மதிப்பானது (1+x/12) காரணியால் பெருக்கப்பட்டு ஆண்டின் இறுதியில் கிடைக்கும் மதிப்பு (1+x/12)¹² ஆக இருக்கும். இதுபோல நாள்தோறும் வட்டி கணக்கிடப்பட்டால் ஆண்டின் இறுதியில் கிடைக்கும் மதிப்பாக (1+x/365)³⁶⁵ இருக்கும். ஓர் ஆண்டில் வட்டி கணக்கிடப்படும் இடைவெளிகளின் எண்ணிக்கை வரம்பின்றி அதிகரிக்கப்படும்போது படிக்குறிச் சார்பின் வரையறை முடிவிலி எல்லையாகக் கிடைக்கிறது:

${\displaystyle \exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}$

படிக்குறிச் சார்பின் இவ்வரையறை முதன்முதலாக ஆய்லரால் கண்டறியப்பட்டது^[6]

படிக்குறிச் சார்பின் பிற வரையறைகள் தொடர்களையும் வகையீட்டுச் சமன்பாடுகளையும் கொண்டுள்ளன.

எல்லாவகை வரையறைகளிலும் படிக்குறிச் சார்பானது

${\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y)}$

என்ற அடுக்கேற்றத்தின் அடிப்படை விதியை நிறைவு செய்வதைக் காணலாம். இதனாலேயே இச்சார்பு e^x என எழுதப்படுகிறது.

வகைக்கெழுக்களும் வகையீட்டுச் சமன்பாடுகளும்

படிக்குறிச் சார்பின் வகைக்கெழு படிக்குறிச் சார்பின் மதிப்பாகவே இருக்கும். வளைவரை (நீலம்) மீதுள்ள ஒரு புள்ளி ${\displaystyle P}$ இல் வளைவரைக்கு ஒரு தொடுகோடு (சிவப்பு), ${\displaystyle h}$ அளவு உயரம் கொண்ட ஒரு நிலைக்குத்துக் கோடு ((பச்சை), ${\displaystyle x}$-அச்சு மூன்றும் சேர்ந்து ${\displaystyle b}$ அளவு அடிப்பக்கம் கொண்ட ஒரு செங்கோண முக்கோணத்தை உருவாக்குகின்றன. தொடுகோட்டின் சாய்வு (${\displaystyle {\frac {h}{b}}.}$) இது வளைவரையின் வகைக்கெழு ஆகும். ஆனால் படிக்குறிச் சார்பின் வகைக்கெழு அச்சார்பின் மதிப்பாகவே (${\displaystyle h}$)இருக்கும் என்ற உண்மையின்படி ${\displaystyle {\frac {h}{b}}=h.}$ எனவே ${\displaystyle b=1}$ ஆகி விடுகிறது. அதாவது அடிப்பக்கம் ${\displaystyle b}$ எப்பொழுதும் ${\displaystyle 1}$ ஆகவே இருக்கும்.

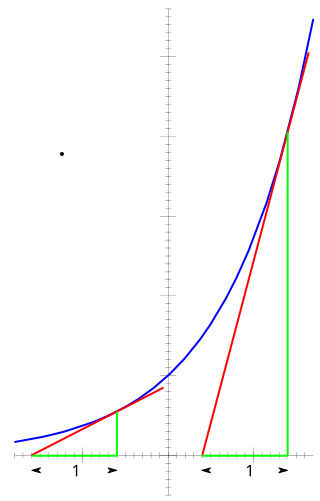
படிக்குறிச் சார்பு அதன் வகைக்கெழுவின் பண்புகளால் முக்கியமானதொரு சார்பாக உள்ளது. இச் சார்பின் வகைக்கெழு:

${\displaystyle {\operatorname {d} \over \operatorname {d} x}e^{x}=e^{x}}$

அதாவது e^x இன் வகைக்கெழு e^x ஆகும். இதிலிருந்து பின்வரும் கூற்றுகளைக் காணலாம்:

• சார்பின் வளைவரையின் மேலுள்ள எந்தவொரு புள்ளியிடத்தும் சார்பின் சாய்வு, அப்புள்ளியில் சார்பின் மதிப்பிற்குச் சமம்.
• x இல் சார்பின் மாறுவீதம் அதே x இல் சார்பின் மதிப்பிற்குச் சமம்.
• y ′ = y என்ற வகையீட்டுச் சமன்பாட்டின் தீர்வாக e^x அமையும்.

ஒரு மாறி x இன் வளரும் (சிதையும்) வீதம் அதன் மதிப்பின் விகிதத்தில் அமையுமானால், அதனை நேரத்தில் (t) அமைந்த படிக்குறிச் சார்பின் ஒரு மாறிலி மடங்காக, அதாவது ce^kt என எழுதலாம். இதில் k , c மெய்யெண் மாறிலிகள். அதாவது, f(x) = ce^kx (c ஒரு மாறிலி) என இருந்தால், இருந்தால் மட்டுமே, சார்பு f: R→R, f′ = kf (k ஒரு மாறிலி) என்பதை நிறைவு செய்யும்.

மேலும் வகையிடலின் சங்கிலி விதிப்படி வகையிடக்கூடிய எந்தவொரு சார்பு f(x) க்கும் கீழ்வரும் கூற்று உண்மையாகும்:

${\displaystyle {\operatorname {d} \over \operatorname {d} x}e^{f(x)}=f'(x)e^{f(x)}}$

ex இல்- தொடரும் பின்னங்கள்

ஆயிலரின் முற்றொருமை மூலம் e^x இற்கான தொடரும் பின்னத்தைக் காணமுடியும்:

${\displaystyle e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-{\cfrac {4x}{x+5-{\cfrac {5x}{x+6-\ddots }}}}}}}}}}}}}$

பின்வரும் e^x இற்கான பொதுமைப்படுத்தப்பட்ட தொடரும் பின்னம் வேகமாக ஒருங்குகிறது:^[7]

${\displaystyle e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+{\cfrac {z^{2}}{18+{\cfrac {z^{2}}{22+{\cfrac {z^{2}}{26+\ddots }}}}}}}}}}}}}}}$

இதில் z = ^x⁄_y எனப் பிரதியிட:

${\displaystyle e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+{\cfrac {x^{2}}{18y+{\cfrac {x^{2}}{22y+{\cfrac {x^{2}}{26y+\ddots }}}}}}}}}}}}}}}$

z = 2 எனும் சிறப்புவகை:

${\displaystyle e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}}$

z > 2 எனில் இது மெதுவாக ஒருங்குகிறது. எடுத்துக்காட்டாக:

${\displaystyle e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}}$

சிக்கலெண் தளத்தில்

சிக்கலெண் தளத்தில் படிக்குறிச் சார்பு. அழுத்தமான நிறத்திலிருந்து மெலிதான நிறத்திற்கு மாறுவதிலிருந்து படிக்குறிச் சார்பின் அளவு வலப்புறமாகக் கூடுகிறது என்பதை அறிந்து கொள்ளலாம். காலமுறை கிடைமட்டப் பட்டைகள், படிக்குறிச் சார்பு காலமுறைச் சார்பு என்பதைக் காட்டுகிறது.

மெய்யெண்களில் வரையறுக்கப்பட்டது போல படிக்குறிச் சார்பைச் சிக்கலெண் தளத்திலும் சமானமான பல வடிவங்ககளில் வரையறுக்கலாம். சிக்கலெண் படிக்குறிச் சார்பு காலமுறைச் சார்பாகும். இதன் காலமுறை அளவு ${\displaystyle 2\pi i.}$

• அடுக்குத் தொடர் மூலமான வரையறையில் மெய்யெண் மாறிக்குப் பதில் சிக்கலெண் மாறியைப் பிரதியிட, படிக்குறிச் சார்பு:

${\displaystyle e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}}$

சிக்கலெண் ${\displaystyle z=a+bi}$ எனில்

${\displaystyle e^{a+bi}=e^{a}(\cos b+i\sin b)}$

இதில் a , b இரண்டும் மெய்யெண்கள்^[8] இந்த வாய்ப்பாடு படிக்குறிச் சார்பினை முக்கோணவியல் சார்புகளுடனும் அதிபரவளையச் சார்புகளுடனும் இணைக்கிறது.

பண்புகள்: அனைத்து சிக்கலெண்கள் z , w இற்கும்:

• ${\displaystyle e^{z+w}=e^{z}e^{w}\,}$
• ${\displaystyle e^{0}=1\,}$
• ${\displaystyle e^{z}\neq 0}$
• ${\displaystyle {\operatorname {d} \over \operatorname {d} z}e^{z}=e^{z}}$
• ${\displaystyle \,(e^{z})^{n}=e^{nz},n\in \mathbb {Z} }$

இயல் மடக்கையை சிக்கலெண்களுக்கு நீட்டிக்கக் கிடைப்பது log z எனும் சிக்கலெண் மடக்கை. இது ஒரு பன்மதிப்புச் சார்பு.

சிக்கலெண் தளத்திலுள்ள எந்தவொரு கோட்டிற்கும் படிக்குறிச் சார்பின் சார்பலன் சிக்கலெண் தளத்திலமையும் மடக்கைச் சுருளாக இருக்கும். இச்சுருளின் மையம் ஆதிப்புள்ளி. இதன் இரு சிறப்பு வகைகள்: கோடு மெய் அச்சுக்கு இணையாக இருந்தால் அதன் எதிருரு தன்மீது முடிவடையா சுருளாகவும், கோடு கற்பனை அச்சுக்கு இணையாக இருந்தால் அதன் எதிருருவான சுருள் வட்டமாகவும் இருக்கும்.

• 
  z = Re(e^x+iy)
• 
  z = Im(e^x+iy)
•