Переріз Дедекінда

Переріз Дедекінда — це конструкція з математичного аналізу, запропонована Ріхардом Дедекіндом, за допомогою якої надається математично строге визначення дійсних чисел.

Визначення

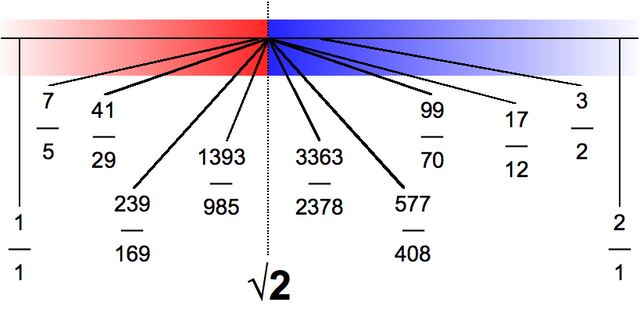
Переріз Дедекінда — це розбиття множини усіх раціональних чисел ${\displaystyle \mathbb {Q} }$ на дві непорожні підмножини A та B із властивостями, що A не має найбільшого елемента і будь-яке число з множини A менше від будь-кого числа з множини B. Множина A називається нижнім класом перерізу, а множина B — верхнім класом перерізу.

Будь-яке раціональне число x призводить до переріза Дедекінда, у якому

${\displaystyle A=\{a\in \mathbb {Q} :a<x\},\quad B=\{b\in \mathbb {Q} :b\geq x\}.}$

Оскільки множина B повністю визначена множиною A, а саме, B = Q\A, визначення переріза Дедекінда часто надається в термінах нижнього класу. Таким чином, переріз Дедекінда — це множина A раціональних чисел із властивостями:

• A непорожня, ${\displaystyle A\neq \emptyset$ ;}
• А не становить всю множину раціональних чисел, ${\displaystyle A\neq \mathbb {Q}$ ;}
• А замкнута знизу, тобто якщо ${\displaystyle a\in A}$ та ${\displaystyle ~c<a,}$ то ${\displaystyle c\in A;}$
• А не має найбільшого елемента, тобто для будь-якого ${\displaystyle a\in A}$ знайдеться ${\displaystyle c\in A,c>a.}$

Перерізи Дедекінда утворюють множину R, на якій можуть бути визначені операції додавання та множення, а також поняття порядку. Таким чином множина R перетворюється на упорядковане поле дійсних чисел. Якщо у верхньому класі є найменше число, то такий переріз відповідає раціональному числу, у супротивному випадку — ірраціональному числу.

Приклади

Дійсному числу ${\displaystyle {\sqrt {2}}}$ відповідає наступний дедекіндовий переріз: ${\displaystyle A=\{a\in \mathbb {Q} :a\leqslant 0\lor a^{2}<2\}}$ та ${\displaystyle B=\{b\in \mathbb {Q} :b>0\land b^{2}\geqslant 2\}\,}$. Інтуїтивно можна представити, що для визначення ${\displaystyle {\sqrt {2}}}$, ми розділили множину раціональних чисел на дві частини: всі числа, що лівіше ${\displaystyle {\sqrt {2}}}$, та всі числа, що правіше ${\displaystyle {\sqrt {2}}}$; тобто, ${\displaystyle {\sqrt {2}}}$ є точною нижньою гранню множини ${\displaystyle ~B.}$

Див. також

• Аксіома Дедекінда

Джерела

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)
• Ляшко І.І., Ємельянов В.Ф., Боярчук О.К. Математичний аналіз. Частина 1. — К. : Вища школа, 1992. — 496 с. — ISBN 5-11-003757-4.(укр.)
• Александров П.С. Введение в теорию множеств и общую топологию. — Москва : Наука, 1977. — 368 с. — ISBN 5354008220.(рос.)