Рівняння Фрідмана

Рівняння Фрідмана — система диференційних рівнянь у фізичній космології, які описують розширення Всесвіту в однорідних та ізотропних моделях Всесвіту в межах загальної теорії відносності. Їх уперше вивів Олександр Фрідман у 1922 році з рівнянь Ейнштейна для метрики Фрідмана — Леметра — Робертсона — Вокера і ідеальної рідини з заданою густиною ρ та тиском p^[1]. Рівняння для випадку від'ємної просторової кривини були подані Фрідманом у 1924 році^[2]. Фізичні моделі, побудовані на основі рівнянь Фрідмана, лежать в основі сучасної космології її стандартної моделі ΛCDM.

Рівняння Фрідмана мають вигляд:

${\displaystyle H^{2}=\left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}}$

${\displaystyle {\dot {H}}+H^{2}={\frac {\ddot {a}}{a}}=-{\frac {4\pi G}{3}}\left(\rho +{\frac {3p}{c^{2}}}\right)+{\frac {\Lambda c^{2}}{3}}}$

Тут H - параметр Габбла, a - космологічний масштабний фактор, G - гравітаційна стала, ${\displaystyle \Lambda }$ - космологічна стала, ${\displaystyle \rho }$ - густина речовини, p - тиск, c - швидкість світла, k = 1, 0, -1 для замкненого, евклідового та відкритого Всесвіту відповідно. В цих рівняннях від часу залежать масштабний фактор a, густина речовини ${\displaystyle \rho }$ та тиск p, а також параметр Габбла ${\displaystyle H}$.

Припущення

Докладніше: Метрика Фрідмана — Леметра — Робертсона — Вокера

Рівняння Фрідмана ґрунтуються на трьох основних припущеннях^[3]:22.1.3:

1. Метрика Фрідмана — Леметра — Робертсона — Вокера,
2. Рівняння Ейнштейна для загальної теорії відносності,
3. Всесвіт заповнений ідеальною рідиною.

Метрика, у свою чергу, спирається на спрощувальне припущення, що Всесвіт є просторово однорідним і ізотропним, тобто відповідає космологічному принципу. Емпірично це підтверджується на масштабах, більших за приблизно 100 Мпк.

Метричний тензор можна записати так^[4]:65:

$${\displaystyle c^{2}d\tau ^{2}=c^{2}dt^{2}-R^{2}(t)\left(dr^{2}+S_{k}^{2}(r)d\psi ^{2}\right)}$$

де$${\displaystyle S_{-1}(r)=\sinh(r),\quad S_{0}(r)=r,\quad S_{1}(r)=\sin(r).}$$

Ці три варіанти відповідають значенням параметра k: (0) — плоский простір, (+1) — сфера сталої додатної кривини, (−1) — гіперболічний простір сталої від’ємної кривини.

Тут радіальну координату подано через масштабний фактор, що залежить від часу, ${\displaystyle R(t)}$, і співрухому координату ${\displaystyle r}$. Підставляння цього метричного тензора в рівняння поля Ейнштейна дає співвідношення між еволюцією масштабного фактора та тиском й енергією речовини у Всесвіті. Використовуючи тензор енергії-імпульсу для ідеальної рідини, отримують рівняння, наведені нижче^[4]:73.

Рівняння

Існують два незалежні рівняння Фрідмана, що описують однорідний та ізотропний Всесвіт. Перше має вигляд^[3]:

$${\displaystyle H^{2}\equiv {\left({\frac {\dot {R}}{R}}\right)}^{2}={\frac {8\pi G\rho }{3}}-{\frac {k}{R^{2}}}+{\frac {\Lambda }{3}},}$$

а друге:

$${\displaystyle {\frac {\ddot {R}}{R}}={\frac {\Lambda }{3}}-{\frac {4\pi G}{3}}\left(\rho +3p\right).}$$

Термін «рівняння Фрідмана» іноді застосовують лише до першого рівняння^[3].

У цих рівняннях H — параметр Габбла, R(t) — космологічний масштабний фактор, ${\displaystyle G}$ — гравітаційна стала Ньютона, Λ — космологічна стала з розмірністю довжина⁻², ρ — густина енергії, а p — ізотропний тиск. Величина k є сталою в межах окремого розв’язку, але може відрізнятися між різними розв’язками. У вибраній системі одиниць швидкість світла у вакуумі прийнята рівною одиниці.

У наведених рівняннях R, ρ та p є функціями часу. Якщо знехтувати космологічною сталою Λ, то член ${\displaystyle -k/R^{2}}$ у першому рівнянні Фрідмана можна інтерпретувати як ньютонівську повну енергію, отже, еволюція Всесвіту є «змаганням» між гравітаційною потенціальною енергією ${\displaystyle 8\pi G\rho /3}$ та кінетичною енергією ${\displaystyle {\dot {R}}/R}$. Результат залежить від значення k у повній енергії: якщо k = +1, гравітація зрештою призводить до стискання Всесвіту. Ці висновки змінюються, якщо Λ ≠ 0^[3].

Використовуючи перше рівняння, друге можна переписати у вигляді^[3]:

$${\displaystyle {\dot {\rho }}=-3H\left(\rho +{\frac {p}{c^{2}}}\right),}$$

що дозволяє виключити Λ. Як альтернативу, той самий результат можна отримати із закону збереження маси-енергії^[3]:

$${\displaystyle T^{\alpha \beta }{}_{;\beta }=0}$$Перше рівняння Фрідмана містить дискретний параметр k = +1, 0 або −1, що відповідає випадкам, коли форма Всесвіту є замкненою (3-сфера), плоскою (евклідів простір) або відкритою (тривимірний гіперболоїд), відповідно^[5]. Якщо k додатне, то Всесвіт є «замкненим»: рухаючись певним шляхом, можна повернутися у початкову точку. Такий Всесвіт подібний до сфери — скінченний, але безмежний. Якщо k від’ємне, то Всесвіт є «відкритим» — нескінченним, і жоден шлях не повертається у вихідну точку. Якщо ж k = 0, то Всесвіт є евклідовим (плоским) і нескінченним^[4]:69.

Безрозмірний масштабний фактор

Безрозмірний масштабний фактор можна визначити як:$${\displaystyle a(t)\equiv {\frac {R(t)}{R_{0}}},}$$де ${\displaystyle R_{0}=R(t={\text{нині}})}$.

Рівняння Фрідмана можна записати через цей безрозмірний масштабний фактор наступним чином:$${\displaystyle H^{2}(t)=\left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\left[\rho (t)+{\frac {\rho _{c}-\rho _{0}}{a^{2}(t)}}\right],}$$де ${\displaystyle {\dot {a}}=da/dt}$, ${\displaystyle \rho _{c}=3H_{0}^{2}/8\pi G}$, а ${\displaystyle \rho _{0}=\rho (t={\text{нині}})}$^[6]:3.

Критична густина

Значення густини маси-енергії ${\displaystyle \rho }$, при якому ${\displaystyle k=0}$ та ${\displaystyle \Lambda =0}$, називається критичною густиною:$${\displaystyle \rho _{c}\equiv {\frac {3H^{2}}{8\pi G}}.}$$

Якщо густина Всесвіту більша, тобто ${\displaystyle \rho \geq \rho _{c}}$, то Всесвіт є просторово замкненим: у цьому спрощеному наближенні Всесвіт із часом почне стискатися. Якщо ж густина менша, ${\displaystyle \rho \leq \rho _{c}}$, то Всесвіт є просторово відкритим і розширюватиметься вічно. Таким чином, геометрія Всесвіту безпосередньо пов’язана з його густиною^[4]:73.

Параметр густини

Приблизна оцінка відносного розподілу компонентів густини енергії у Всесвіті. Темна енергія є домінантною енергетичною компонентою (74%), а темна матерія (22%) складає більшість маси. Лише 4% загальної маси припадає на баріонну матерію^[a].

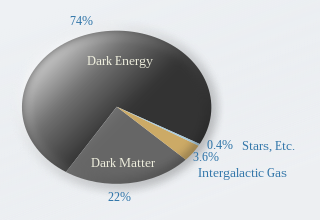
Параметр густини Ω визначають як відношення фактичної (спостережуваної) густини ρ до критичної густини ρ_c у рівняннях Фрідмана^[4]:74:$${\displaystyle \Omega$$ :={\frac {\rho }{\rho _{c}}}={\frac {8\pi G\rho }{3H^{2}}}.} Як густина ${\displaystyle \rho (t)}$, так і параметр Габбла ${\displaystyle H(t)}$ залежать від часу, тому параметр густини також змінюється з часом^[4]:74.

Критична густина еквівалентна приблизно п’яти атомам водню на кубічний метр, тоді як середня густина звичайної матерії у Всесвіті, за оцінками, становить 0,2–0,25 атома на кубічний метр^[7][8].

Значно більша частка густини припадає на невідому темну матерію, хоча як звичайна, так і темна матерія сприяють гравітаційному стисканню Всесвіту. Водночас найбільший внесок походить від так званої темної енергії, що відповідає члену з космологічною сталою. Попри те, що загальна густина дорівнює критичній (з точністю до похибки вимірювань), темна енергія не сприяє стисканню Всесвіту, а навпаки — може прискорювати його розширення.

Вираз для критичної густини отримують, якщо прийняти Λ рівною нулю (як у базових моделях Фрідмана) та покласти нормалізовану просторову кривину ${\displaystyle k}$ рівною 0. Підставивши ці значення у перше рівняння Фрідмана з використанням сучасного значення ${\displaystyle H_{0}}$, отримаємо^[9]:

$${\displaystyle {\begin{aligned}\rho ={\frac {3H_{0}^{2}}{8\pi G}}&\approx 1.10\times 10^{-26}\mathrm {kg\,m^{-3}} \\&\approx 1.88\times 10^{-26}{\rm {h}}^{2}\,{\rm {kg}}\,{\rm {m}}^{-3}\\&\approx 2.78\times 10^{11}h^{2}M_{\odot }\,{\rm {Mpc}}^{-3}\end{aligned}}}$$

де:

• ${\textstyle H_{0}=76.5\pm 2.2\,\mathrm {km\,s^{-1}\,Mpc^{-1}} \approx 2.48\times 10^{-18}\mathrm {s^{-1}} }$
• ${\textstyle h={\frac {H_{0}}{100\,\mathrm {(km/s)/Mpc} }}}$
• ${\displaystyle \rho _{c}=8.5\times 10^{-27}\mathrm {kg/m^{3}} }$

Просторову кривину та енергію вакууму також можна включити до більш загального виразу для Ω, у якому цей параметр густини точно дорівнює одиниці. Тоді завдання полягає у вимірюванні окремих компонент, що зазвичай позначаються індексами. Згідно з моделлю ΛCDM, головними складовими Ω є внески баріонів, холодної темної матерії та темної енергії.

За даними різних космологічних тестів кривина Всесвіту виявляється майже плоскою. Це означає, що Всесвіт можна добре наблизити моделлю з нульовим параметром просторової кривини k.

Перше рівняння Фрідмана часто записують через теперішні значення параметрів густини^[10]:$${\displaystyle {\frac {H^{2}}{H_{0}^{2}}}=\Omega _{0,\mathrm {R} }a^{-4}+\Omega _{0,\mathrm {M} }a^{-3}+\Omega _{0,k}a^{-2}+\Omega _{0,\Lambda }.}$$

Тут Ω_0,R — теперішнє значення густини випромінювання (за умови a = 1), Ω_0,M — густини матерії (як темної, так і баріонної), Ω_0,k = 1 − Ω₀ — «густини просторової кривини», а Ω_0,Λ — густини, пов’язана з космологічною сталою або енергією вакууму.

Моделі Фрідмана — Леметра — Робертсона — Вокера

Релятивістські космологічні моделі, що базуються на метриці Фрідмана — Леметра — Робертсона — Вокера і задовольняють рівнянням Фрідмана, називають моделями Фрідмана — Робертсона — Вокера^[4]:73. Безпосередні спостереження швидкостей галактик показали, що вони переважно визначаються радіальним розбіганням, що підтверджує ці припущення для космологічних моделей^[4]:65. Такі моделі становлять основу стандартної космологічної моделі^[11], включно з сучасною моделлю ΛCDM^[3].

Щоб застосувати цю метрику до космології та передбачити її часову еволюцію через масштабний фактор ${\displaystyle a(t)}$, використовують рівняння Ейнштейна разом із виразом для густини ${\displaystyle \rho (t)}$, який задається, наприклад, через космологічне рівняння стану^[en]. Ця процедура дозволяє отримати наближений аналітичний розв’язок рівнянь Ейнштейна ${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }=\kappa T_{\mu \nu }}$, який у випадку ізотропного й однорідного тензора енергії-імпульсу приводить до рівнянь Фрідмана^[12]:

$${\displaystyle {\begin{aligned}{\left({\frac {\dot {a}}{a}}\right)}^{2}+{\frac {kc^{2}}{a^{2}}}-{\frac {\Lambda c^{2}}{3}}&={\frac {\kappa c^{4}}{3}}\rho \\[4pt]2{\frac {\ddot {a}}{a}}+{\left({\frac {\dot {a}}{a}}\right)}^{2}+{\frac {kc^{2}}{a^{2}}}-\Lambda c^{2}&=-\kappa c^{2}p.\end{aligned}}}$$

Оскільки модель Фрідмана — Леметра — Робертсона — Вокера передбачає однорідність, у деяких популярних викладах хибно стверджується, що модель Великого вибуху не може пояснити спостережувану «згрудженість» Всесвіту. У строго ФЛРВ-моделі не існує галактичних скупчень чи зір, оскільки це області, густина яких набагато перевищує середню густину Всесвіту. Попри це, модель ФЛРВ використовується як перше наближення для опису еволюції реального, неоднорідного Всесвіту, оскільки вона відносно проста для розрахунків, а моделі, що враховують «згрудженість», розглядаються як розширення ФЛРВ-підходу. Більшість космологів погоджуються, що спостережуваний Всесвіт добре описується «майже ФЛРВ-моделлю» — тобто моделлю, яка відповідає метриці ФЛРВ з урахуванням лише первинних флуктуацій густини^[en]. Станом на Станом на 2003, теоретичні наслідки різних розширень моделі ФЛРВ вважаються добре зрозумілими, а головною метою є узгодження цих моделей зі спостереженнями, отриманими місіями COBE та WMAP.

Інтерпретація

Пара наведених вище рівнянь еквівалентна такій парі:$${\displaystyle {\begin{aligned}{\dot {\rho }}&=-3{\frac {\dot {a}}{a}}\left(\rho +{\frac {p}{c^{2}}}\right)\\[1ex]{\frac {\ddot {a}}{a}}&=-{\frac {\kappa c^{4}}{6}}\left(\rho +{\frac {3p}{c^{2}}}\right)+{\frac {\Lambda c^{2}}{3}}\end{aligned}}}$$де ${\displaystyle k}$ — показник просторової кривизни, який виступає сталою інтнгрування для першого рівняння.

Перше рівняння можна також отримати з термодинамічних міркувань; воно еквівалентне першому закону термодинаміки, якщо припустити, що розширення Всесвіту є адіабатичним процесом (це припущення неявно використовується під час виведення метрики Фрідмана — Леметра — Робертсона — Вокера).

Друге рівняння показує, що як густина енергії, так і тиск зумовлюють зменшення швидкості розширення Всесвіту ${\displaystyle {\dot {a}}}$, тобто призводять до його уповільнення. Це є наслідком гравітації, причому тиск відіграє роль, подібну до ролі густини енергії (або маси) згідно з принципами загальної теорії відносності. Космологічна стала, навпаки, спричиняє прискорення розширення Всесвіту.

Космологічна стала

Член із космологічною сталою можна опустити, якщо зробити такі заміни:$${\displaystyle {\begin{aligned}\rho &\to \rho -{\frac {\Lambda }{\kappa c^{2}}},&p&\to p+{\frac {\Lambda }{\kappa }}.\end{aligned}}}$$

Отже, космологічна стала може інтерпретуватися як форма енергії з негативним тиском, рівним за модулем її (додатній) густині мас-енергії: $${\displaystyle p=-\rho c^{2}\,,}$$що є рівняння стану вакууму з темною енергією.

Якщо спробувати узагальнити це до виразу $${\displaystyle p=w\rho c^{2}\,,}$$такий запис не матиме загальної коваріантності без додаткових модифікацій.

Насправді, щоб отримати член, який спричиняє прискорення розширення Всесвіту, достатньо наявності скалярного поля, що задовольняє умову $${\displaystyle p<-{\frac {\rho c^{2}}{3}}.}$$Таке поле іноді називають квінтесенцією.

Моделі пилу

Якщо в рівняннях Фрідмана покласти тиск ідеальної рідини рівним нулю (${\displaystyle p=0}$), отримаємо космологічну модель пилу^[13]:231.

Ньютонівська аналогія

У 1934 році Маккрі та Мілн^[14] показали, що рівняння Фрідмана у випадку безтискової рідини можна отримати, використовуючи нерелятивістську ньютонівську динаміку^[13]:231.

$${\displaystyle {\begin{aligned}-a^{3}{\dot {\rho }}=3a^{2}{\dot {a}}\rho +{\frac {3a^{2}p{\dot {a}}}{c^{2}}}\,,\\[1ex]{\frac {{\dot {a}}^{2}}{2}}-{\frac {\kappa c^{4}a^{3}\rho }{6a}}=-{\frac {kc^{2}}{2}}\,.\end{aligned}}}$$

Перше рівняння стверджує, що зменшення маси, яка міститься у фіксованому кубі (з миттєвою стороною a), дорівнює кількості маси, що залишає цей об’єм через його поверхню внаслідок розширення Всесвіту, плюс масовий еквівалент роботи, виконаної тиском проти речовини, яка виходить назовні. Це — вираз закону збереження маси-енергії (перший закон термодинаміки), застосований до частини Всесвіту.

Друге рівняння показує, що кінетична енергія (відносно початку координат) частинки одиничної маси, яка рухається разом із розширенням, плюс її (негативна) гравітаційна потенціальна енергія (відносно маси, що міститься у сфері ближче до центру), дорівнює сталому значенню, пов’язаному з кривиною Всесвіту. Інакше кажучи, енергія (відносно початку координат) співрухомої частинки, що вільно падає, зберігається. Загальна теорія відносності лише встановлює зв’язок між просторовою кривиною Всесвіту та енергією такої частинки: додатна повна енергія відповідає негативній кривині, а від’ємна повна енергія — позитивній кривині.

Корисні розв’язки

Рівняння Фрідмана можна розв’язати точно для ідеальної рідини з рівнянням стану$${\displaystyle p=w\rho c^{2},}$$де p — це тиск, ρ — густина рідини у співрухомій системі відліку, а w — деяка стала.

У випадку плоского Всесвіту (k = 0) розв’язок для масштабного фактора має вигляд$${\displaystyle a(t)=a_{0}\,t^{\frac {2}{3(w+1)}}\,,}$$де a₀ — стала інтегрування, яка визначається початковими умовами. Це сімейство розв’язків, параметризоване значенням w, має велике значення для космології. Наприклад, w = 0 описує епоху домінування матерії, коли тиск є незначним порівняно з густиною. Із загального розв’язку видно, що у Всесвіті, де домінує матерія, масштабний фактор змінюється як$${\displaystyle a(t)\propto t^{2/3}\qquad {\text{(домінування матерії)}}}$$

Інший важливий приклад — епоха домінування випромінювання, тобто коли w = 1/3. У цьому випадку маємо$${\displaystyle a(t)\propto t^{1/2}\qquad {\text{(домінування випромінювання)}}}$$

Слід зазначити, що цей розв’язок не застосовний для випадку домінування космологічної сталої, яке відповідає w = −1. Тоді густина енергії залишається сталою, а масштабний фактор зростає експоненційно.

Розв’язки для інших значень k наведено у джерелі: Tersic, Balsa. Lecture Notes on Astrophysics. Процитовано 24 лютого 2022.

Суміші

Якщо речовина складається з двох або більше невзаємодіючих рідин, кожна з яких описується таким рівнянням стану, то для кожної компоненти f виконується$${\displaystyle {\dot {\rho }}{f}=-3H\left(\rho {f}+{\frac {p_{f}}{c^{2}}}\right)\,.}$$У кожному випадку це можна записати як$${\displaystyle {\dot {\rho }}{f}=-3H\left(\rho {f}+w_{f}\rho _{f}\right)\,,}$$звідки випливає$${\displaystyle {\rho }{f}\propto a^{-3\left(1+w{f}\right)}\,.}$$

Наприклад, можна записати лінійну комбінацію таких членів:$${\displaystyle \rho =Aa^{-3}+Ba^{-4}+Ca^{0}\,,}$$де A — густина «пилу» (звичайної матерії, w = 0) при a = 1; B — густина випромінювання (w = 1/3) при a = 1; а C — густина темної енергії (w = −1).

Підставивши це у вираз$${\displaystyle \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}}$$можна отримати a як функцію часу.

Історія

Олександр Фрідман

Фрідман опублікував дві праці з космології у 1922–1923 роках. Він виходив із тих самих припущень про однорідність і ізотропність, які використовували у своїх роботах 1917 року Альберт Ейнштейн і Віллем де Сіттер. І Ейнштейн, і де Сіттер припускали, що Всесвіт є статичним, тобто незмінним у часі. Щоб забезпечити цю статичність, Ейнштейн додав до своїх рівнянь загальної теорії відносності додатковий член. У своїй статті де Сіттер показав, що простір-час має кривину навіть за відсутності матерії: нові рівняння загальної теорії відносності передбачали, що навіть вакуум має властивості, які змінюють структуру простору-часу^[15]:152.

Ідея статичного Всесвіту тривалий час була основоположною як у філософії, так і в науці. Проте Фрідман відмовився від цього припущення у своїй першій праці «Про кривину простору». Він почав з десяти рівнянь Ейнштейна, застосував симетрію ізотропного Всесвіту та просту модель для густинии мас-енергії й вивів співвідношення між цією густиною та кривиною простору-часу. Він показав, що крім одного статичного розв’язку, існує багато розв’язків, які залежать від часу^[15]:157.

Друга праця Фрідмана — «Про можливість світу з постійною від’ємною кривиною», опублікована 1924 року, — досліджувала складніші геометричні ідеї. У ній він показав, що з самих лише рівнянь загальної теорії відносності не можна вивести скінченність простору-часу: розв’язкам цих рівнянь можуть відповідати як скінченні, так і нескінченні геометрії. Фрідман навів аналогію з двома поняттями тривимірної сфери: подорож уздовж кола сталої широти може повернутися до початкової точки, або ж сфера може мати нескінченну кількість «аркушів», і тоді така подорож ніколи не повторюється^[15]:167.

Праці Фрідмана спочатку залишилися майже непоміченими, за винятком реакції самого Ейнштейна, який спершу їх відкинув. Однак після того як Едвін Габбл опублікував астрономічні свідчення розширення Всесвіту, Ейнштейн визнав правильність цих висновків. Жорж Леметр незалежно ввід Фрідмана відкрив деякі аспекти тих самих розв’язків і переконливо обґрунтував ідею Всесвіту, що виник із «первісного атому». Тому історики вважають обох учених в рівній мірі засновниками сучасної космології^[16].

Примітки

1. У лютому 2015 року команда науковців, що опрацьовувала результати, згенеровані космічним телескопом «Планк», опублікувала більш точні цифри: 4,9% звичайної матерії, 25,9% темної матерії і 69,1% темної енергії.