Список груп сферичної симетрії

Групи сферичної симетрії також називають точковими групами в тривимірному просторі, однак у цій статті розглянуто тільки скінченні симетрії. Існує п'ять фундаментальних класів симетрії, притаманних трикутним фундаментальним областям: діедрична, циклічна, тетраедрична, октаедрична^[en] та ікосаедрична симетрія.

Точкова група в тривимірному просторі

Симетрії-інволюції Cs, (*) [ ] =	Циклічна симетрія Cnv, (*nn) [n] =	Діедрична симетрія Dnh, (*n22) [n,2] =
Групи многогранників, [n,3], (*n32)
Тетраедрична симетрія Td, (*332) [3,3] =	Октаедрична симетрія Oh, (*432) [4,3] =	Ікосаедрична симетрія Ih, (*532) [5,3] =

В статті перелічено групи згідно з символами Шенфліса, нотацією Коксетера^[en][1], орбіфолдною нотацією^[en][2] і порядком. Конвей використовував варіант запису Шенфліса, заснований на алгебраїчній структурі групи кватерніонів, з позначеннями однією або двома великими літерами і повним набором нижніх числових індексів. Порядок групи позначається індексом, якщо тільки він не подвоюється символом плюс-мінус («±»), який передбачає центральну симетрію ^[3].

Також наведено символіку Германа — Могена (міжнародна нотація). Групи кристалографії, загалом 32, є підмножиною з елементами порядку 2, 3, 4 і 6^[4].

Симетрії-інволюції

Є чотири симетрії, які є оберненими собі, тобто інволюціями: тотожне перетворення (C₁), дзеркальна симетрія (C_s), обертова симетрія (C₂), і центральна симетрія (C_i).

Міжн.	Геом. [5]	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
1	1	11	C1	C1	][ [ ]+	1
2	2	22	D1 = C2	D2 = C2	[2]+	2

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
1	22	×	Ci = S2	CC2	[2+,2+]	2
2 = m	1	*	Cs = C1v = C1h	±C1 = CD2	[ ]	2

Циклічна симетрія

Існують чотири нескінченних сімейства циклічної симетрії^[en] з n=2 і вище (n може дорівнювати 1 як особливий випадок немає симетрії).

Міжн.	Гео	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
2	2	22	C2 = D1	C2 = D2	[2]+ [2,1]+	2
mm2	2	*22	C2v = D1h	CD4 = DD4	[2] [2,1]	4
4	42	2×	S4	CC4	[2+,4+]	4
2/m	22	2*	C2h = D1d	±C2 = ±D2	[2,2+] [2+,2]	4

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
3 4 5 6 n	3 4 5 6 n	33 44 55 66 nn	C3 C4 C5 C6 Cn	C3 C4 C5 C6 Cn	[3]+ [4]+ [5]+ [6]+ [n]+	3 4 5 6 n
3m 4mm 5m 6mm -	3 4 5 6 n	*33 *44 *55 *66 *nn	C3v C4v C5v C6v Cnv	CD6 CD8 CD10 CD12 CD2n	[3] [4] [5] [6] [n]	6 8 10 12 2n
3 8 5 12 -	62 82 10.2 12.2 2n.2	3× 4× 5× 6× n×	S6 S8 S10 S12 S2n	±C3 CC8 ±C5 CC12 CC2n / ±Cn	[2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+]	6 8 10 12 2n
3/m=6 4/m 5/m=10 6/m n/m	32 42 52 62 n2	3* 4* 5* 6* n*	C3h C4h C5h C6h Cnh	CC6 ±C4 CC10 ±C6 ±Cn / CC2n	[2,3+] [2,4+] [2,5+] [2,6+] [2,n+]	6 8 10 12 2n

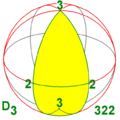
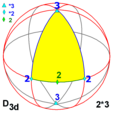
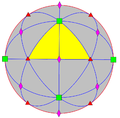
Діедрична симетрія

Див. також: Діедрична група

Існує три нескінченних сімейства з діедричною симетрією^[en] з n рівним 2 і більше (n може дорівнювати 1 як особливий випадок).

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
222	2.2	222	D2	D4	[2,2]+	4
42m	42	2*2	D2d	DD8	[2+,4]	8
mmm	22	*222	D2h	±D4	[2,2]	8

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
32 422 52 622	3.2 4.2 5.2 6.2 n.2	223 224 225 226 22n	D3 D4 D5 D6 Dn	D6 D8 D10 D12 D2n	[2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+	6 8 10 12 2n
3m 82m 5m 12.2m	62 82 10.2 12.2 n2	2*3 2*4 2*5 2*6 2*n	D3d D4d D5d D6d Dnd	±D6 DD16 ±D10 DD24 DD4n / ±D2n	[2+,6] [2+,8] [2+,10] [2+,12] [2+,2n]	12 16 20 24 4n
6m2 4/mmm 10m2 6/mmm	32 42 52 62 n2	*223 *224 *225 *226 *22n	D3h D4h D5h D6h Dnh	DD12 ±D8 DD20 ±D12 ±D2n / DD4n	[2,3] [2,4] [2,5] [2,6] [2,n]	12 16 20 24 4n

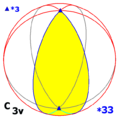
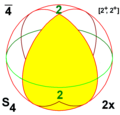
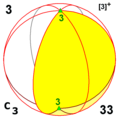
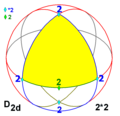
Симетрії многогранників

Існує три типи симетрії многогранників^[en]: тетраедрична симетрія, октаедрична симетрія^[en] і ікосаедрична симетрія, названі за правильними многогранниками з трикутними гранями, які мають відповідні симетрії.

Тетраедрична симетрія

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
23	3.3	332	T	T	[3,3]+ = [4,3+]+	12
m3	43	3*2	Th	±T	[4,3+]	24
43m	33	*332	Td	TO	[3,3] = [1+,4,3]	24

Октаедрична симетрія

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
432	4.3	432	O	O	[4,3]+ = [[3,3]]+	24
m3m	43	*432	Oh	±O	[4,3] = [[3,3]]	48

Ікосаедрична симетрія

Міжн.	Геом.	Орб.	Шенф.	Конвей	Кокс.	Пор.	Фунд. область
532	5.3	532	I	I	[5,3]+	60
532/m	53	*532	Ih	±I	[5,3]	120

Див. також

• Кристалографічна точкова група симетрії
• Група трикутника
• Список планарних груп симетрії^[en]
• Точкові групи у двовимірному просторі^[en]