圓周率

圆周率（一般用希腊字母π表示）是数学里向一只常数，定义是圆周同直径之比或者是圆面积搭仔半径平方之比。为著讲渠是精确计算圆周、圆面积、球体积咾啥几何量个关键值。近似等于3.14159。

直径是1个单位个圆，
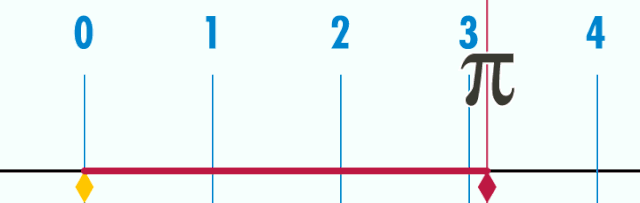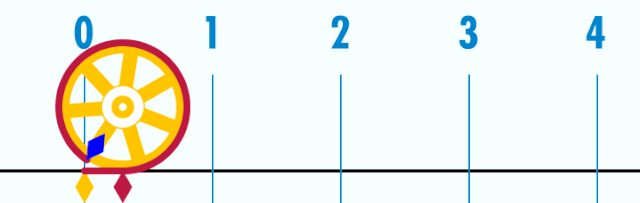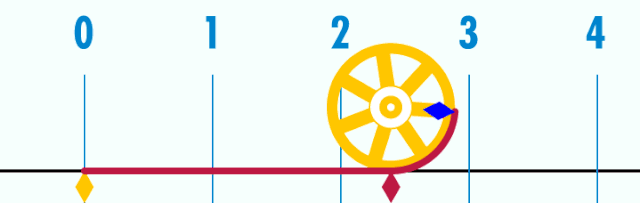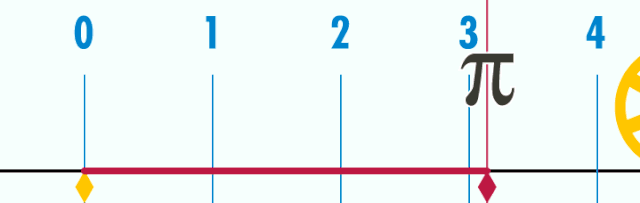
佢个周长为π个单位

圆周率是只无理数（弗好用分数准确表示），也是只超越数（弗好用有理数多项式个根表示）。来拉分析学里，渠好严格定义为满足sin(x)顶小个正实数x。

年表

年份	计算者	π值（世界纪录用粗体表示）
前20世纪	埃及人阿美斯纸草书	(16/9)² = 3.160493...
前19世纪	巴比伦人	25/8 = 3.125
前12世纪	中国人《周髀算经》	3
前9世纪	印度人《百道梵书》	339/108 = 3.138888...
前6世纪中	《圣经》列王记上7章23节	3（有人称经文内藏135/43 = 3.13953488...）
约前250年	阿基米德	223/71 <π< 22/7(3.140845... < π < 3.142857...) 211875/67441 = 3.14163491...
前20年	维特鲁威	25/8 = 3.125
前50年－23年	刘歆	3.1547
130年	张衡	92/29 = 3.17241... √10 = 3.162277... 730/232 = 3.146551...
150年	托勒密	377/120 = 3.141666...
250年	王蕃	142/45 = 3.155555...
263年	刘徽	3.141024 < π < 3.142704 3927/1250=3.1416
400年	何承天	111035/35329 = 3.142885...
480年	祖冲之	3.1415926 <π< 3.1415927 约率22/7；密率355/113（=3.1415929...）
499年	阿耶波多	62832/20000 = 3.1416
640年	婆罗摩笈多	√10 = 3.162277...
800年	花拉子密	3.1416
1150年	婆什迦罗	3.14156
1220年	斐波那契	3.141818
1320年	赵友钦	3.141592+

别样表示法

• 1579年Viete：${\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots }$
• 1650年John Wallis：${\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots }$
• 1671年Gregory Jame、1673年Leibniz：${\displaystyle \arctan z=z\frac {z^{3}}{3}}+{\frac {z^{5}}{5}{\frac {z^{7}}{7}}+\cdots }$
• 1706年Machin：${\displaystyle {\frac {\pi }{4}}=4\,\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}}$
• 18世纪欧拉：${\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }$
• 1995年贝利－波尔温－普劳夫公式：${\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}\frac {2}{8k+4}{\frac {1}{8k+5}}\frac {1}{8k+6}}\right)}$（不同于别样表示法，只公式好计算任意位数个小数，好甭先计算前头个位数。）

求算过程

古人最初估计圆周率为 3，之所谓“周三径一”。后来有人发现有理数 22/7 可以当做圆周率个近似值，叫做约率。中国南北朝数学家祖冲之发现有理数 355/113 （3.1415929203539823008849557522124）更加接近，个咾叫做密率。

日本个数学家三上义夫为仔记念伊个成就，提议将该只近似值叫做祖率。对于一般个应用里向，3.14 或约率 22/7 已经足够，但是工程学总是利用 3.1416（5位有效数字）或 3.14159（6位有效数字）。至于密率 355/113 就是一个易于记忆（“一一三三五五”）、精确至 7 位有效数字个分数，外加张景中证明佢是分母不超过16586个辰光顶准确个分数（再精确点个是52163/16604）。

微积分搭仔无穷数列出现，数学家以此作笔算。1424年，求得小数点后十六位。1596年到1610年，荷兰数学家鲁道夫·范·柯伊伦从廿位小数算到三十五位，德国人讴圆周率“鲁道夫数”。1706年，英国数学家威廉·琼斯首先用π（<希腊语περίμετρος“周长”）表示圆周率（正式推开要等欧拉用到《解析学》里）。1789年，得小数点后一百四十位；1873年，谢克斯以十五年个辰光，算得此小数点后七百五十三位。

电算机发明后，勒1949年，溤诺曼以七十小时辰光算得小数点后二千零三十七位。1985年，数学家以拉马努金算式求得小数点后千万位。1989年，求得小数点后十亿位。2002年，得小数点后一万亿位。

维基共享资源里向寻得着搭该篇文章搭界个多媒体资源：

圆周率