十一面体

在几何学中，十一面体（英语：Hendecahedron）是指具有十一个面的多面体^[1]。没有任何十一面体是正十一面体，也就是说找不到面由正多边形组成且每个面全等、每个角相等的十一面体。

十一面体

部分的十一面体 双对称十一面体 五角锥台锥 正五角锥柱 截顶角五方偏方面体 侧锥六角柱 二侧锥三角柱

命名

十一面体的英文是Hendecahedron，其命名方式为Hen-代表一，deca代表十，然后结合多面体字尾-hedron，就得到十一面体Hendecahedron^[2]。

常见的十一面体

在所有凸十一面体中，包含镜射像共有440,564种拓朴结构明显差异的凸十一面体^[3][4]。拓朴结构有明显差异意味着两种多面体无法透过移动顶点位置、扭曲或伸缩来相互变换的多面体，例如五角锥柱和九角柱无论如何变形都无法互相变换，因此拓朴结构不同，但九角柱和九角锥台可以透过伸缩其中一个九边形面来彼此互换，因此三角柱和三角锥台在拓朴上并无明显差异。

常见的十一面体有锥体和柱体、部分的约翰逊多面体和半正多面体，此处的半正多面体并非阿基米德立体，而是正九角柱。

其他十一面体还有九角柱、十角锥、正五角锥反角柱的对偶、双对称十一面体等多面体，其中双对称十一面体可以密铺空间。^[5]

三角丸塔

正三角丸塔

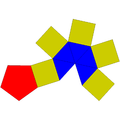
三角丸塔是指以三角形为底的丸塔，是一种十一面体，由1个三角形顶面、1个六边形底面、3个五边形侧面和6个三角形侧面组成，共有11个面、21条边和12个顶点，其中顶面的三角形与底面的六边形互相平行，侧面的三角形与五边形交错地围绕轴分布在周围。

以正三角形为底的三角丸塔称为正三角丸塔，其仅有顶面和底面为正多边形，分别为顶面的正三边形和底面的正六边形，侧面可能可以存在正三角形或存在正五边形，但有正三角形面时，五边形最多仅能是等边不等角的非正五边形；有正五边形面时，三角形会出现等腰三角形，故不属于约翰逊多面体。唯一属于约翰逊多面体的丸塔仅有正五角丸塔^[6]。

正三角丸塔的对称群为C_3v（英语：Dihedral symmetry in three dimensions）群，阶数为6阶。

截半三角柱

截半三角柱的旋转动画

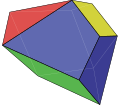
在几何学中，截半三角柱是指经过截半变换后的三角柱，是一种十一面体^[7]，其侧面是正方形、底面是正三角形，另外还有6个等腰三角形面。

截半三角柱可由三角柱将边的中点当作新的顶点，旧的顶点消失，来构造，换句话说，即是用三角柱由一条棱斩到另一条棱的中点（即斩去三角柱的顶点，但不是截角）而成。

其具有D_3h二面体群的对称性。

约翰逊多面体

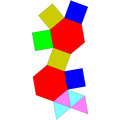
在十一面体中，有3个是约翰逊多面体，它们分别为:正五角锥柱、二侧锥三角柱、侧锥六角柱。

名称	种类	图像	编号	顶点	边	面	面的种类	对称性	展开图
正五角锥柱	角锥柱		J9[8]	11	20	11	5个正三角形 5个正方形 1个正五边形	C5v, [5], (*55)
二侧锥三角柱	锥体与柱体的组合		J50[9]	8	17	11	10个正三角形 1个正方形	C2v
侧锥六角柱	锥体与柱体的组合		J54[10]	8	17	11	4个正三角形 5个正方形 2个六边形	C2v

九角柱

正九角柱

主条目：九角柱

九角柱是一种底面为九边形的柱体，是十一面体的一种，由11个面、27条边和18个顶点组成^[11]，对偶多面体为双九角锥^[12]。正九角柱代表每个面都是正多边形的九角柱，其每个顶点都是2个正方形和1个九边形的公共顶点，因此具有每个角等角的性质，可以归类为半正十一面体。而顶点都是2个正方形和1个九边形的公共顶点的这种顶角，在顶点图中以${\displaystyle 4{.}4{.}9}$表示。正九角柱在施莱夫利符号中可以利用{9}×{} 或 t{2, 9}来表示；在考克斯特—迪肯符号（英语：Coxeter-Dynkin diagram）中可以利用来表示；在威佐夫符号（英语：Wythoff symbol）中可以利用2 9 | 2来表示；在康威多面体表示法中可以利用P9来表示。若一个正九角柱底边的边长为${\displaystyle s}$、高为${\displaystyle h}$，则其体积${\displaystyle V}$和表面积${\displaystyle S}$为^[13]：

${\displaystyle V={\frac {9hs^{2}\cot {\frac {\pi }{9}}}{4}}\approx 6.18182hs^{2}}$

${\displaystyle S=9s\left(h+{\frac {1}{2}}s\cot {\frac {\pi }{9}}\right)\approx 9s\left(h+1.37374s\right)}$

十角锥

十角锥是一种底面为十边形的锥体，是十一面体的一种，由11个面、20条边和11个顶点组成^[14]，其对偶多面体是自己本身^[15]。正十角锥是一种底面为正十边形的十角锥。若一个正十角锥底边的边长为${\displaystyle s}$、高为${\displaystyle h}$，则其体积${\displaystyle V}$和表面积${\displaystyle S}$为^[15]：

${\displaystyle V={\frac {5{\sqrt {5+2{\sqrt {5}}}}}{6}}hs^{2}\approx 2.56474hs^{2}}$

${\displaystyle S={\frac {5s\left({\sqrt {4h^{2}+\left(5+2{\sqrt {5}}\right)s^{2}}}+{\sqrt {5+2{\sqrt {5}}}}s\right)}{2}}\approx 2.5s\left({\sqrt {4h^{2}+9.47214s^{2}}}+3.07768s\right)}$

十一面体列表

名称	种类	图像	符号	顶点	边	面	χ	面的种类	对称性	展开图
九角柱	棱柱体		t{2,9} {9}x{}	18	27	11	2	2个九边形 9个矩形	D9h, [9,2], (*922), order 36
十角锥	棱锥体		( )∨{10}	11	20	11	2	1个十边形 10个三角形	C10v, [10], (*10 10)
五角锥柱	角锥柱 约翰逊多面体		P5+Y5	11	20	11	2	5个三角形 5个正方形 1个五边形	C5v, [5], (*55)
五角锥台锥	截角双锥			11	20	11	2	1个五边形 5个梯形 5个三角形	C5v, [5], (*55)
三角丸塔	丸塔			12	21	11	2	1个三角形顶面 1个六边形底面 3个五边形侧面 6个三角形侧面	C3v（英语：Dihedral symmetry in three dimensions）, [3], (*33), order 6
截顶角五方偏方面体	截顶角偏方面体			16	25	11	2	1个五边形底面 5个五边形侧面 5个筝形侧面	C5v, [5], (*55)
截半三角柱				9	18	11	2	2个三角形 3个正方形 6个等腰三角形	D3h, [3,2], (*322), order 12
截半双三角锥				9	18	11	2	3个正方形 8个三角形	D3h, [3,2], (*223) order 12
双对称十一面体	空间充填多面体			11	20	11	2	4个筝形 2个菱形 4个等腰三角形 1个正方形

在化学中

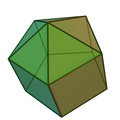
在化学中，将十八面体硼烷离子([B₁₁H₁₁]²⁻)的氢全部去掉后，可以得到一个结构，它是十八面体，再将每个硼原子做垂直于重心到硼原子的面，可构造成新的多面体，即为十八面体硼烷结构的对偶多面体，也是十一面体之一。^[16]

双对称十一面体

双对称十一面体（Bisymmetric Hendecahedron）是十一面体的一种多面体

帕雷托和阿基米德立体，只有少数可以密铺于空间，也就是说堆砌在一起，不留空隙，以填补空间。Guy Inchbald描述了一个有趣的多面体，可以以令人惊讶的方式利用11面体完成空间的密铺。^[5][17][18]

图像	旋转动画	展开图

曾有人提出一个十一面体^[5]，它的面数和顶点数是相同的^[19]，经过扭曲后，会得到不同的特性。最对称的自身对偶十一面体是双对称十一面体^[20]，它之所以会称为双对称是因为它有两个对称面^[19]。