广底加长型球状屋顶

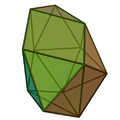
广底加长型球状屋顶（日语：広底長球形屋根、英语：Hebesphenomegacorona）是一种由18个三角形和3个正方形组成的二十一面体^[1]，为约翰逊多面体的其中一个，索引为J₈₉^[2]。它无法由帕雷托立体（正多面体）和阿基米得立体（半正多面体）经过切割、增补而得来，是约翰逊多面体中的基本立体之一。约翰逊多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·约翰逊（英语：Norman Johnson (mathematician)）（Norman Johnson）命名并给予描述^[3]。

广底加长型球状屋顶

类别	约翰逊多面体 J88 - J89 - J90
识别
名称	广底加长型球状屋顶 Hebesphenomegacorona
别名	広底長球形屋根（日语）
参考索引	J89
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	hawmco
性质
面	21
边	33
顶点	14
欧拉特征数	F=21, E=33, V=14 （χ=2）
组成与布局
面的种类	3×2+3×4个三角形 1+2个正方形
顶点图	4个(32.42) 2+2×2个(35) 4个(34.4)
对称性
对称群	C2v群
特性
凸
图像
（展开图）

性质

广底加长型球状屋顶共由21个面、33条边和14个顶点所组成^[4][5][6][7]。在其21个面中，有18个三角形和3个正方形^[5][7]。在其14个顶点中，6个顶点是5个三角形的公共顶点^[7]，在顶点图中可以用[3⁵]来表示^[8]、还有4个顶点是4个三角形和1个正方形的公共顶点^[7]，在顶点图中可以用[3⁴,4]来表示^[8]、剩下的4个顶点是2个三角形和2个正方形的公共顶点^[7]，在顶点图中可以用[3²,4²]来表示^[8]。

体积与表面积

若一个广底加长型球状屋顶边长为${\displaystyle a}$，则其表面积${\displaystyle A}$为：^[9]

${\displaystyle A=3+{\frac {9{\sqrt {3}}}{2}}a^{2}\approx 10.7942a^{2}}$^[10]

在92种约翰逊多面体中，有13种约翰逊多面体的单位边长体积（V/a³）无法表达为解析数。而五角锥球状屋顶就是这13种约翰逊多面体之一。

由于其体积无法表达为解析数，但可以用近似值表示。边长为${\displaystyle a}$的五角锥球状屋顶体积近似为：

${\displaystyle V\approx 2.9129104145402091660a^{3}}$^[5]。

上述体积近似值为以下多项式的最大实根：^[11]

47330370277129322496 x20 − 722445512980071186432 x18 + 3596480447590271287296 x16 − 8432333285523990773760 x14 + 8973584611317745975296 x12 − 3065290664181478981632 x10 + 366229890219212144640 x8 − 8337259437908852736 x6 − 22211277300912896 x4 + 132615435213216 x2 + 2693461945329

顶点坐标

令${\displaystyle a}$ ≈ 0.216844815713457为下列多项式的第二小实根：^[6]

${\displaystyle {\begin{aligned}&26880x^{10}+35328x^{9}-25600x^{8}-39680x^{7}+6112x^{6}\\&\quad {}+13696x^{5}+2128x^{4}-1808x^{3}-1119x^{2}+494x-47\end{aligned}}}$

则边长为2的广底加长型球状屋顶的顶点坐标为：^[6]

${\displaystyle \left(\pm 1,\,\pm 1,\,2b\right)}$

${\displaystyle \left(\pm 1,\,\pm \left(1+2a\right),\,0\right)}$

${\displaystyle \left(\pm \left(1+{\frac {c}{\sqrt {1-a}}}\right),\,0,\,-{\frac {2a^{2}+a-1}{b}}\right)}$

${\displaystyle \left(0,\,\pm 1,\,-d\right)}$

${\displaystyle \left(\pm {\frac {dc+e}{fe}},\,0,\,{\frac {\left(2a-1\right)d}{f}}-{\frac {c}{fe}}\right)}$

其中，${\displaystyle b}$、${\displaystyle c}$、${\displaystyle d}$、${\displaystyle e}$和${\displaystyle f}$分别为：^[6]

${\displaystyle b={\sqrt {1-a^{2}}}}$

${\displaystyle c={\sqrt {2\left(1-2a\right)}}}$

${\displaystyle d={\sqrt {3-4a^{2}}}}$

${\displaystyle e={\sqrt {1+a}}}$

${\displaystyle f=2\left(1-a\right)}$

这些坐标也可以由下列顶点的轨道的并集在沿xz平面和yz平面镜射所产生的空间对称群之群作用下给出：^[12]

${\displaystyle {\begin{aligned}&\left(1,1,2{\sqrt {1-a^{2}}}\right),\ \left(1+2a,1,0\right),\ \left(0,1+{\sqrt {2}}{\sqrt {\frac {2a-1}{a-1}}},-{\frac {2a^{2}+a-1}{\sqrt {1-a^{2}}}}\right),\ \left(1,0,-{\sqrt {3-4a^{2}}}\right),\\&\left(0,{\frac {{\sqrt {2(3-4a^{2})(1-2a)}}+{\sqrt {1+a}}}{2(1-a){\sqrt {1+a}}}},{\frac {(2a-1){\sqrt {3-4a^{2}}}}{2(1-a)}}-{\frac {\sqrt {2(1-2a)}}{2(1-a){\sqrt {1+a}}}}\right)\end{aligned}}}$

相关多面体

广底加长型球状屋顶欠侧锥

广底加长型球状屋顶欠侧锥（Diminished hebesphenomegacorona）是指从广底加长型球状屋顶上移除一个五角锥所构成的立体，然而，直接将五角锥从广底加长型球状屋顶移除将会出现一个不共面五边形，无法构成多面体，需要将顶点位置些微调整，才能将五边形面放置到移除五角锥的位置，这将导致广底加长型球状屋顶欠侧锥的面仅是很接近正多边形而不是正多边形，因此是一种拟约翰逊多面体。

• 
  广底加长型球状屋顶
• 
  广底加长型球状屋顶欠侧锥
• 
  广底加长型球状屋顶欠侧锥的3D模型

其他立体

• 
  球状屋顶
  （原始的球状屋顶立体）
• 
  球状屋顶欠侧锥
  （移除一个五角锥的球状屋顶）
• 
  侧锥球状屋顶
  （在正方形面叠上正四角锥的球状屋顶）
• 
  加长型球状屋顶
  （正方形附近的4个位置上各加上1个正三角形的球状屋顶）
• 
  广底加长型球状屋顶
  （“屋顶”部分由3个正方形组成的球状屋顶）
• 
  广底加长型球状屋顶欠侧锥
  （移除一个五角锥的广底加长型球状屋顶）
• 
  五角锥球状屋顶
  （合并两个移除了两个正三角形的球状屋顶）

参见

• 约翰逊多面体
• 多面体