截角十二面体

在几何学中，截角十二面体是一种由正十边形和正三角形组成的三十二面体^[1]，是一种阿基米德立体^[2]。其每个顶点都是1个三角形和2个十边形的公共顶点，具有每个顶角相等的性质，因此截角十二面体是一种半正多面体^[3]。

截角十二面体

(按这里观看旋转模型)
类别	半正多面体
对偶多面体	三角化二十面体
识别
名称	截角十二面体
参考索引	U26, C29, W10
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	tid
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	t{5,3}
威佐夫符号 （英语：Wythoff symbol）	2 3 | 5
康威表示法	tD
性质
面	32
边	90
顶点	60
欧拉特征数	F=32, E=90, V=60 （χ=2）
组成与布局
面的种类	正三角形 正十边形
面的布局 （英语：Face configuration）	20个{3} 12个{10}
顶点图	3.10.10
对称性
对称群	Ih群
特性
-
图像
3.10.10 （顶点图） 三角化二十面体 （对偶多面体） （展开图）

性质

截角十二面体共有32个面、90条边和60个顶点^[4]，每个顶点都是1个三角形和2个十边形的公共顶点，其顶点图可以用3.10.10来表示，也可以简写为3.10^2[5]。

构造

截角十二面体可以经由正十二面体透过截角变换构造而成。截角变换使得正十二面体原本的正五边形面变成正十边形面，并在原本的顶点处形成正三角形。

体积与表面积

边长为a的截角十二面体体积V和表面积A分别为：

${\displaystyle A=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\approx 100.990\,76a^{2}}$

${\displaystyle V={\frac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}\approx 85.039\,6646a^{3}}$

顶点坐标

边长为2φ − 2且几何中心位于原点的截角十二面体^[6]其顶点坐标为^[7]：

${\displaystyle \left(0\,,\pm {\frac {1}{\varphi }}\,,\pm {\left({\begin{smallmatrix}2+\varphi \end{smallmatrix}}\right)}\right)}$、

${\displaystyle \left(\pm {\frac {1}{\varphi }}\,,\pm {\varphi }\,,\pm {2{\varphi }}\right)}$、

(±φ, ±2, ±(φ + 1))。

其中φ = ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$，为黄金比例.

球面镶嵌和施莱格尔图

截角十二面体对应的结构也可以构建成球面镶嵌，并以球极平面投影的方式呈现。

正投影图（英语：Orthographic projection）	球极平面投影
	以十边形为中心	以正三角形为中心
透视图	施莱格尔图

顶点布局

有一些多面体与截角十二面体具有相同的顶点布局（英语：Vertex_arrangement），换句话说，及他们与截角十二面体共用顶点、或者可以具有相同的顶点坐标。这些多面体有^[8][9][10]：

截角十二面体（原像）

大二十合二十合十二体（英语：Great icosicosidodecahedron）

大双三角十二面截半二十面体

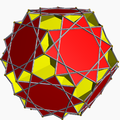大十二合二十面体（英语：Great dodecicosahedron）

相关多面体及密铺

截角二十面体是正二十面体经过截半变换后的结果，其他也是由正二十面体透过康威变换得到的多面体有：

正二十面体家族半正多面体

对称群: [5,3]（英语：Icosahedral symmetry）, (*532)							[5,3]+, (532)
{5,3}	t0,1{5,3}	t1{5,3}	t0,1{3,5}	{3,5}	t0,2{5,3}	t0,1,2{5,3}	s{5,3}
半正多面体对偶
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

截角二十面体可以独立填满双曲仿紧三维空间，这种由几何结构称为截角十二面体堆砌^[11]。

参见

• 正十二面体