三角柱可以由三角形二面体的对偶三面形透过截角变换构造而来,因此与三角形二面体具有相同的对称性,其可以衍生出一些相关的多面体:
更多信息 [3,2]+, (322), 半正对偶 ...
半正三角形二面体球面多面体
| 对称群:[3,2], (*322)
|
[3,2]+, (322)
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|
|

|

|
{3,2}
|
t{3,2}
|
r{3,2}
|
2t{3,2}=t{2,3}
|
2r{3,2}={2,3}
|
rr{3,2}
|
tr{3,2}
|
sr{3,2}
|
| 半正对偶
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|

|

|

|
| V32
|
V62
|
V32
|
V4.4.3
|
V23
|
V4.4.3
|
V4.4.6
|
V3.3.3.3
|
关闭
更多信息 球面镶嵌, 柱体 ...
柱体形式半正镶嵌系列:
| 球面镶嵌
|
柱体
|
欧式镶嵌
仿紧空间
|
双曲镶嵌
非紧空间
|

t{2,1}
  
|

t{2,2}
    
|

t{3,2}
    
|

{4,2}
    
|

t{5,2}
    
|

t{6,2}
    
|

t{7,2}
    
|

t{8,2}
    
|
...
|

t{2,∞}
    
|

t{2,iπ/λ}
    
|
关闭
更多信息 对称性*n32 [n,3], 球面 ...
截角多面体和镶嵌系列:3.2n.2n
对称性 *n32
[n,3]
|
球面
|
欧氏镶嵌
|
紧凑型双曲镶嵌
|
仿紧型镶嵌
|
非紧型镶嵌
|
*232
[2,3]
D3h
|
*332
[3,3]
Td
|
*432
[4,3]
Oh
|
*532
[5,3]
Ih
|
*632
[6,3]
P6m
|
*732
[7,3]
|
*832
[8,3]...
|
*∞32
[∞,3]
|
[iπ/λ,3]
|
| 截角顶点布局
|

3.4.4
|

3.6.6
|

3.8.8
|

3.10.10
|

3.12.12
|

3.14.14
|

3.16.16
|

3.∞.∞
|

3.∞.∞
|
考克斯特纪号
施莱夫利符号
|
    
t{2,3}
|
    
t{3,3}
|
    
t{4,3}
|
    
t{5,3}
|
    
t{6,3}
|
    
t{7,3}
|
    
t{8,3}
|
    
t{∞,3}
|
    
t{∞,3}
|
| 半正对偶图
|
三角化
顶点布局
|

V3.4.4
|

V3.6.6
|

V3.8.8
|

V3.10.10
|

V3.12.12
|

V3.14.14
|

V3.16.16
|

V3.∞.∞
|
V3.∞.∞
|
| 考克斯特纪号
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
关闭
更多信息 对称群*n32 [n,3], 球面镶嵌 ...
半正小斜方截半家族:3.4.n.4
对称群
*n32
[n,3]
|
球面镶嵌
|
欧氏镶嵌
|
紧凑型双曲镶嵌
|
仿紧型镶嵌
|
非紧型镶嵌
|
*232
[2,3]
D3h
|
*332
[3,3]
Td
|
*432
[4,3]
Oh
|
*532
[5,3]
Ih
|
*632
[6,3]
P6m
|
*732
[7,3]
|
*832
[8,3]...
|
*∞32
[∞,3]
|
[iπ/λ,3]
|
小斜方截半
顶点布局
|

3.4.2.4
|

3.4.3.4
|

3.4.4.4
|

3.4.5.4
|

3.4.6.4
|

3.4.7.4
|

3.4.8.4
|

3.4.∞.4
|

3.4.∞.4
|
考克斯特符号
施莱夫利符号
|
    
rr{2,3}
|
    
rr{3,3}
|
    
rr{4,3}
|
    
rr{5,3}
|
    
rr{6,3}
|
    
rr{7,3}
|
    
rr{8,3}
|
    
rr{∞,3}
|
    
rr{iπ/λ,3}
|
筝形
顶点布局
|

V3.4.2.4
|

V3.4.3.4
|

V3.4.4.4
|

V3.4.5.4
|

V3.4.6.4
|
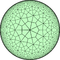
V3.4.7.4
|

V3.4.8.4
|

V3.4.∞.4
|
V3.4.∞.4
|
| 考克斯特符号
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
关闭



















































