虫洞

虫洞（英语：Wormhole），又称爱因斯坦-罗森桥（英语：Einstein—Rosen bridge），是一种连接时空中不同点的理论结构，它基于爱因斯坦场方程的特殊解。它们于1916年由路德维希·弗拉姆（英语：Ludwig Flamm）首次提出，并于1935年由阿尔伯特·爱因斯坦和内森·罗森再次提出。因此，它们也被称为爱因斯坦-罗森桥。^[2] 虫洞一词是由约翰·阿奇博尔德·惠勒在1957年创造的，^[3] 而虫洞这个名字有“虫咬的洞”的意思，其举例来自如果一只虫要苹果表面移动，比起沿着表面爬，不如直接从果肉穿过距离更短。^[4]

若地面附近有一个虫洞，它可能是这样的^[1]

虫洞可以想像成一条隧道，其两端位于时空的不同点（可能是不同的位置和时间）。

虫洞与广义相对论是相容的，但虫洞是否真的存在还有待观察。许多科学家假设虫洞只是第四空间维度的投影，类似于二维生物如何只能体验三维物体的一部分^[5] 克莱因瓶提供了这种结构的一个众所周知的类比，在三维渲染时显示一个孔，而不是在四维或更高维度上。

理论上，一个虫洞可能连接十亿光年这样的极远距离，也可能连接几米这样的短距离，或者不同的时间点，甚至不同的宇宙。^[6]

1995年，马特·维瑟（英语：Matt Visser）提出，如果在早期宇宙中生成负质量/负能量的宇宙弦，宇宙中可能存在许多虫洞。^[7][8] 一些物理学家，例如弗兰克·迪普勒和基普·索恩，提出了如何人工制造虫洞。^{[来源请求]}

可视化

被视觉化为2D的虫洞

对于虫洞的简化概念，空间可以被想象为二维表面。虫洞会出现在该表面上的一个洞，通向一个三维管道（圆柱体的内表面），然后重新出现在二维表面上的另一个位置，并有一个与入口类似的洞。实际的虫洞与此类似，但空间维度增加了一维。例如，入口和出口点可以被视为三维空间中的球形孔，而不是二维平面上的圆形孔，通向类似于球体的四维“管道”。 ^{[需要引用]}

另一种虫洞在二维环境的模拟

想象虫洞的另一种方式是拿一张纸并在纸的一侧画两个稍远的点。这张纸代表时空连续体中的一个平面，而这两个点代表要行进的距离，但理论上，虫洞可以通过折叠该平面（即纸张）使这两个点接触来连接这两个点。这样，由于两点现在相切，穿越距离就会变得容易得多。 ^{[需要引用]}

发展过程

史瓦西虫洞的“嵌入图”

史瓦西虫洞

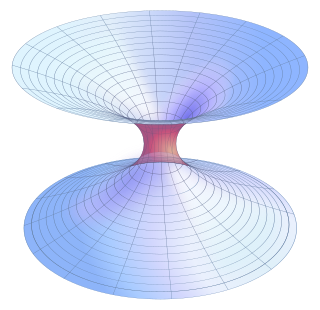
发现的第一种虫洞解决方案是史瓦西虫洞，它存在于描述永恒黑洞的史瓦西度规中，但人们发现它坍缩得太快，任何东西都无法从一端穿过到另一端。人们认为，只有使用具有负能量密度的奇异物质来稳定虫洞，才有可能形成可以双向穿越的虫洞，又称为可穿越虫洞。 ^[9]后来，物理学家报告称，微观可穿越虫洞可能是可能的，而且不需要任何奇异物质，而只需要带电费米子物质，其质量足够小，不会坍缩成带电黑洞。 ^{[10] [11] [12]}尽管这种虫洞（如果可能的话）可能仅限于信息传输，但如果现实可以用兰德尔-桑德拉姆模型 2 （一种与弦理论一致的基于膜的理论）广泛描述，那么人类可穿越的虫洞可能存在。 ^[13]

爱因斯坦–罗森桥

爱因斯坦-罗森桥(或ER 桥) 以阿尔伯特·爱因斯坦和内森·罗森的名字命名， 是空间区域之间的连接，可以建模为爱因斯坦场方程的真空解，现在被理解为史瓦西度量的最大扩展版本的内在部分，描述一个没有电荷和旋转的永恒黑洞。这里，“最大程度延伸”指的是时空不应该有任何“边缘”：对于自由落体粒子的任何可能轨迹（沿着时空中的测地线），这条路径应该可以任意延伸到粒子的未来或过去。

为了满足这一要求，事实证明，除了粒子从外部穿过事件视界时进入的黑洞内部区域之外，还必须有一个单独的白洞内部区域，以便我们推断外部观察者看到的粒子从事件视界上升起的轨迹。 ^[14]正如最大延伸时空有两个独立的内部区域一样，也存在两个独立的外部区域，有时被称为两个不同的“宇宙”，第二个宇宙使我们能够推断两个内部区域中一些可能的粒子轨迹。这意味着黑洞内部区域可以包含来自任一宇宙的混合粒子（因此从一个宇宙落入的观察者可能能够看到从另一个宇宙落入的光），同样，来自白洞内部区域的粒子可以逃逸到任一宇宙。所有四个区域都可以在使用克鲁斯卡尔-塞凯列斯坐标的时空图中看到。

在这个时空中，可以提出这样的坐标系：如果选择一个常数时间的超曲面（一组具有相同时间坐标的点，使得曲面上的每个点都有一个类空间分离，从而产生所谓的“类空间曲面”）并绘制一个描绘当时空间曲率的“嵌入图”，则嵌入图将看起来就像连接两个外部区域的管道，称为“爱因斯坦-罗森桥”。史瓦西度规描述的是从外部观察者的角度永远存在的理想黑洞；而由坍缩恒星在特定时间形成的更现实的黑洞则需要不同的度规。当坠落的恒星物质被添加到黑洞地理图上时，它会移除对应于白洞内部区域的部分图表，以及对应于另一个宇宙的部分图表。

爱因斯坦-罗森桥由路德维希·弗拉姆于 1916 年发现， ^[15]就在史瓦西发表他的解法几个月后。后来，阿尔伯特·爱因斯坦和他的同事内森·罗森重新发现了爱因斯坦-罗森桥，并于 1935 年发表了他们的成果。 ^[16] 1962 年，约翰·阿奇博尔德·惠勒 (John Archibald Wheeler)和罗伯特·W·富勒 (Robert W. Fuller)发表了一篇论文^[17] ，指出这种类型的虫洞如果连接同一宇宙的两个部分，则是不稳定的，并且它会很快切断，使得从一个外部区域落入的光（或任何速度比光慢的粒子）无法到达另一个外部区域。

根据广义相对论，足够致密的质量的引力坍缩会形成一个奇异的史瓦西黑洞。然而，在爱因斯坦-嘉当-夏马-基布尔引力理论中，它形成了一个规则的爱因斯坦-罗森桥。该理论通过消除仿射联络对称性的约束并将其反对称部分扭转张量视为动态变量，扩展了广义相对论。扭转自然地解释了物质的量子力学、内在角动量（自旋）。扭转和狄拉克旋量之间的最小耦合会产生排斥性的自旋-自旋相互作用，这在极高密度的费米子物质中非常重要。这种相互作用阻止了引力奇点（例如黑洞）的形成。相反，坍缩的物质会达到巨大但有限的密度并反弹，形成桥的另一侧。 ^[18]

尽管史瓦西虫洞无法双向穿越，但它的存在启发了基普·索恩想象通过用奇异物质（具有负质量/能量的物质）将史瓦西虫洞的“喉咙”打开，从而形成可穿越的虫洞。 ^[19]

其他不可穿越的虫洞包括洛伦兹虫洞（由约翰·阿奇博尔德·惠勒于 1957 年首次提出）、在用洛伦兹流形描绘的广义相对论时空流形中创建时空泡沫的虫洞^[20] ，以及欧几里得虫洞（以欧几里得流形命名，欧几里得流形是黎曼流形的一种结构）。

可穿越的虫洞

卡西米尔效应表明，量子场论允许空间某些区域的能量密度相对于普通物质的真空能量为负，并且理论上已经证明，量子场论允许能量在给定点任意为负的状态。 ^[21]许多物理学家，如史蒂芬·霍金、 ^[22]基普·索恩、 ^[23]等人， ^{[24] [25] [26]}认为，这种效应可能使可穿越虫洞成为稳定。 ^[27]在广义相对论和量子力学的背景下，唯一已知的、理论上预测会形成虫洞的自然过程是由胡安·马尔达西那和伦纳德·萨斯坎德在他们的ER = EPR猜想中提出的。量子泡沫假说有时被用来表明微小虫洞可能在普朗克尺度上自发出现和消失， ^{[28] :494–496[29]}此类虫洞的稳定版本已被提议作为暗物质的候选者。 ^{[30] [31]}还有人提出，如果在大爆炸前后出现了一个由负质量宇宙弦保持开放的微小虫洞，那么它可能会在宇宙膨胀的作用下膨胀到宏观尺寸。 ^[32]

模拟可穿越虫洞的图像，连接图宾根大学物理研究所前的广场和法国北部滨海布洛涅附近的沙丘。该图像是使用 Morris-Thorne 虫洞度量中的 4D光线追踪计算得出的，但尚未模拟引力对光波长的影响。 ^{[注 1]}

洛伦兹可穿越虫洞可以让人非常快速地从宇宙的一部分旅行到同一宇宙的另一部分，或者从一个宇宙旅行到另一个宇宙。广义相对论中可穿越虫洞的可能性最早由 Homer Ellis 在 1973 年的一篇论文中证明^[33] ，随后 K.A. Bronnikov 在同年发表的一篇论文中独立证明了这^[34] 。埃利斯分析了埃利斯排水孔的拓扑结构和测地线，表明它是测地线完整的、无水平面的、无奇点的，并且在两个方向上完全可穿越。排水孔是爱因斯坦真空时空场方程的解流形，通过包含与具有反正统极性（负而不是正）的里奇张量最小耦合的标量场进行了修改。 （埃利斯特别拒绝将标量场称为“奇异的”，因为它具有反正统的耦合性，他认为这样做的论据缺乏说服力。）该解决方案取决于两个参数： m ，它决定了其引力场的强度，以及n ，它决定了其空间横截面的曲率。当m设置为等于 0 时，排水孔的重力场消失。剩下的就是埃利斯虫洞，一种非引力、纯几何、可穿越的虫洞。

1988 年，基普·索恩和他的研究生迈克·莫里斯分别发现了埃利斯虫洞，并主张将其作为教授广义相对论的工具。 ^[35]因此，他们提出的这种由奇异物质球壳支撑的可穿越虫洞也被称为莫里斯-索恩虫洞。

后来，其他类型的可穿越虫洞被发现是广义相对论方程的可解，其中包括马特·维瑟 (Matt Visser) 在 1989 年的一篇论文中分析的一种，其中可以制作一条穿过虫洞的路径，而穿越路径不会经过奇异物质区域。然而，在纯高斯-博内引力（广义相对论的一种修正，涉及额外空间维度，有时会在膜宇宙学的背景下进行研究）中，虫洞的存在并不需要奇异物质 —— 甚至在没有物质的情况下它们也可以存在。 ^[36]维瑟与克雷默等人合作提出了一种由负质量宇宙弦保持开放的类型， ^[32]他们认为这种虫洞可以在早期宇宙中自然形成。

虫洞连接时空中的两点，这意味着原则上它们可以实现时间旅行，也可以实现空间旅行。 1988年，莫里斯（Morris）、索恩（Thorne）和尤尔特塞弗（Yurtsever）研究出如何通过加速虫洞的两个入口之一，将穿越空间的虫洞转换为穿越时间的虫洞。 ^[23]然而，根据广义相对论，不可能利用虫洞回到早于虫洞首次被转换成时间“机器”的时间。在此之前，它不可能被注意到或被利用。 ^{[28] :504}

宇宙间的旅行

解决虫洞时间旅行悖论的一个可能方法依赖于量子力学的多重世界诠释。

1991 年，大卫·多伊奇（David Deutsch）证明，量子理论在具有封闭类时曲线的时空中是完全一致的（即所谓的密度矩阵可以不受不连续性的影响）。 ^[37]后来，人们发现，这种封闭类时曲线模型可能存在内部不一致性，因为它会导致一些奇怪的现象，比如区分非正交量子态，区分适当混合和非适当混合。 ^{[38] [39]}因此，半经典计算表明的虚拟粒子在虫洞时间机器中循环的破坏性正反馈回路被避免了。从未来返回的粒子不会返回其起源的宇宙，而是返回平行宇宙。这表明，具有极短时间跳跃的虫洞时间机器是同时存在的平行宇宙之间的理论桥梁。 ^[9]

因为虫洞时间机器在量子理论中引入了一种非线性，所以这种平行宇宙之间的通信与约瑟夫·波尔钦斯基在史蒂文·温伯格的非线性量子力学表述中提出的埃弗雷特电话^[40] （以休·埃弗雷特的名字命名）的提议一致。

平行宇宙之间进行通讯的可能性被称为宇宙间旅行。

虫洞也可以用史瓦西黑洞的彭罗斯图来描绘。在彭罗斯图中，一个运动速度超光速的物体将穿过黑洞，从另一端进入不同的空间、时间或宇宙。这将是一个宇宙间的虫洞。

度规

“虫洞度规”描述了虫洞的时空几何，并作为时间旅行的理论模型。一个（可穿越的）虫洞度规的例子如下：^[41]

${\displaystyle ds^{2}=-c^{2}\,dt^{2}+d\ell ^{2}+(k^{2}+\ell ^{2})(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}),}$

由埃利斯首次提出，此为埃利斯排水孔（英语：Ellis drainhole）的特例

一种不可穿越的虫洞的度规是史瓦西解（见第一张图）：

${\displaystyle ds^{2}=-c^{2}\left(1-{\frac {2GM}{rc^{2}}}\right)\,dt^{2}+{\frac {dr^{2}}{1-{\frac {2GM}{rc^{2}}}}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}).}$

1935年7月发表的一篇文章描述了最初的爱因斯坦-罗森桥。^[42][43]

对于史瓦西球对称静态解：

${\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}\right)\,dt^{2},}$

在这里${\displaystyle ds}$是固有时而光速${\displaystyle c=1}$

利用${\displaystyle u^{2}=r-2m}$，把${\displaystyle r}$换成${\displaystyle u}$

${\displaystyle ds^{2}=-4(u^{2}+2m)\,du^{2}-(u^{2}+2m)^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+{\frac {u^{2}}{u^{2}+2m}}\,dt^{2}}$

数学上将这个解的四维时空想成两个全等部分，或是两片纸片，根据 ${\displaystyle u>0}$ 或 ${\displaystyle u<0}$决定这个点在哪片时空部分上。这两个时空部分被${\displaystyle r=2m}$ （即 ${\displaystyle u=0}$）这个超曲面连接。我们称这样的连接是个“桥”

——爱因斯坦、罗森：“广义相对论中的粒子问题”

考虑到重力场以及电场，爱因斯坦和罗森推导出以下史瓦西静态球对称解

${\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0,\varphi _{4}={\frac {\varepsilon }{4}},}$

${\displaystyle ds^{2}=-{\frac {1}{\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)\,dt^{2},}$

${\displaystyle \varepsilon }$ 代表电荷

没有分母的场方程（在${\displaystyle m=0}$的情况下）可写为

${\displaystyle \varphi _{\mu \nu }=\varphi _{\mu ,\nu }-\varphi _{\nu ,\mu }}$

${\displaystyle g^{2}\varphi _{\mu \nu ;\sigma }g^{\nu \sigma }=0}$

${\displaystyle g^{2}(R_{ik}+\varphi _{i\alpha }\varphi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\varphi _{\alpha \beta }\varphi ^{\alpha \beta })=0}$

为了去除奇点，若把${\displaystyle r}$换为${\displaystyle u}$根据：

${\displaystyle u^{2}=r^{2}-{\frac {\varepsilon ^{2}}{2}}}$

又${\displaystyle m=0}$，可得^[44][45]

${\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0}$ and ${\displaystyle \varphi _{4}={\frac {\varepsilon }{\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)^{1/2}}}}$

${\displaystyle ds^{2}=-du^{2}-\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left({\frac {2u^{2}}{2u^{2}+\varepsilon ^{2}}}\right)\,dt^{2}}$

在这个解中，对于两张纸空间中的所有有限点，解都没有奇点

——爱因斯坦，罗森：“广义相对论中的粒子问题”

流行文化

• 虫洞是科幻小说中的常见元素，因为它们允许星际、星系间，有时甚至是人类生命尺度内的宇宙间旅行。在小说中，虫洞也被用作时间旅行的一种方法。

• 2014年科幻电影《星际效应》

参考资料