Fold (高阶函数)

在函数式编程中，折叠（fold），也称为归约（reduce）、积累（accumulate）、聚集（aggregate）、压缩（compress）或注入（inject），指称一组高阶函数，它们分析递归数据结构并通过使用给定组合运算，将递归的处理它的构成部件、建造一个返回值的结果重组起来。典型的，要向折叠提供一个组合函数，一个数据结构的顶端节点（英语：Node (computer science)），和可能的在特定条件下使用的某些缺省值。折叠接着以系统性方式使用这个函数，进行组合这个数据结构的层级中的元素。

折叠在某种意义上是展开（英语：Anamorphism）（unfold）的对偶，它接受一个种子值并共递归的应用一个函数，来确定如何进一步的构造一个共递归的数据结构。折叠递归的分解这个数据结构，在每个节点应用一个组合函数于它的终结值和递归结果之上，用得到这个结果替代它。折叠是catamorphism（英语：catamorphism），而展开是anamorphism（英语：anamorphism）。

作为结构性变换

折叠可以视为是将数据结构的结构性构件一致性的替代为函数和值。例如在很多函数式语言中，列表是用两个原语建造的：任何列表要么是一个空列表，通常叫做nil（[]），要么是通过将一个元素前缀于另一个列表之前来构造的，通过应用cons函数（在Haskell中写为冒号(:)），建立所谓的cons节点（英语：Node (computer science)），比如 Cons(X1,Cons(X2,Cons(...(Cons(Xn,nil)))))。可以将在列表上的折叠看作是将这个列表的末端的nil替代为一个特殊的值，并用一个特殊函数替代每个cons。

使用Haskell作为例子，可以用几个等式公式化出右折叠foldr：

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z []     = z
foldr f z (x:xs) = f x (foldr f z xs)

如果列表为空，结果是初始值z。如果不是空，应用f于第一个元素和折叠余下列表的结果。这种替代可以图示如下：

以一致性风格进行结构性变换的另一种方式，左折叠foldl：

foldl :: (b -> a -> b) -> b -> [a] -> b
foldl f z []     = z
foldl f z (x:xs) = foldl f (f z x) xs

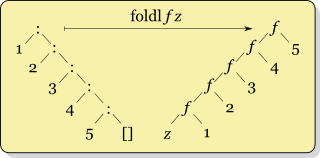
如果列表为空，结果是初始值。如果不是空，将应用f于旧初始值和第一个元素的结果作为新初始值，折叠它和余下列表。这种替代可以图示如下：

这两个示意图展示在一个列表上的右折叠和左折叠。逐个元素的使用cons构造的列表，每个节点的左链接是终结值，而右链接是另一个节点，右折叠之后保持这种形态。左折叠之后，承载函数的每个节点的右链接是终结值，而左链接是另一个节点。

这两个示意图还突出了如下事实：id = foldr (:) []是在列表上的同一函数（按Lisp说法是“浅层复制”），因为替代cons为cons并替代nil为nil不改变结果。并提示了逆转一个列表的一种容易的方法：reverse = foldl (flip (:)) []。注意这里用flip函数将给cons的二个参数进行了翻转。flip只在Haskell这样的语言中需要，它翻转给foldl的组合函数的实际参数的次序，不像在Scheme中，这里对foldl和foldr二者的组合函数使用相同的实际参数次序。

另一个易得的结果是，高阶函数map也可以凭借foldr书写，通过将要作用在元素上的那个函数复合于cons，即是：

map f = foldr ((:) . f) []

这里的点号(.)是指示函数复合（英语：Function composition (computer science)）的算子。

通过演示在线性列表上的折叠函数的构造方式，就会得到启发在其他代数数据类型和结构比如各种树之上设计类似的折叠函数。我们可以写一个高阶函数，递归的将数据类型的构造子替代为所提供的函数，并将任何这个类型的常量值替代为所提供的值。这种函数一般称为catamorphism（英语：catamorphism）。

在列表上

用加法算子折叠列表[1,2,3,4,5]会得到结果15, 它是这个列表元素的总和。粗略近似的说，折叠将这个列表中逗号替代成了+运算，得出了1 + 2 + 3 + 4 + 5。

在上述的例子中，+是结合律运算，所有最终的结果不管如何加括号都是相同的，尽管括号导致的特定计算次序是不同的。在非结合律二元运算的一般情况下，组合元素的次序可以影响最终的结果值。在列表之上，有二个面向的进行这个工作的方式：要么组合第一个元素和递归的组合余下列表的结果（叫做右折叠），要么组合递归的组合除了最后一个元素的所有元素的结果和最后一个元素（叫做左折叠）。着对应于一个二元算子要么是右结合的要么是左结合的，采用了Haskell或Prolog的术语。使用右折叠，合计将加括号为1 + (2 + (3 + (4 + 5)))，而使用左折叠它将加括号为(((1 + 2) + 3) + 4) + 5。

实际上，在使用右折叠的情况下有一个初始值同列表的最后一个元素组合，在使用左折叠的情况下有一个初始值同和列表的第一个元素组合，是方便和自然的。在上述的例子中，值0（加法单比特）可以被选择为初始值，对于右折叠得到1 + (2 + (3 + (4 + (5 + 0))))，对于左折叠得到((((0 + 1) + 2) + 3) + 4) + 5。对于乘法，选择1（乘法单比特）作为初始值，这将得出1 * 1 * 2 * 3 * 4 * 5 = 120 = 5!。

在组合函数f的类型是不对称的情况下，比如a -> b -> b，就是说如果结果的类型不同于列表元素的类型，使用初始值是必需的。要使一个线性的应用链成为可能，使用的这个初始值的类型必须同于f的结果的类型。不管是右折叠还是左折叠，它的类型都确定为组合函数的参数所预期的类型。如果第二个参数必须与结果相同类型，则f可以被看作是右结合的，如果是第一个参数则为左结合的。那些使用对称类型二元运算的折叠，它的二个参数的类型和它的结果的类型必须相同。

树状折叠

在组合函数是个原群的情况下，就是说它的类型是对称的，比如a -> a -> a，就是说结果的类型同于列表元素的类型，则可以用任意方式放置括号，因而建立嵌套子表达式的“树”，比如((1 + 2) + (3 + 4)) + 5。如果二元运算f是结合律的，则这个值将是良好定义的，就是对于任何加括号情况，都是相同的，尽管如何计算它的运算细节会是不同的。如果f是非严格求值的，这可能在性能上有重大影响。 线性折叠是面向节点的，并以一致方式对列表的每个节点进行运算；而树状折叠是面向整个列表的，并以一致方式跨越节点“群”进行运算。

列表可以按树状风格来折叠，分别对于有限和不明确定义的列表二者：

foldt :: (a -> a -> a) -> a -> [a] -> a
foldt f z []     = z
foldt f z [x]    = f x z
foldt f z xs     = foldt f z (pairs f xs)

foldi :: (a -> a -> a) -> a -> [a] -> a 
foldi f z []     = z
foldi f z (x:xs) = f x (foldi f z (pairs f xs))

pairs :: (a -> a -> a) -> [a] -> [a] 
pairs f (x:y:t)  = f x y : pairs f t
pairs _ t        = t

在foldi函数的情况下，为了避免在不明确定义的列表上失控求值，函数f必须“不总是”需求它的第二个参数的值，至少不是所有都要，或者不是立即就要。

非空列表的特殊折叠

人们经常希望选择f的单比特作为初始值z。在没有合适的初始值的时候，例如在想要把计算它的二个参数的极大值的函数，折叠到一个非空列表之上，来得到这个列表的极大值，可以用foldr和foldl的变体，它们分别使用这个列表的最后一个和第一个元素作为初始值。在Haskell和其他一些语言中，它们叫做foldr1和foldl1，这里的“1”所指的是自动提供初始元素，和它们所应用到的列表至少要有一个元素的事实。

foldl1 f [x]      = x
foldl1 f (x:y:xs) = foldl1 f (f x y : xs)

foldr1 f [x]      = x
foldr1 f (x:xs)   = f x (foldr1 f xs)

foldt1 f [x]      = x
foldt1 f (x:y:xs) = foldt1 f (f x y : pairs f xs)
 
foldi1 f [x]      = x
foldi1 f (x:xs)   = f x (foldi1 f (pairs f xs))

例子

使用Haskell解释器，折叠进行的结构性变换可以用构造一个字符串来展示：

λ> foldr (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(1+(2+(3+(4+(5+(6+(7+(8+(9+(10+(11+(12+(13+0)))))))))))))"
 
λ> foldl (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(((((((((((((0+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)+11)+12)+13)"
 
λ> foldt (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(((((1+2)+(3+4))+((5+6)+(7+8)))+(((9+10)+(11+12))+13))+0)"
 
λ> foldi (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(1+((2+3)+(((4+5)+(6+7))+((((8+9)+(10+11))+(12+13))+0))))"

无限树状折叠，可以用Haskell的通过埃拉托斯特尼筛法的递归素数生成来演示：

primes = 2 : _Y ((3 :) . minus [5,7..] . foldi (\(x:xs) ys -> x : union xs ys) [] 
                       . map (\p-> [p*p, p*p+2*p..]))
_Y g = g (_Y g)     -- = g . g . g . g . ...

这里的函数union以本地方式运算于有序列表之上来高效的产生它们的并集，而minus 做它们的集合差。

对于有限列表，归并排序（和它的去除重复变体nubsort）可以使用树状折叠轻易的定义为：

mergesort xs = foldt merge [] [[x] | x <- xs]
nubsort   xs = foldt union [] [[x] | x <- xs]

采用的函数merge是union的保留重复的变体。

函数head和last也可以通过折叠定义为：

head = foldr (\x r -> x) (error "head: Empty list")
last = foldl (\a x -> x) (error "last: Empty list")

求值次序考虑

在采用惰性或非严格求值策略的场合下，foldr将立即返回f在列表头部和折叠余下列表的递归案例上的这个应用。因此，如果f能够产生其结果的一部分，而不需要引用到递归案例，它在f的“右”也就是第二个实际参数上，而余下的结果永不需要，那么递归就会停止，例如上节定义的head函数。这允许右折叠可以运算在无限列表之上。与之相反，foldl将立即的调用具有新参数的自身，直到它达到了列表的末端。这种尾递归可以高效的编译为循环，但是根本不能处理无限列表，它会永久递归于无限循环。

已经到达列表的末端之后，foldl有效的建造了一个“表达式”，它是嵌套的左深化f应用，它被提供给调用者进行求值。如果函数f首先引用它的第二个参数，并且能够产生其结果的一部分，而不需要引用到递归案例，这里是在它的“左”也就是第一个实际参数上，那么递归会停止，例如上节定义的last函数。这意味着尽管foldr递归“于右侧”，它允许惰性组合函数来从左至右检查列表的元素；而反过来，尽管foldl递归“于左侧”，它允许惰性组合函数从从右至左检查列表的元素。

逆转一个列表也是尾递归的，它可以使用rev = foldl (\ys x -> x : ys) []实现。在有限列表上，这意味着左折叠和逆转可以复合起来以尾递归方式进行右折叠，通过修改f使它逆转其参数的次序，例如foldr f z == foldl (flip f) z . rev，这样尾递归的建造出的一个表达式的表示同于右折叠所建造的。

额外的中间列表结构可以通过形似传递续体风格（英语：continuation-passing style）的手段去除：foldr f z xs == foldl (\k x-> k . f x) id xs z；另一个在也类似：foldl f z xs == foldr (\x k-> k . flip f x) id xs z。它们也常被写为^[1]：

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z xs = foldl (\k x y -> k (f x y)) id xs z

foldl :: (b -> a -> b) -> b -> [a] -> b
foldl f z xs = foldr (\x k y -> k (f y x)) id xs z

另一个技术要点是，在使用惰性求值的左折叠的情况下，新初始化参数在进行递归调用之前是不被求值的。在达到了列表末端并尝试计算结果的巨大的表达式的时候，这可能导致堆栈溢出。为此，这种语言经常提供左折叠的更严格变体，它在进行递归调用之前强制的求值初始化参数。在Haskell中它是Data.List库里的foldl'函数（注意这个撇号读作“prime”）。需要意识到一个事实，强制一个值用惰性数据构造子建造，其自身不会自动的强制它的构件。结合于尾递归，这种折叠接近了循环的效率，在惰性求值的最终结果是不可能或不可取的时候，确保了恒定空间运算。

在各种语言中

语言	左fold	右fold	无初始值左fold	无初始值右fold	Unfold	注释
APL	func⍨/⌽initval,vector	func/vector,initval	func⍨/⌽vector	func/vector
C# 3.0	ienum.Aggregate(initval, func)	ienum.Reverse().Aggregate(initval, func)	ienum.Aggregate(func)	ienum.Reverse().Aggregate(func)		Aggregate是扩展方法（英语：Extension method） ienum是IEnumerable<T> 在所有的.NET语言中都类似
C++	std::accumulate(begin, end, initval, func)	std::accumulate(rbegin, rend, initval, func)				在头文件 <numeric>中 begin, end, rbegin, rend是迭代器 func可以是一个函数指针或函数对象
C++17	(initval op ... op pack)	(pack op ... op initval)	(... op pack)	(pack op ...)		Fold表达式（只用于变元函数模板）：op是二元算子（两个op必须相同，比如(std::cout << ... << args))， pack是未展开的参数包。
CFML（英语：ColdFusion Markup Language）	obj.reduce(func,initial)		obj.reduce(func)			这里的func接受为实际参数的是前面运算的结果（或在第一次迭代上的initial值）；当前项；当前项的索引或键；和到obj的引用。
Clojure	(reduce func initval list)	(reduce func initval (reverse list'))	(reduce func list)	(reduce func" (reverse list))		参见clojure.core.reducers/fold[2]
Common Lisp	(reduce func list :initial-value initval)	(reduce func list :from-end t :initial-value initval)	(reduce func list)	(reduce func list :from-end t)
Curl	{{TreeNode.default treeNode ...} .to-Iterator}	{{TreeNode.default treeNode ...} .reverse}.to-Iterator}	{for {treeNode.to-Iterator} do}	{for {{treeNode.reverse}.to-Iterator} do}		还有DefaultListModel和HashTable实现to-Iterator
D	reduce!func(initval, list)	reduce!func(initval, list.reverse)	reduce!func(list)	reduce!func(list.reverse)		在模块std.algorithm中
Elixir	List.foldl(list, acc, fun)	List.foldr(list, acc, fun)				样例用法见于documentation[3]
Elm	List.foldl(Fun, Accumulator, List)	List.foldr(Fun, Accumulator, List)				参见List API[4]
Erlang	lists:foldl(Fun, Accumulator, List)	lists:foldr(Fun, Accumulator, List)
F#	Seq/List.fold func initval list	List.foldBack func list initval	Seq/List.reduce func list	List.reduceBack func list	Seq.unfold func initval
Gosu（英语：Gosu (programming language)）	Iterable.fold(f(agg, e))Iterable.reduce(init, f(agg, e)) Iterable.partition(f(e))					都是在java的Iterable接口上的扩展方法（英语：extension methods），数组也支持。
Groovy	list.inject(initval, func)	list.reverse().inject(initval, func)	list.inject(func)	list.reverse().inject(func)
Haskell	foldl func initval list	foldr func initval list	foldl1 func list	foldr1 func list	unfoldr func initval	对于foldl，折叠函数接受参数的次序与foldr的次序相反。
Haxe	Lambda.fold(iterable, func, initval)
J	verb~/|. initval,array	verb/ array,initval	verb~/|. array	verb/ array		u/y应用二元u于y的项目之间。参见"J Dictionary: Insert"[5]
Java 8+	stream.reduce(initval, func)		stream.reduce(func)
JavaScript 1.8 ECMAScript 5	array.reduce(func, initval)	array.reduceRight(func, initval)	array.reduce(func)	array.reduceRight(func)
Julia	foldl(op, itr; [init])	foldr(op, itr; [init])	foldl(op, itr)	foldr(op, itr)
Kotlin	Iterable.fold(initval, func)	Iterable.foldRight(initval, func)	Iterable.reduce(func)	Iterable.reduceRight(func)		其他搜集也支持fold[6]和reduce[7]。还有Result.fold(onSuccess, onFailure)[8]，它归约Result<T>（要么成功要么失败）成onSuccess和onFailure的返回类型。
LFE（英语：LFE (programming language)）	(lists:foldl func accum list)	(lists:foldr func accum list)
Logtalk（英语：Logtalk）	fold_left(Closure, Initial, List, Result)	fold_right(Closure, Initial, List, Result)				meta标准库对象提供元谓词。缩写foldl和foldr也可以使用。
Maple	foldl(func, initval, sequence)	foldr(func, initval, sequence)
Mathematica	Fold[func, initval, list]	Fold[func, initval, Reverse[list]]	Fold[func, list]	Fold[func, Reverse[list]]	NestWhileList[func,, initval, predicate]	不带初始值的Fold在版本10.0和更高版本中支持。
MATLAB	fold(@func, list, defaultVal)	fold(@func, flip(list), defaultVal)	fold(@func, list)	fold(@func, flip(list))		要求Symbolic Math Toolbox，从R2016b开始支持。
Maxima	lreduce(func, list, initval)	rreduce(func, list, initval)	lreduce(func, list)	rreduce(func, list)
Mythryl	fold_left func initval list vector::fold_left func initval vector	fold_right func initval list vector::fold_right func initval vector				提供的函数接受在元组中实际参数。
OCaml	List.fold_left func initval list Array.fold_left func initval array	List.fold_right func list initval Array.fold_right func array initval			Base.Sequence.unfold ~init ~f [9]
Oz	{FoldL List Func InitVal}	{FoldR List Func InitVal}
PARI/GP（英语：PARI/GP）	fold( f, A )
Perl	reduce block initval, list		reduce block list			在List::Util模块中
PHP	array_reduce(array, func, initval)	array_reduce(array_reverse(array), func, initval)	array_reduce(array, func)	array_reduce(array_reverse(array), func)		在未提供initval的时候，使用了NULL，所以不是真正的foldl1。在PHP 5.3之前，initval只能是整数。func是一个callback[10]。参见在线的array_reduce文档[11]。
Python 2.x	reduce(func, list, initval)	reduce(lambda x,y: func(y,x), reversed(list), initval)	reduce(func, list)	reduce(lambda x,y: func(y,x), reversed(list))
Python 3.x	functools.reduce(func, list, initval)	functools.reduce(lambda x,y: func(y,x), reversed(list), initval)	functools.reduce(func, list)	functools.reduce(lambda x,y: func(y,x), reversed(list))		在模块functools中[12]。
R	Reduce(func, list, initval)	Reduce(func, list, initval, right=TRUE)	Reduce(func, list)	Reduce(func, list, right=TRUE)		R通过给Reduce函数的right和init实际参数，支持右折叠和有或没有初始值的左或右折叠。
Ruby	enum.inject(initval, &block) enum.reduce(initval, &block)	enum.reverse_each.inject(initval, &block) enum.reverse_each.reduce(initval, &block)	enum.inject(&block) enum.reduce(&block)	enum.reverse_each.inject(&block) enum.reverse_each.reduce(&block)		在Ruby 1.8.7+中，还可以传递表示一个函数而非块的一个符号。 enum是Enumeration 请注意这些右折叠的实现对于非交换律的&block是有误的（还有初始值放在错误的一侧）。
Rust	iterator.fold(initval, func)	iterator.rev().fold(initval, func)
Scala	list.foldLeft(initval)(func) (initval /: list)(func)	list.foldRight(initval)(func) (list :\ initval)(func)	list.reduceLeft(func)	list.reduceRight(func)		Scala的符号式fold语法意图重组常用来解释折叠运算的左或右倾斜树[13]，已经被重释义为一个顶级多米诺骨牌的例证[14]。来自通用Scala语法机制的冒号，凭借显见的中缀算子，被调用为一个方法在左操作数上，具有右操作数作为一个实际参数传递，或反之如果这个算子的最后字符是冒号，这里是对称应用的。 Scala还有使用方法list.fold(z)(op)的树状折叠特征[15]。
Scheme R6RS	(fold-left func initval list) (vector-fold func initval vector)	(fold-right func initval list) (vector-fold-right func initval vector)	(reduce-left func defaultval list)	(reduce-right func defaultval list)		srfi/1 srfi/43
Smalltalk	aCollection inject: aValue into: aBlock		aCollection reduce: aBlock			ANSI Smalltalk不定义#reduce: 但是很多实现定义了。
Standard ML	foldl func initval list Array.foldl func initval array	foldr func initval list Array.foldr func initval array				提供的函数接受在元组中的实际参数。对于foldl，折叠函数接受实际参数的次序同于foldr的次序。
Swift	array.reduce(initval, func) reduce(sequence, initval, func)	array.reverse().reduce(initval, func)
XPath 3.1	array:fold-left( $array as array(*), $zero as item()*, $f as function(item()*, item()*) as item()*) as item()*[16] fold-left( $seq as item()*, $zero as item()*, $f as function(item()*, item()) as item()*) as item()*[17]	array:fold-right( $array as array(*), $zero as item()*, $f asfunction(item()*, item()*) as item()*) as item()*[18] fold-right( $seq as item()*, $zero as item()*, $f as function(item(), item()*) as item()*) as item()*[19]				在XPath 3.1中由于历史原因，array和sequence类型是不兼容的 -- 因此需要分离给array和给sequence的fold函数。在签名上的不同是由于array项目的值可以是sequence，但是XPath没有sequence的sequence。
Xtend（英语：Xtend）	iterable.fold(initval,[func])		iterable.reduce[func]

普遍性

折叠是多态函数。对于有如下这样定义的任何g：

g [] = v
g (x:xs) = f x (g xs)

g都可以表达为^[20]：

g = foldr f v

还有，不动点组合子可以通过折叠实现^[21]，证明迭代可以被归约成折叠：

y f = foldr (\_ -> f) undefined (repeat undefined)

参见

• 聚集函数（英语：Aggregate function）
• 迭代二元关系（英语：Iterated binary operation）
• Map (高阶函数)
• Filter (高阶函数)
• 前缀和（英语：Prefix sum）
• 递归数据类型
• 递归算子（英语：Reduction Operator）
• 递归 (计算机科学)