模版 (数值分析)

在数学的偏微分方程数值方法里，模版（stencil）是有关几何安排的资讯，会用在一个点周围点上的资讯来求得所关注点的资讯。模版是许多求解偏微分方程（PDE）数值方法演算法的基础。五点模版和克兰克-尼科尔森方法模版就是模版的例子。

一维问题克兰克-尼科尔森方法的模版

模版可分为两类：紧致模版（英语：Compact stencil）和非紧致模版（英语：Non-compact stencil），两者的差异在只利用关注点邻近的点，或是会用到更远处的点。

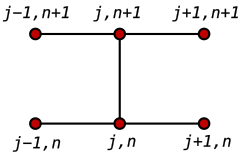
在一维模版中，会用n-1、n和n+1表示时间的步阶，其中n和n-1是数值已知的，而有限体积空间上的分布会表示为j-1、j和j+1。

名称

在偏微分方程研究的早期，就已有用图示表示所使用节点和系数的作法，当时的名称有relaxation patterns、operating instructions、lozenges或point patterns等^[1][2]。后来将此名称取名为"模版"（stencil），是将模板喷画中模板的概念用在数值方法求解时，用图示表示在特定一步需要其他哪些点的资讯^[2]。

系数计算

偏微分方程数值方法中，确定方法和模版后，其有限差分系数就固定了，此系数可用拉格朗日多项式在这些点之间内插，再微分求得^[3]，作法是计算附近每个点的泰勒级数，再求解方程式^[4]，或是强制该模式就符合最多到模版阶数的单项式^[3]。

相关条目

• 紧致模版（英语：Compact stencil）
• 非紧致模版（英语：Non-compact stencil）
• 五点模版
• 九点模版（英语：Nine-point stencil）
• 迭代模版循环（英语：Iterative Stencil Loops）