数学上,两个集合 和
和 的交集是含有所有既属于
的交集是含有所有既属于 又属于
又属于 的元素,而没有其他元素的集合。
的元素,而没有其他元素的集合。
有限交集
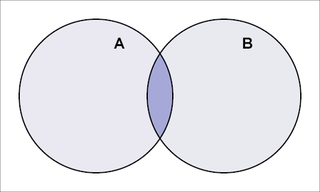 A和
A和 的交集
的交集
交集是由公理化集合论的分类公理来确保其唯一存在的特定集合  :
:
![{\displaystyle (\forall A)(\forall B)(\forall x)\left\{(x\in A\cap B)\Leftrightarrow \left[(x\in A)\wedge (x\in B)\right]\right\}}](//wikimedia.org/api/rest_v1/media/math/render/svg/54360e98d87681f93515678a7bf5f38a8388f0b4)
也就是直观上:
 和
和 的交集写作“
的交集写作“ ”,“对所有
”,“对所有  ,
,  等价于
等价于  且
且  ”
”
例如:集合 和
和 的交集为
的交集为 。数字
。数字 不属于素数集合
不属于素数集合 和奇数集合
和奇数集合 的交集。
的交集。
若两个集合 和
和 的交集为空,就是说它们彼此没有公共元素,则他们不相交,写作:
的交集为空,就是说它们彼此没有公共元素,则他们不相交,写作: 。例如集合
。例如集合 和
和 不相交,写作
不相交,写作 。
。
更一般的,交集运算可以对多个集合同时进行。例如,集合 ,
, 和
和 的交集为
的交集为 。交集运算满足结合律。即:
。交集运算满足结合律。即:

任意交集
以上定义可根据无限并集和补集来推广到任意集合的交集。
取一个集合  ,则根据分类公理可以取以下唯一存在的集合:
,则根据分类公理可以取以下唯一存在的集合:
 。
。
也就是直观上搜集所有  的集合, 这样的话有:
的集合, 这样的话有:
![{\displaystyle x\in \bigcup {\bar {\mathcal {M}}}\Leftrightarrow (\exists A)[(x\in A)\wedge (\exists M\in {\mathcal {M}})(A=M^{c})]}](//wikimedia.org/api/rest_v1/media/math/render/svg/d67866579140d60b65b1b975dc70004e12e318d1)
根据一阶逻辑的定理(Ce),也就是:
![{\displaystyle x\in \bigcup {\bar {\mathcal {M}}}\Leftrightarrow (\exists M)[(M\in {\mathcal {M}})\wedge (x\notin M)\wedge (\exists A)(A=M^{c})]}](//wikimedia.org/api/rest_v1/media/math/render/svg/1899bfcbe3c6795e5a1dedb68d10caf7217fdd51)
但根据一阶逻辑的等式相关定理,下式:

显然是个定理(也就是直观上为真),故:

换句话说:

那可以做如下的符号定义:

称为  的任意交集或无限交集。也就是直观上“对所有
的任意交集或无限交集。也就是直观上“对所有  ,
,  等价于对任何
等价于对任何  的下属集合
的下属集合  ,都有
,都有  ”
”
例如:

类似于无限并集,无限交集的表示符号也有多种
可模仿求和符号记为
 。
。
但大多数人会假设指标集  的存在,换句话说
的存在,换句话说
- 若
 则
则 
在指标集  是自然数系
是自然数系  的情况下,更可以仿无穷级数来表示,也就是说:
的情况下,更可以仿无穷级数来表示,也就是说:
- 若
 则
则 
也可以更粗略直观的将  写作
写作 。
。
参见





 的交集
的交集
























。







。

则


则


![{\displaystyle (\forall A)(\forall B)(\forall x)\left\{(x\in A\cap B)\Leftrightarrow \left[(x\in A)\wedge (x\in B)\right]\right\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/54360e98d87681f93515678a7bf5f38a8388f0b4)


![{\displaystyle x\in \bigcup {\bar {\mathcal {M}}}\Leftrightarrow (\exists A)[(x\in A)\wedge (\exists M\in {\mathcal {M}})(A=M^{c})]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d67866579140d60b65b1b975dc70004e12e318d1)
![{\displaystyle x\in \bigcup {\bar {\mathcal {M}}}\Leftrightarrow (\exists M)[(M\in {\mathcal {M}})\wedge (x\notin M)\wedge (\exists A)(A=M^{c})]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1899bfcbe3c6795e5a1dedb68d10caf7217fdd51)









