热门问题
时间线
聊天
视角
二面體群
来自维基百科,自由的百科全书
Remove ads
在數學中,二面體群 是正 邊形的對稱群,具有 個元素。某些書上則記為 。除了 的情形外, 都是非交換群。
此條目沒有列出任何參考或來源。 (2009年6月15日) |

Remove ads
生成元與關係
抽象言之,首先考慮 階循環群 。反射 是 上的自同構,而且 。定義二面體群為半直積
任取 的生成元 , 由 生成,其間的關係是
的元素均可唯一地表成 ,其中 ,。
Remove ads
幾何詮釋


二面體群也可以詮釋為二維正交群 中由
- (旋轉 弧度)
- (對 x 軸反射)
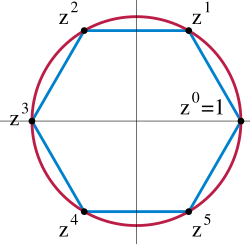
生成的子群。由此不難看出 是正 n 邊形的對稱群。
Remove ads
性質
- 的中心在 為奇數時是 ,在 為偶數時是 。
- 當 為奇數時, 同構於 與二階循環群的直積。同構可由下式給出:
其中 ,。
Remove ads
表示
當 為奇數時, 有兩個一維不可約表示:
當 為偶數時, 有四個一維不可約表示:
其餘不可約表示皆為二維,共有 個,形如下式:
其中 是任一 n 次本原單位根, 過 。由 給出的表示相等價若且唯若 。
Remove ads
文獻
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads