病態 (數學)

在數學中，病態（英語：Pathological）現象是指其性質被認為是非典型的或反直覺的現象，反義詞為良態（Well-behaved）。

魏爾斯特拉斯函數是無處不連續的，但任何一處都不可微

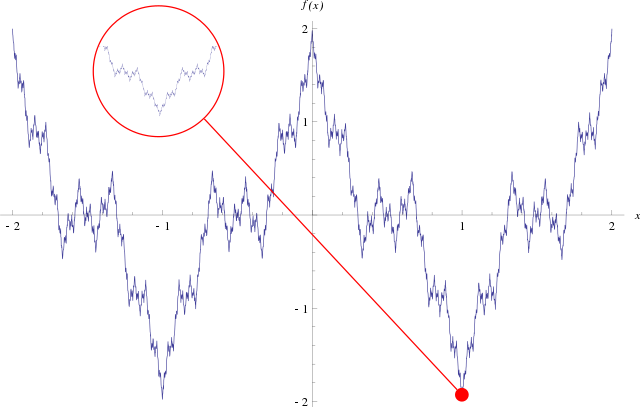
在分析學中

一個經典的例子的病態結構是魏爾斯特拉斯函數，它處處連續但處處不可微。可微函數和魏爾斯特拉斯函數的總和也是連續的，但是無處可微；所以這種函數至少與可微函數一樣多。事實上，由貝爾綱定理之一可以顯示，連續函數通常是無處可微的。

通俗地說，大多數函數都不可微，而且相對較少的函數可以被描述或研究。一般而言，大多數實用的函數也具有某種物理基礎或實際應用，這意味著它們在理論數學或邏輯層面上不能是病態的；如果沒有像狄拉克δ函數那樣的某些限制性情況，它們往往表現得非常常態，直觀。引用龐加萊的話：

有時，邏輯生出妖怪。近半世紀，怪誕的函數異軍突起，竭力標奇立異，與實際有用的函數大相逕庭。其不再連續，甚或連續但不可導，如此種種。誠然，以邏輯觀之，該等怪異函數纔是最普遍；相反，以簡單法則定義，無需刻意尋找的函數，反倒是特例，僅佔牆隅立錐之地。

以前，發明新函數，是為實用；今時，則祗為刻意突顯先賢的邏輯缺陷，此外別無他用。

師者若祗以邏輯為綱領，則必由最普遍的函數開始教授，亦即最怪異的函數。如此，學生初學已須勉強面對整座畸形學博物館（musée tératologique）；否則，邏輯學家會挑剔你僅逐步邁向嚴謹。

——Henri Poincaré^[1]，1899

這突出表明，該術語「病態」是主觀的，依賴於語境，並且正在逐漸消失。它在任何特定情況下的含義都存在於數學家群體中，而不一定在數學本身中。此外，引文顯示數學經常如何通過反例進展到直覺或預期結果；例如所提到的「不可導」與目前對太陽電漿體中磁重聯事件的研究密切相關。

在拓撲學中

拓撲學中最臭名昭著的病態之一是亞歷山大帶角球（英語：Alexander horned sphere），這是一個反例，表明拓撲將球體S²嵌入R³中可能無法完全分離空間。作為反例，它激發了馴服（tameness）的額外條件，這抑制了帶角球所表現出的野性行為。

像許多其他病態一樣，帶角球在某種意義上是無限精細的遞迴生成結構，在極限情況下違反了普通的直覺。在這種情況下，在極限範圍內連續的球體互鎖環的不斷下降的鏈的拓撲結構完全反映了普通球體的拓撲結構，而期望值在嵌入之後它的外部表現相同。然而事實卻並非如此：它沒有單連通。

對於基礎理論，請參閱喬登-薛弗利斯定理（英語：Schoenflies problem）。

在線性代數中

定義：如果線性方程組${\displaystyle Ax=b}$ 中，A或b的元素的微小變化，會引起方程組解的巨大變化，則稱方程組為病態方程組，稱矩陣A為病態矩陣。條件數可以用來衡量方程組的「病態」程度。^[2]

一種常見的病態矩陣是n階希爾伯特矩陣，隨著階數n的增大，而呈現嚴重的病態。^[2]

良態

數學家（以及相關科學家）經常談論一個數學物件（函數、集合，或任何空間）是否良態。該術語沒有固定的正式定義，而是取決於背景、數學興趣、時尚和品味。為了確保物件處在良態，數學家引入了進一步的公理來縮小研究領域。這有利於使分析更容易，但減少了所得結論的一般性。像非歐幾何這樣的概念曾被認為是不正常的，但現在已成為常見的研究物件。

在純數學和應用數學（例如最佳化、數值積分或數學物理學）中，良態也意味著研究對象滿足目前分析適用所需的一切假設。

相反的情況通常標記為病態的。在（基數或測度意義下）大多數例子中，這種病態情況並不罕見，但除非故意構建，否則病態情況不會在實踐中出現。

術語「表現良好」（或良態）通常用於絕對意義上——要麼表現得好，要麼反之。例如：

• 在算法推理（英語：Algorithmic inference）中，表現良好的統計量（英語：Well-behaved statistic）是單調的、明確定義的和充分的。
• 在貝祖定理中，如果兩個多項式的多項式最大公因數是常數，它們的交點數定理給出的公式是有效的，它們表現良好。
• 亞純函數是兩個表現良好的函數的比，指的是這兩個函數是全純的。
• 卡羅需－庫恩－塔克條件是一個表現良好的非線性規劃問題解決方案最優的一階必要條件；如果滿足一些規律性條件，則問題被稱為表現良好。
• 在機率上，機率空間對應的Σ-代數中包含的事件表現良好，可測函數也是如此。

雖然較少見，但該術語也可以比較方式使用：

• 在微積分中：
  • 解析函數比一般光滑函數表現得更好。
  • 平滑函數比一般可微函數表現更好。
  • 連續可微函數比一般連續函數表現更好。函數可以微分的次數越多，它的表現就越好。
  • 連續函數比稠密集上的黎曼可積函數表現更好。
  • 黎曼可積函數比勒貝格可積函數表現更好。
  • 勒貝格可積函數比一般函數表現更好。
• 在拓撲中，連續函數比不連續函數表現得更好。
  • 歐幾里德空間比非歐幾里德幾何更好。
  • 吸引不動點比排斥不動點更好。
  • 郝斯多夫空間比任意點集拓撲中的拓撲更好。
  • 鮑萊耳集比任意實數集合表現更好。
  • 具有整數維度的空間比具有碎形維度的空間表現得更好。
• 在抽象代數中：
  • 群比原群和半群更好。
  • 阿貝爾群表現得比非阿貝爾群更好。
  • 有限生成阿貝爾群比非有限生成交換群表現更好。
  • 有限維向量空間比無限維向量空間更好。
  • 域比除環或一般環更好。
  • 可分離的體擴張比不可分離的體擴張更好。
  • 賦範除法代數比一般組合代數表現得更好。

病態實例

病態的實例通常具有一些不合乎需要或不尋常的特性，所以難以在理論中包含或解釋。這種病態行為常常引發新的研究，從而產生新的理論和更一般的結果。例如，一些重要的歷史例子如下：

• 古希臘畢達哥拉斯學派發現的無理數；例如，單位正方形的對角線的長度，即${\displaystyle {\sqrt {2}}}$。
• 有理數的基數等於整數的基數。
• 某些代數數體的整數環無唯一分解，例如域${\textstyle \mathbb {Q} ({\sqrt {-5}})}$。
• 碎形和其他「粗糙」幾何物件的發現（參見郝斯多夫維數）。
• 魏爾施特拉斯函數，一個在實直線上的實數值函數，它在任何地方都是連續的，但在任何地方都不是可微分的。
• 實際分析和分布理論中的測試函數，它們是實直線上的無限可微函數，在給定的有限區間之外的任何地方都是0。這種函數的一個例子是測試函數，${\textstyle \varphi (t)={\begin{cases}e^{-1/(1-t^{2})},&{\text{若 }}-1<t<1,\\0,&{\text{其 他 情 況 }}\ \ .\end{cases}}}$
• 康托爾集是區間[0, 1]的零測度子集，但不可數。
• 皮亞諾曲線是一個將區間[0, 1]映射到[0, 1] × [0, 1]的連續的滿射函數。
• 有理數的指標函數有界但處處不連續，且不是黎曼可積的。
• 康托爾函數是一個單調的連續映射，它將[0,1]映射到[0,1]，但幾乎處處導數為零。
• 可以為皮亞諾算術的可數遞迴飽和模型構建包含滿足「直觀錯誤」算術語句的類。^{[來源請求]}

在它們被發現時，這些實例被認為是高度病態的；今天，每個實例都被同化為現代數學理論了。這些例子促使他們的觀察者糾正他們的信仰或直覺；有時他們甚至可能需要重新評估基本定義和概念。在歷史的過程中，它們導致了更正確，更精確，更強大的數學。例如，狄利克雷函數是勒貝格可積的，而測試函數的摺積適用於求出任何局部可積函數的平滑擬合（此處擬合是在局部可積函數的空間中，幾乎處處意義下）。

根據定義，行為是否是病態的，取決於個人的直覺。病態依賴於背景、培訓和經驗——一個研究人員看來是病態，很可能另一個人看來表現良好。

病態的例子可以說明假設在一個定理中的重要性。例如，在統計學中，即使柯西分布的對稱鐘形看起來與許多分布相似，它也不滿足中央極限定理；其平均值和標準偏差不存在（或非有限），所以不滿足定理的假設。

一些最著名的悖論如巴拿赫-塔斯基悖論和郝斯多夫悖論都基於不可測集的存在性。除非他們採取少數立場否認選擇公理，不然數學家一般都只能接受這些集合存在。^{[來源請求]}

計算機科學

在計算機科學中，「病態」對算法的研究略有不同。這裡，如果輸入（或輸入集合）引起來自算法的非典型行為，例如違反其平均情況複雜性或甚至其正確性，則稱輸入（或輸入集合）是病態的。例如，哈希表通常具有病態輸入：在哈希值上碰撞的鍵組。快速排序通常具有O(n log n)時間複雜度，但是當給定輸入觸發次優行為時惡化為O(n² )。

這個術語經常作為一種拒絕輸入的方式作貶義使用，例如被專門設計來打破一個在實踐中聽起來很正常的慣例（與拜占庭將軍問題比較）。另一方面，對病態輸入的認識很重要，因為它們可被利用來對計算機系統進行拒絕服務攻擊。此外，這個意義上的術語與其他意義一樣是主觀判斷的問題。如果有足夠的運行時間，足夠大和多樣化的用戶群或其他因素，實際上可能會發生可被視為病態的輸入（如在亞利安5號的第一次試飛中所見）。

特殊情況

一個類似但不同的現象是特殊物件（和異常的同構），當一般模式存在「少量」例外時——一定量地，對於無限規則的有限的例外集合。相比之下，在病態的情況下，通常大多數或幾乎所有的現象都是病態的，如普遍存在的那樣，例如幾乎所有的實數都是無理數。

主觀上，特殊情況（例如二十面體或散在群）通常被認為是「美麗的」，一個理論的意外例子。而病態現象顧名思義通常被認為是「醜陋的」。因此，理論通常擴展到包括特殊物件——例如，單李代數被包含在半單李代數理論中：公理被認為是好的，特殊物件是意外但有效的。相比之下，病態的例子被用來指出公理中的一個缺點，需要更強的公理來排除它們 - 例如，要求在Schönflies問題中嵌入球體的馴化。人們可以研究更一般的理論，包括可以提供其自身簡化的病態（實數具有與有理數非常不同的屬性，同樣連續映射具有與平滑映射非常不同的屬性），但也將在一般情況下研究狹義的理論，從中得出原始的例子。