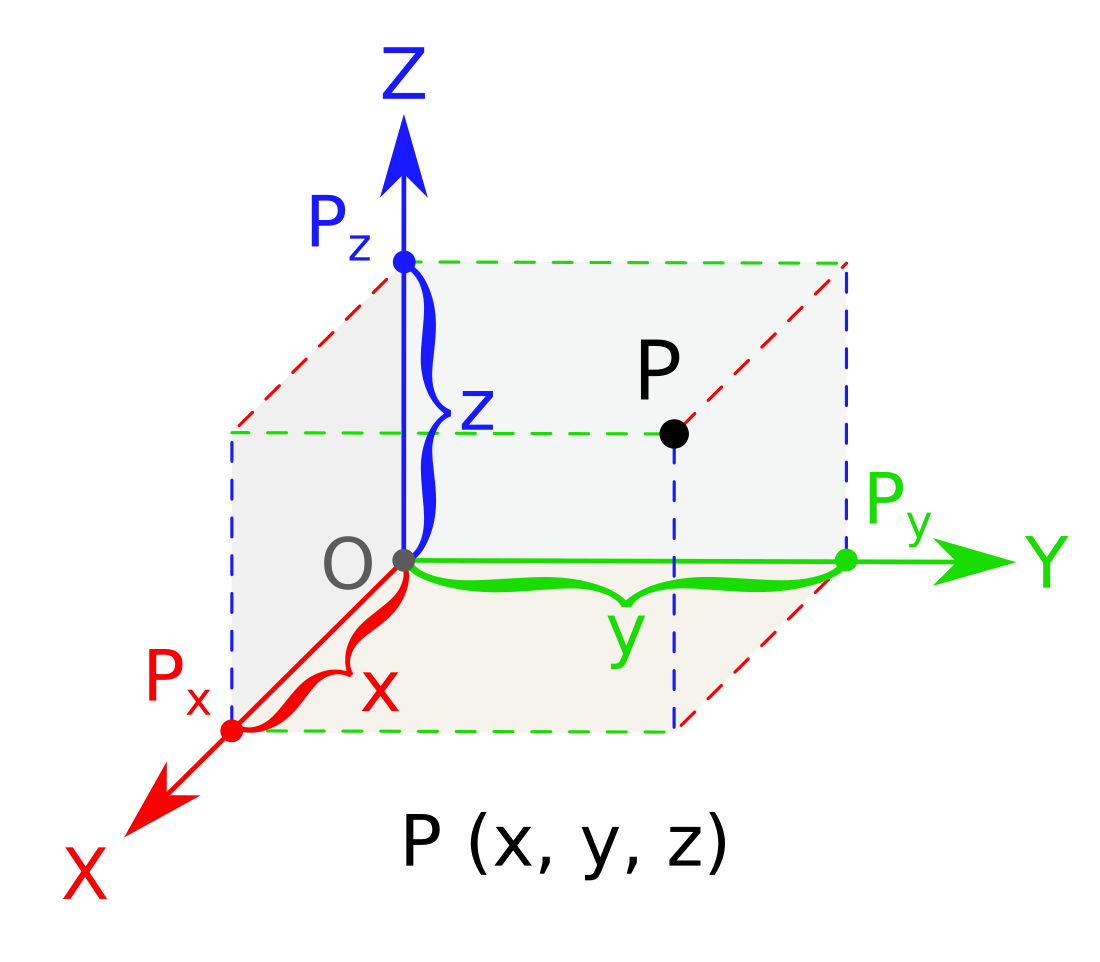
En geometria i anàlisi matemàtica, un objecte o ens és tridimensional si té tres dimensions, és a dir, cadascun dels seus punts pot ser localitzat especificant tres nombres dins d'un cert rang. Per exemple, amplada, longitud i profunditat.[1]

L'espai al nostre voltant és tridimensional a simple vista, però en realitat hi ha més dimensions, de manera que també pot ser considerat un espai tetradimensional si hi incloem el temps com a quarta dimensió.
Història
Els llibre XI, XII i XIII dels Elements d'Euclides versen sobre la geometria tridimensional. El llibre XI desenvolupa nocions d'ortogonalitat i paral·lelisme de línies i plans, i defineix sòlids que inclouen paral·lelepípedes, piràmides, prismes, esferes, octaedres icosaedres i dodecaedres. El llibre XII desenvolupa nocions de semblança entre sòlids. El llibre XIII descriu la construcció dels cinc sòlids platònics regular en una esfera.
En el segle XVII, l'espai tridimensional va ser descrit amb coordenades cartesianes, amb l'adveniment de la geometria analítica desenvolupada per René Descartes en la seva obra Geometria i per Pierre de Fermat en el seu manuscrit Ad locos planos et solidos isagoge (Introducció als llocs geomètrics plan i sòlids), inèdit en vida de Fermat. No obstant això, només l'obra de Fermat tractava de l'espai tridimensional.
En el segle XIX, els desenvolupament de la geometria de l'espai tridimensional van arribar amb l'estudi dels quaternions de William Rowan Hamilton. De fet, va ser Hamilton qui va encunyar els termes d'escalar i vector, que es van definir per primer cop dins del marc geomètric per als quaternions. L'espai tridimensional podria llavors ser descrit per quaternions que tenien un components escalar que desapareix, és a dir, . Si bé Hamilton no ho va estudiar explícitament, aquest desenvolupament va introduir indirectament nocions de base, aquí donades pels elements de quaternió , així com el el producte escalar i el producte vectorial, que corresponen a (el negatiu de) la part escalar i la part vectorial del producte de dos quaternions vectorials.
No va ser fins a Josiah Willard Gibbs, que aquests productes es van identificar per dret propi, i la notació moderna per al producte punt i creu es va introduir en les seves notes d'ensenyament a l'aula, que també es troben en el llibre de text de 1901 Vector Analysis escrit per Edwin Bidwell Wilson basat en les conferències de Gibbs.
També durant el segle XIX, es van produir desenvolupaments en el formalisme abstracte dels espais vectorials, amb l'obra de Hermann Grassmann i Giuseppe Peano, l'últim dels quals va donar per primer cop la definició moderna dels espais vectorials com a estructura algebraica.
Espai físic tridimensional
En un espai euclidià convencional, un objecte físic finit està contingut dins d'un ortoedre mínim, les dimensions es diuen ample, llarg i profunditat. L'espai físic al nostre voltant és tridimensional a simple vista.[2][3] No obstant això, quan es consideren fenòmens físics com la gravetat, la teoria de la relativitat ens porta a veure que l'univers és un ens tetradimensional que inclou tant dimensions espacials, com el temps, com una altra dimensió. Diferents observadors perceben diferents "seccions espacials" d'aquest espaitemps, per la qual cosa l'espai físic és una mica més complex que un espai euclidià tridimensional.
No es coneix exactament per què el nostre univers sembla tridimensional; més exactament, en les teories actuals no hi ha una raó clara de per què el nombre de dimensions espacials extenses (no compactificades) és igual a tres, encara que existeixen certes intuïcions sobre això: Ehrenfest va assenyalar que en quatre o més dimensions les òrbites planetàries tancades, per exemple, no serien estables (i, per tant, sembla difícil que en un univers així existís vida intel·ligent preguntant per la tridimensionalitat espacial de l'univers). També se sap que hi ha una connexió entre la intensitat d'un camp de forces estàtic amb simetria esfèrica, que satisfà el teorema de Gauss, i la dimensió de l'espai (d), un camp gravitatori, electroestàtic o d'un altre tipus que compleixi aquestes condicions. Per a grans distàncies ha de tenir una variació de la forma:
En què:
- és la intensitat del camp.
- és una constant de proporcionalitat ( per al camp gravitatori).
- és una magnitud extensiva que mesura la capacitat de font per provocar el camp, per a un camp gravitatori coincideix amb la massa i per a un d'elèctric amb la càrrega.
- és la distància al "centre" o font que crea el camp.
- és la dimensió de l'espai.
També, les teories físiques de tipus Kaluza-Klein com les diferents versions de la teoria de cordes, postula que hi ha un nombre de dimensions addicionals compactificades, que només serien observables en experiments amb partícules altament energètiques. En aquestes teories, algunes de les interaccions fonamentals poden ser explicades de manera senzilla postulant dimensions addicionals d'una manera similar a com la relativitat general explica la gravetat. De fet, la proposta original de Theodor Kaluza i Oskar Klein explicava de manera unificada l'electromagnetisme i la gravetat, postulant un univers de 5 dimensions amb una dimensió compactificada (teoria Kaluza-Klein).
Exemples de formes tridimensionals

En geometria, són tridimensionals les següents figures geomètriques:[4]
- Poliedres de cares planes:
- Superfícies corbes:
Totes elles poden ser embegudes en un espai euclidià de tres dimensions. No obstant això, cal assenyalar que tècnicament l'esfera, el con o el cilindre són varietats bidimensionals (només la closca), ja que els punts interiors en aquestes figures no són estrictament part d'aquestes. Només per un abús de llenguatge o extensió d'aquest, informalment es parla d'esferes, cilindres o cons incloent-hi el seu interior.
A més, hi ha la hiperesfera tridimensional (3-varietat), però no és la pela d'una bola sinó la compactificació de amb un punt, així com la 2-esfera és per al pla euclidià .
Sistemes tridimensionals en ciències naturals
En química, es parla de sistemes tridimensionals quan l'enllaç químic és igualment intens en les tres direccions de l'espai (per exemple, en el diamant). En magnetisme, es diu que l'ordenament magnètic només és possible si l'acoblament magnètic és tridimensional (és a dir, s'estén en les tres direccions de l'espai). En matemàtiques, el sistema tridimensional es representa en el pla cartesià amb els eixos X, Y i Z. En general, en aquestes representacions s'utilitzen les formes geomètriques de tres dimensions com els cubs o les esferes.
Simulació 3D
Avui dia, és possible la simulació mitjançant càlculs basats en la projecció d'entorns tridimensionals sobre pantalles bidimensionals, com ara monitors d'ordinador o televisors. Aquests càlculs requereixen una gran càrrega de procés, per la qual cosa alguns ordinadors i consoles disposen d'un cert grau d'acceleració gràfica 3D gràcies a dispositius desenvolupats per a tal fi. Els ordinadors disposen de les anomenades targetes gràfiques amb acceleració 3D. Aquests dispositius estan formats amb un o diversos processadors (GPU), dissenyats especialment per accelerar els càlculs que suposen reproduir imatges tridimensionals sobre una pantalla bidimensional i d'aquesta forma alliberar de càrrega de procés la CPU o unitat de procés central de l'ordinador.
Geometria
Polítops
En tres dimensions, hi ha nou polítops regulars: cinc de convexos i quatre de no convexos. Els convexos són els sòlids platònics, mentre que els no convexos són els poliedres de Kepler-Poinsot.
- Petit dodecaedre estrellat
- Gran dodecaedre estrellat
Superfícies quàdriques
En analogia amb les seccions còniques, el conjunt de punts les coordenades cartesianes dels quals satisfan l'equació general de segon ordre, és a dir,
on A, B, C, F, G, H, J, K, L i M són nombres reals i no tots els termes A, B, C, F, G i H valen zero, rep el nom de superfície quàdrica.[5]
Hi ha sis tipus de superfícies quàdriques no degenerades:
- L'el·lipsoide
- L'hiperboloide d'una cara
- L'hiperboloide de dues cares
- El con el·líptic
- El paraboloide el·líptic
- El paraboloide hiperbòlic
Les superfícies quàdriques degenerades són el conjunt buit, el punt, la línia recta, el pla, una parella de plans o un cilindre quadràtic (una superfície que consisteix a una secció cònica no degenerada en un pla i totes les línies de R3 a través d'aquella cònica que són normals a ).[5] De vegades també es consideren els cons el·líptics com superfícies quàdriques degenerades.
Tant l'hiperboloide d'una cara com el paraboloide hiperbòlic són superfícies reglades, en el sentit que es poden construir a partir d'una família de línies rectes. De fet, cadascun d'ells té dues famílies de línies generadors, els memebre de cada família són disjunts i cada membre d'una família creua cada membre de l'altra família, amb només una excepció.[6] Cada família rep el nom de regulus.
En topologia

L'espai tridimensional té un seguit de propietats topològiques que el diferencien d'espais de dimensió diferent. Per exemple, calen un mínim de tres dimensions per lligar un nus en un tros de corda.[7]
En geometria diferencial els espais tridimensionals genèrics són les 3-varietats, que localment semblen .
En càlcul
Gradient, divergència i rotacional
En un sistema de coordenades rectangular, el gradient d'una funció (diferenciable) ve donat per
que, en notació d'índex, s'escriu
La divergència d'un camp vectorial (diferenciable) F = U i + V j + W k, és a dir una funció , és igual a la funció escalar:
En notació d'índex, seguint la notació d'Einstein, s'escriu
Expandit en coordenades cartesianes (vegi's operador nabla en coordenades cilíndriques i esfèriques per representacions en coordenades esfèriques i cilíndriques), el rotacional ∇ × F és, per F compost per [Fx, Fy, Fz]:
on i, j, i k són els vectors unitaris pels eixos x, y, i z, respectivament. El rotacional s'expandeix com:[8]
En notació d'índex, amb el conveni d'Einstein és
on és el símbol totalment antisimètric, el símbol de Levi-Civita.
Integrals de línia de superfície i de volum
Donat un camp escalar f : U ⊆ Rn → R, la integral de línia al llarg d'una corba suau a trossos C ⊂ U és definida com
on r: [a, b] → C és una parametrització bijectiva arbitrària de la corba C tal que r(a) i r(b) donen els punts extrems de C i .
Donat un camp vectorial F : U ⊆ Rn → Rn, la integral de línia al llarg d'una corba suau a trossos C ⊂ U, en la direcció de r, és definida com
on · és el producte escalar i r: [a, b] → C és una parametrització bijectiva de la corba C tal que r(a) i r(b) donen els punts finals de C.
Una integral de superfície és una generalització de les integrals múltiples a la integració sobre superfícies. Es pot entendre com l'anàleg d'una integral doble a la integral de línia. Per trobar una fórmula explícita per la integral de superfície, cal parametritzar la superfície d'interès, S, considerant un sistema de coordenades curvilínies en S, com ho són la latitud i longitud en una esfera. Sigui tal parametrització x(s, t), on (s, t) varien dins una certa regió T en el pla. Llavors, la integral de superfície ve donada per
on l'expressió entre barres a la banda dreta de la igualtat és la magnitud del producte vectorial de les derivades parcials de x(s, t), i es coneix com l'element superfície. Donat un camp vectorial v en S, és a dir una funció que assigna a cada x en S un vector v(x), es pot definir la integral de superfície component per component segons la definició de la integral de superfície d'un camp escalar; el resultat és un vector.
Una integral de volum és una integral sobre un domini o regió tridimensional. Quan l'integrand és trivial (la unitat), la integral de volum és simplement el volum de la regió.[9][10] També pot voler dir una integral triple en una regió D de R3 d'una funció i sovint s'escriu:
Teorema fonamental de les integrals de línia
El teorema fonamental de les integrals de línia afirma que es pot avaluar una integral de línia a través d'un camp que és el gradient d'un camp escalar simplement calculant el valor del camp escalar en els punts finals de la corba.
Sigui . Llavors
Teorema de Stokes
El teorema de Stokes relaciona la integral de superfície del rotacional d'un camp vectorial F en una superfície Σ de l'espai euclidià tridimensional amb la integral de línia del camp vectorial avaluat en la seva frontera ∂Σ:
Teorema de la divergència
Sigui V un subconjunt de (en el cas de n = 3, V representa un volum en l'espai tridimensional) que és compacte i té una frontera suau a trossos S (també indicat com ∂V = S). Si F és un camp vectorial contínuament diferenciable definit en un veïnat de V, llavors el teorema de la divergència de Gauss afirma que:[11]
El costat esquerre de la igualtat és la integral de volum en el volum V, el costat dret és la integral de superfície en la frontera del volum V. La varietat tancada ∂V és de forma bastant general la frontera de V orientada per les normals de la superfície apuntant cap a fora, i és el camp de la normal unitària de la frontera ∂V apuntant cap a fora. (Es pot utilitzar dS com a abreviatura de ndS.)
Referències
Vegeu també
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.









































![{\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p} ,\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b27cdd0377931a70cbb0635e37781a42e7fe33f9)