Cub

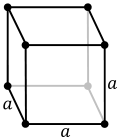
Un cub, hexàedre regular o hexaedre regular és un políedre regular format per sis cares quadrades en el qual en cada vèrtex hi coincideixen tres arestes perpendiculars entre si. El seu volum es calcula segons la fórmula a³, on a és la longitud d'una aresta.^[1]

Cub

Model 3D
Tipus	sòlid platònic, hipercub, zonoedre, trapezoedre trigonal, romboedre, ortoedre, prisma quadrilateral, objecte 3D i hexàedre
Forma de les cares	quadrat (6)
Configuració de vèrtex	triangle equilàter
Símbol de Schläfli	{4,3}
Dual	octàedre regular
Elements
Vèrtexs	8
Arestes	12
Cares	6
Més informació
MathWorld	Cube

Una diagonal de cara es denota com ${\displaystyle AC}$ i una diagonal espacial és ${\displaystyle AC'}$

El cub és l'únic hexàedre regular i forma part dels cinc sòlids platònics. Té 6 cares, 8 vèrtexs i 12 arestes. També és un paral·lelepípede quadrat i un cuboide equilateral. És un prisma quadrat regular en tres orientacions i un trapezoedre trigonal en quatre orientacions. És el dual de l'octàedre i té simetria octaèdrica o cúbica. Finalment, és l'únic políedre convex que té totes les cares quadrades.

Propietats

Un cub és un políedre amb vuit vèrtexs i dotze arestes de la mateixa longitud, que formen sis quadrats com a cares. Un cub és un cas especial d'un ortoedre rectangular, que té sis cares rectangulars, cadascuna de les quals té un parell d'arestes oposades de la mateixa longitud i paral·leles.^[2] Tots dos políedres tenen el mateix angle diedre, l'angle entre dues cares adjacents en una aresta comuna, un angle recte o 90°, obtingut a partir de l'angle interior (un angle format entre dos costats adjacents en un punt comú d'un polígon dins) d'un quadrat.^[3][4] Més generalment, el cub i l'ortoedre rectangular són casos especials d'un ortoedre, un políedre amb sis quadrilàters (un polígon de quatre costats).^[5] Com per a tots els políedres convexos, el cub té una característica d'Euler de 2, segons la fórmula ${\displaystyle V-E+F=2}$ ; les tres lletres denoten respectivament el nombre de vèrtexs, arestes i cares.^[6]

Les tres cares quadrades que envolten un vèrtex són ortogonals entre si, és a dir, els plans són perpendiculars, formant un angle recte entre dos quadrats adjacents. Per tant, el cub es classifica com a políedre ortogonal.^[7] El cub és un cas especial d'altres quadrats. Aquests inclouen un paral·lelepípede, un políedre amb sis cares de paral·lelograms, perquè els seus parells de cares oposades són congruents;^[8] un romboedre, com a cas especial d'un paral·lelepípede amb sis cares de rombes, perquè l'angle interior de totes les cares és recte;^[9] i un trapezoedre trigonal, un políedre amb cares quadrilàteres congruents, ja que les seves cares quadrades són els casos especials dels rombes.^[10]

El cub és un políedre elemental o no compost. És a dir, cap pla que intersequi la seva superfície només al llarg de les arestes, tallant així en dos o més políedres convexos de cares regulars.^[11]

Mesura i altres propietats mètriques

Donat un cub amb una longitud d'aresta ${\displaystyle a}$, la diagonal de la cara del cub és la diagonal d'un quadrat ${\displaystyle a{\sqrt {2}}}$, i la diagonal espacial del cub és una línia que connecta dos vèrtexs que no es troben a la mateixa cara, formulada com ${\displaystyle a{\sqrt {3}}}$. Ambdues fórmules es poden determinar mitjançant el teorema de Pitàgores ${\displaystyle a{\sqrt {3}}}$. L'àrea de la superfície d'un cub ${\displaystyle A}$ és sis vegades l'àrea d'un quadrat:^[12] $${\displaystyle A=6a^{2}.}$$ El volum d'un ortoedre és el producte de la seva longitud, amplada i alçada. Com que totes les arestes d'un cub tenen la mateixa longitud, la fórmula per al volum d'un cub és la tercera potència de la longitud del seu costat.^[12] Això porta a l'ús del terme cub com a verb, per significar elevar qualsevol nombre a la tercera potència:^[5] $${\displaystyle V=a^{3}.}$$Un cas especial és el cub unitari, anomenat així per mesurar una sola unitat de longitud al llarg de cada aresta. D'això es dedueix que cada cara és un quadrat unitari i que la figura sencera té un volum d'1 unitat cúbica.^[13][14] El príncep Rupert del Rin, conegut per la gota del príncep Rupert, va qüestionar si un cub podia passar a través d'un forat tallat al cub unitari. La resposta és que el cub pot passar a través d'una còpia de si mateix de la mateixa mida o més petita.^[15][16] Les seves arestes són un 6% més llargues que el cub unitari, obtingut pel teorema de Pitàgores o equivalentment la fórmula de la distància euclidiana en un espai tridimensional.^[17] Un antic problema de duplicar el cub també conegut com el problema de Delos requereix la construcció d'un cub amb un volum el doble de l'original utilitzant només un compàs i un regle. Això va ser conclòs pel matemàtic francès Pierre Wantzel el 1837, demostrant que és impossible d'implementar, ja que un cub amb el doble de volum de l'original l'arrel cúbica de 2, ${\displaystyle {\sqrt[{3}]{2}}}$ no és construïble.^[18] Tanmateix, Messer (1986) va resoldre aquest problema plegant un paper d'origami.^[19]

El cub del Príncep Rupert

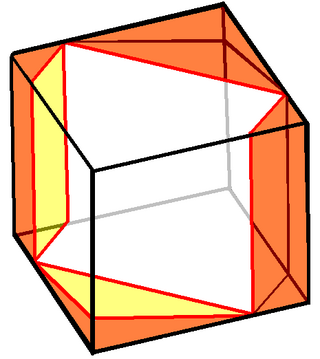
El cub té tres tipus de geodèsiques tancades, o camins a la superfície d'un cub que són localment rectes. En altres paraules, eviten els vèrtexs, segueixen segments de línia a través de les cares que creuen i formen angles complementaris a les dues cares incidents de cada aresta que creuen. Un tipus es troba en un pla paral·lel a qualsevol cara del cub, formant un quadrat congruent a una cara, quatre vegades la longitud de cada aresta. Un altre tipus es troba en un pla perpendicular a la diagonal llarga, formant un hexàgon regular; la seva longitud és ${\displaystyle 3{\sqrt {2}}}$ vegades la d'una aresta. El tercer tipus és un hexàgon no pla.^[20]

Insfera, midsfera, circumsfera

Una esfera interior d'un cub ${\displaystyle r_{i}}$ és una esfera tangent a les cares d'un cub en els seus centroides. La seva meitat esfera ${\displaystyle r_{m}}$ és una esfera tangent a les arestes d'un cub. La seva circumsfera ${\displaystyle r_{c}}$ és una esfera tangent als vèrtexs d'un cub. Amb longitud d'aresta ${\displaystyle a}$, són respectivament:^[21] $${\displaystyle r_{i}={\frac {1}{2}}a=0.5a,\qquad r_{m}={\frac {\sqrt {2}}{2}}a\approx 0.707a,\qquad r_{c}={\frac {\sqrt {3}}{2}}a\approx 0.866a.}$$

Simetria

El poliedre dual d'un cub és l'octaedre regular. Tots dos tenen simetria octaèdrica.

Un hexaedre regular (o cub) té quinze eixos de simetria d'ordre quatre: les rectes perpendiculars a cada parell de cares paral·leles pel seu punt mitjà; quatre eixos de simetria d'ordre dos: les rectes que uneixen els centres d'arestes oposades; nou plans de simetria; tres paral·lels a cada parell de cares paral·leles pel punt mitjà de les arestes que les uneixen, i sis formats pels parells d'arestes oposades; i un centre de simetria. Això fa que aquest cos tingui un ordre de simetria total de 48: 2x(3x4+6x2).

Els elements de simetria anteriors defineixen un dels grups de simetria octaèdrics, el denominat O_h segons notació de Schöenflies.

El cub té simetria octaèdrica ${\displaystyle \mathrm {O} _{\mathrm {h} }}$ d'ordre 48. En altres paraules, el cub té 48 isometries (inclosa la identitat), cadascuna de les quals transforma el cub en si mateix. Aquestes transformacions inclouen nou simetries de reflexió (on dues meitats tallades per un pla són idèntiques): tres tallen el cub als punts mitjans de les seves arestes i sis tallen en diagonal. El cub també té tretze eixos de simetria rotacional (on la rotació al voltant de l'eix dona com a resultat una aparença idèntica): tres eixos passen pels centroides de les cares oposades, sis pels punts mitjans de les arestes oposades i quatre pels vèrtexs oposats; aquests eixos són respectivament simetria rotacional quàdruple (0°, 90°, 180° i 270°), simetria rotacional doble (0° i 180°) i simetria rotacional triple (0°, 120° i 240°).^{[22][23][24][25]}

El políedre dual es pot obtenir a partir de cadascun dels vèrtexs dels políedres tangents a un pla mitjançant un procés conegut com a reciprocació polar.^[26] Una propietat dels políedres duals és que el políedre i el seu dual comparteixen el seu grup de punts de simetria tridimensional. En aquest cas, el políedre dual d'un cub és l'octaedre regular, i tots dos políedres tenen la mateixa simetria octaèdrica.^[27]

El cub és transitiu de cares, és a dir, que les seves dues cares quadrades són iguals i es poden representar per rotació i reflexió.^[28] És transitiu de vèrtexs, és a dir, que tots els seus vèrtexs són equivalents i es poden representar isomètricament sota la seva simetria.^[29] També és transitiu d'arestes, és a dir, que el mateix tipus de cares envolten cadascun dels seus vèrtexs en el mateix ordre o en ordre invers, i cada parell de cares adjacents té el mateix angle diedre. Per tant, el cub és un políedre regular.^[30] Cada vèrtex està envoltat per tres quadrats, de manera que el cub és ${\displaystyle 4.4.4}$ per configuració de vèrtex o ${\displaystyle \{4,3\}}$ pel símbol de Schläfli.^[31]

Geometria i fórmules

Donat un cub regular d'aresta ${\displaystyle a}$:

Àrea de la superfície	${\displaystyle 6a^{2}\,}$	Volum	${\displaystyle a^{3}\,}$
Diagonal facial	${\displaystyle {\sqrt {2}}a}$	Diagonal espacial	${\textstyle {\sqrt {3}}a}$
Radi de l'esfera circumscrita	${\displaystyle {\frac {\sqrt {3}}{2}}a}$	Radi de l'esfera tangent a les arestes	${\displaystyle {\frac {a}{\sqrt {2}}}}$
Radi de l'esfera inscrita	${\displaystyle {\frac {a}{2}}}$	Angles entre cares (en radians)	${\displaystyle {\frac {\pi }{2}}}$

Com que el volum del cub és la potència tercera de les seves arestes (${\displaystyle a\times a\times a}$), les potències terceres s'anomenen «cub» per analogia a «quadrat» i les potències segones.

El cub té el volum més gros entre tots els cuboides amb una mateixa àrea superficial. A més a més, el cub també té el volum més gros entre els cuboides amb la mateixa longitud d'aresta total (amplada + llargada + alçada).

Punt en l'espai

Per un cub l'esfera circumscrita del qual tingui radi R, i per un punt donat del seu espai tridimensional amb distàncies d_i respecte els vuit vèrtexs del cub, s'obté:^[32]

${\displaystyle {\frac {\sum _{i=1}^{8}d_{i}^{4}}{8}}+{\frac {16R^{4}}{9}}=\left({\frac {\sum _{i=1}^{8}d_{i}^{2}}{8}}+{\frac {2R^{2}}{3}}\right)^{2}.}$

Coordenades cartesianes i equació en l'espai tridimensional

Coordenades cartesianes

Per un cub centrat en l'origen, amb arestes paral·leles als eixos i amb una longitud d'aresta de 2, les coordenades cartesianes dels vèrtexs són:

(±1, ±1, ±1)

Mentre que l'interior consisteix en tots els punts (x₀, x₁, x₂) amb −1 < x_i < 1 per tot i.

Equació en l'espai tridimensional

En geometria analítica, la superfície d'un cub amb centre (x₀, y₀, z₀) i llargada d'aresta 2a és el locus de tots els punts (x, y, z) tals que

${\displaystyle \max\{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|\}=a.}$

Projeccions ortogonals

El cub té quatre projeccions ortogonals especials: centrada en un vèrtex, aresta o cara, i normal a la seva figura de vèrtex. La primera i tercera corresponen als plans de Coxeter A₂ and B₂.

Projeccions ortogonals

Centratge per	Cara	Vèrtex
Plans de Coxeter	B₂	A₂
Simetria projectiva	[4]	[6]
Vistes laterals

Políedre esfèric

El cub també es pot representar com un políedre esfèric i ser projectat sobre el pla per mitjà d'una projecció estereogràfica. Aquesta projecció és conforme, és a dir, preserva els angles però no pas les àrees o llargades. Les línies rectes de l'esfera es projecten com a arcs circulars sobre el pla.

Projecció ortogràfica	Projecció estereogràfica

En la cultura

Un dau de sis cares

Un Skewb completat

L'Escultura de l'Alamo

Els cubs han aparegut en molts papers en la cultura popular. És la forma més comuna de daus.^[28] Joguines de trencaclosques com ara peces d'un cub Soma,^[33] el cub de Rubik i Skewb estan construïts amb cubs.^[34] Minecraft és un exemple d'un videojoc de tipus sandbox de blocs cúbics.^[35] L'escultura a l'aire lliure Alamo (1967) és un cub que gira al voltant del seu eix vertical.^[36] Il·lusions òptiques com el cub impossible i el cub de Necker han estat explorades per artistes com MC Escher.^[37] El cub es va aplicar al tractat d' Alberti sobre arquitectura renaixentista, De re aedificatoria (1450).^[38] Les cases cúbiques als Països Baixos són un conjunt de cases cúbiques les diagonals hexagonals de les quals es converteixen en la planta principal.^[39]

Des d'anys passats, i en nombroses cultures, el cub és la forma més utilitzada per donar forma als daus, utilitzats en molts llocs. En els jocs de rol l'anotació escrita en el dau de sis cares és «D6».

En teologia, els cubs apareixen a les religions abrahàmiques. La Kaaba de la Meca n'és un exemple, ja que significa justament «cub» en àrab. També apareixen al judaisme: teffilin i Nova Jerusalem al Nou Testament són descrits com a cubs.^[40]

El cub representa simbòlicament la veritat. I s'associava amb Hermes.^[41]

Estructura cristal·lina cúbica simple

Sal de taula cristalls cúbics

Model de bola i pal de cuban

Model sòlid platònic del sistema solar de Kepler

En la natura i la ciència

Els cubs també es troben en diversos camps de les ciències naturals i la tecnologia. S'aplica a la cel·la unitària d'un cristall conegut com a sistema cristal·lí cúbic.^[42] La sal de taula és un exemple d'un mineral amb una forma comunament cúbica.^[43] Altres exemples són la pirita (tot i que hi ha moltes variacions)^[9] i l'urani en forma cúbica en el programa nuclear.^[44] El radiolari Lithocubus geometricus, descobert per Ernst Haeckel, té una forma cúbica.^[45] El cuban és un hidrocarbur sintètic que consta de vuit àtoms de carboni disposats a les cantonades d'un cub, amb un àtom d'hidrogen unit a cada àtom de carboni.^[46]

Un intent històric d'unificar tres idees físiques de la relativitat, la gravitació i la mecànica quàntica va utilitzar el marc d'un cub conegut com a cub cGh.^[47] Els cubs tecnològics inclouen el dispositiu espacial CubeSat,^[48] el dispositiu de demostració de radiació tèrmica Leslie^[49] i la màquina servidora web Cobalt Qube.^[50] Les quadrícules cúbiques són habituals en els sistemes de coordenades cartesianes tridimensionals.^[51] En gràfics per ordinador, un algoritme divideix el volum d'entrada en un conjunt discret de cubs conegut com la unitat de la isosuperfície,^[52] i les cares d'un cub es poden utilitzar per mapejar una forma.^[53]

A l'antiguitat

Els sòlids platònics són cinc políedres coneguts des de l'antiguitat. El conjunt rep el nom de Plató, que va atribuir aquests sòlids a la natura en el seu diàleg Timeu. Un d'ells, el cub, representava l'element clàssic de la Terra a causa dels blocs de construcció dels fonaments de la Terra.^[54] Els Elements d'Euclides van definir els sòlids platònics, inclòs el cub, i van mostrar com trobar la relació entre el diàmetre de l'esfera circumscrita i la longitud de l'aresta.^[55]

Seguint l'ús que Plató feia dels políedres regulars com a símbols de la natura, Johannes Kepler, a la seva obra Harmonices Mundi, va esbossar cadascun dels sòlids platònics; va decorar el costat del cub amb un arbre.^[56] Al seu Mysterium Cosmographicum, Kepler va proposar l'estructura del sistema solar i les relacions entre els seus planetes extraterrestres amb el conjunt de sòlids platònics, inscrits i circumscrits per orbes esfèriques. Cada sòlid encapsulat en una esfera, dins de l'altra, produiria sis capes, corresponents als sis planetes coneguts: Mercuri, Venus, Terra, Mart, Júpiter i Saturn . De l'interior al exterior, aquests sòlids es van ordenar a partir de l'octaedre, seguit de l'icosaedre, el dodecaedre, el tetraedre i, finalment, el cub.^[57]

Construccions

Les onze xarxes d'un cub

El cub té onze xarxes diferents, que consisteixen en una disposició de quadrats units per les vores. Aquests quadrats es poden plegar al llarg de les vores i connectar-se a aquests polígons, que finalment es converteixen en les cares d'un cub.^[58][59]

En geometria analítica, un cub es pot construir utilitzant els sistemes de coordenades cartesianes . Per a un cub centrat a l'origen, amb arestes paral·leles als eixos i amb una longitud d'aresta de 2, les coordenades cartesianes dels vèrtexs són ${\displaystyle (\pm 1,\pm 1,\pm 1)}$^[60] El seu interior està format per tots els punts ${\displaystyle (x_{0},x_{1},x_{2})}$ amb ${\displaystyle -1<x_{i}<1}$ per a tots ${\displaystyle i}$ La superfície d'un cub amb centre ${\displaystyle (x_{0},y_{0},z_{0})}$ i la longitud de la vora de ${\displaystyle 2a}$ és el lloc geomètric de tots els punts ${\displaystyle (x,y,z)}$ de tal manera que $${\displaystyle \max\{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|\}=a.}$$El cub és un polítop de Hanner, perquè es pot construir utilitzant el producte cartesià de tres segments de línia. El seu políedre dual, l'octaedre regular, es construeix mitjançant la suma directa de tres segments de línia.^[61]

El gràfic d'un cub

Representació

Com a gràfic

Segons el teorema de Steinitz, un graf es pot representar com el graf vèrtex-aresta d'un poliedre. Aquest graf té dues propietats: planar (les arestes d'un graf estan connectades a cada vèrtex sense creuar altres arestes) i 3-connex (sempre que un graf amb més de tres vèrtexs, i dos dels vèrtexs s'eliminen, les arestes romanen connectades).^[62][63] L'esquelet d'un cub, representat com el graf, s'anomena graf cúbic, un graf platònic. Té el mateix nombre de vèrtexs i arestes que el cub, dotze vèrtexs i vuit arestes.^[64] El graf cúbic també es classifica com a graf de prisma, que s'assembla a l'esquelet d'un ortoedre.^[65]

El graf cúbic és un cas especial de graf hipercub o ${\displaystyle n}$- cub — denotat com ${\displaystyle Q_{n}}$ — perquè es pot construir utilitzant el producte cartesià de gràfics: dos gràfics que connecten el parell de vèrtexs amb una aresta per formar un nou gràfic.^[66] En el cas del gràfic cúbic, és el producte de ${\displaystyle Q_{2}\mathbin {\Box } Q_{1}}$, on ${\displaystyle \mathbin {\Box } }$ denota el producte cartesià de gràfics. En altres paraules, el gràfic cúbic es construeix connectant cada vèrtex de dos quadrats amb una aresta. Notacionalment, el gràfic cúbic és ${\displaystyle Q_{3}}$^[67] Com qualsevol gràfic d'hipercub, té un cicle que visita cada vèrtex exactament una vegada,^[68] i també és un exemple de gràfic de distància unitària.^[69]

El graf cúbic és bipartit, és a dir, cada conjunt independent de quatre vèrtexs pot ser disjunt i les arestes connectades en aquests conjunts.^[70] Tanmateix, cada vèrtex d'un conjunt no pot connectar tots els vèrtexs del segon, de manera que aquest graf bipartit no és complet.^[71] És un exemple tant d'un graf corona com d'un graf Kneser bipartit.^[72][70]

En projecció ortogonal

Un objecte il·luminat per raigs de llum paral·lels projecta una ombra sobre un pla perpendicular a aquests raigs, anomenat projecció ortogonal. Un poliedre es considera equipojectiu si, per a alguna posició de la llum, la seva projecció ortogonal és un polígon regular. El cub és equipojectiu perquè, si la llum és paral·lela a una de les quatre línies que uneixen un vèrtex amb el vèrtex oposat, la seva projecció és un hexàgon regular.^[73]

Com a matriu de configuració

El cub es pot representar com una matriu de configuració, una matriu en què les files i columnes corresponen als elements d'un poliedre com els vèrtexs, les arestes i les cares. La diagonal d'una matriu denota el nombre de cada element que apareix en un poliedre, mentre que la no diagonal d'una matriu denota el nombre d'elements de la columna que es produeixen a l'element de la fila o a l'element. Els vuit vèrtexs, les dotze arestes i les sis cares del cub es denoten per cada element de la diagonal d'una matriu (8, 12 i 6). La primera columna de la fila del mig indica que hi ha dos vèrtexs a cada aresta, denotats com a 2; la columna del mig de la primera fila indica que tres arestes es troben a cada vèrtex, denotades com a 3. La matriu de configuració d'un cub és:^[74] $${\displaystyle {\begin{bmatrix}{\begin{matrix}8&3&3\\2&12&2\\4&4&6\end{matrix}}\end{bmatrix}}}$$

Figures relacionades

Alguns dels políedres construïts a partir d'un cub: l'octaedre estrellat, el hexaedre tetrakis i el cub bisellat

Construcció de políedres

Es poden construir molts políedres a partir d'un cub. Alguns exemples són:

• Quan es faceta un cub, és a dir, eliminar part de les cares poligonals sense crear nous vèrtexs d'un cub, el poliedre resultant és l'octaedre estrellat.^[75]
• Es poden construir nous políedres convexos unint políedres menys regulars a les cares d'un cub.^[11] El cub és, doncs, un component de dos sòlids de Johnson, la piràmide quadrada allargada i la bipiràmide quadrada allargada, aquesta última sent un cub amb piràmides quadrades a les cares oposades.^[76]
• Si s'uneix una piràmide baixa a cada cara d'un cub, es produeix el seu kleetope, el tetrakishexaedre,^[77] dual de l'octaedre truncat.

• La subdivisió baricèntrica d'un cub (o del seu dual, l'octaedre regular) és el dodecaedre disdyakis, un sòlid català.^[78]
• La regió de la cantonada d'un cub també es pot truncar per un pla (per exemple, coberta pels tres vèrtexs veïns), donant com a resultat un tetraedre trirectangular.^[79]
• El cub snub és un sòlid arquimediano que es pot construir separant les cares del cub i omplint els buits amb triangles equilàters amb angles retorçats, un procés conegut com a snub.^[80]
• Cadascun dels vèrtexs del cub es pot truncar, i el políedre resultant és el sòlid d'Arquimedes, el cub truncat.^[56] Quan les seves arestes estan truncades, és un rombicuboctaedre.^[81]
• De la mateixa manera, el rombicuboctaedre també es pot construir separant les cares del cub i després expandint-les, després afegint altres cares triangulars i quadrades entre elles; això es coneix com a "cub expandit". La mateixa figura es pot derivar de la mateixa manera a partir del dual del cub, l'octaedre regular.^[82]

• El cub bisellat es construeix a partir d'un cub mitjançant un operador truncant anomenat xamfrà . El poliedre resultant té dotze cares hexagonals i sis quadrades amb simetria central, un zonoedre.^[83][84]
• Es poden construir tres rectangles àuris mútuament perpendiculars a partir d'un parell de vèrtexs situats als punts mitjans de les arestes oposades de la superfície d'un cub, dibuixant una línia de segment entre aquests dos i dividint aquesta línia de segment en una proporció àuria des del seu punt mitjà. Les cantonades d'aquests rectangles són els vèrtexs d'un icosaedre regular amb vint triangles equilàters.^[56]

El cub es pot construir amb sis piràmides quadrades, tessel·lant l'espai unint els seus vèrtexs. En alguns casos, això produeix el dodecàedre ròmbic que circumscriu un cub.^[85][86]

Policubs

Dos exemples de policubs són un policub amb cinc cubs units cara a cara i la creu de Dalí . Aquesta última és una de les 261 xarxes d'un tesseract.

Un policub és una figura sòlida formada unint un o més cubs iguals cara a cara. Els policubs són els anàlegs tridimensionals dels poliominòs bidimensionals.^[87]

Quan quatre cubs s'apilen verticalment i quatre més s'uneixen al segon cub de dalt de la pila, el policub resultant és la creu de Dalí, que rep el nom de l'artista surrealista espanyol Salvador Dalí, la pintura del qual Corpus Hypercubus (1954) conté un tesseract que es desplega en una creu de sis braços; una construcció similar és fonamental per al conte de Robert A. Heinlein "I va construir una casa torta" (1940).^[88][89] La creu de Dalí es pot plegar en una quarta dimensió per tancar un tesseract^[90] Un cub és una instància tridimensional d'un hipercub (també conegut com a 3-cub); l'hipercub bidimensional (2-cub) és un quadrat, i l'hipercub tetradimensional (4-cub) és un tesseract.^[91]

Omplint l'espai

El panal cúbic és un exemple de panal en l'espai tridimensional euclidià.

Un cub pot aconseguir un bresca omplint-lo juntament amb la seva còpia en un espai tridimensional sense deixar un buit. Els cubs són ompliments d'espai, on la frase "ompliment d'espai" es pot entendre com una tessel·lació generalitzada.^[92] El cub és un plesiòedre, un tipus especial de políedre que omple l'espai que es pot definir com la cel·la de Voronoi d'un conjunt de Delone simètric.^[93] Els plesiòedres inclouen els paral·leloedres, que es poden traduir sense girar per omplir un espai en què cada cara de qualsevol de les seves còpies està unida a una cara similar d'una altra còpia. Hi ha cinc tipus de paral·leloedres, un dels quals és el paral·lelepípede.^[94] Cada paral·leloedre tridimensional és un zonoedre, un políedre centralment simètric les cares del qual són polígons centralment simètrics.^[95]

Un exemple de bresca amb només un tipus cúbic, anomenat cel·la, és una bresca cúbica que consta de quatre cubs al voltant de les seves vores en un espai tridimensional euclidià.^[96] Més exemples en un espai tridimensional no euclidià són la bresca amb tres cubs al voltant de les seves vores en una esfera tridimensional i la bresca amb cinc cubs al voltant de les seves vores en un espai hiperbòlic.^[97] Qualsevol paral·lelepípede, inclòs un cub, pot aconseguir un panal si el seu invariant de Dehn és zero.^[98] L'inici de l'invariant de Dehn es remunta al tercer problema de Hilbert, si dos políedres de volum igual es poden disseccionar sempre en peces polièdriques i tornar a muntar-se entre si. Si és així, aleshores el volum de qualsevol políedre es podria definir axiomàticament com el volum d'un cub equivalent en el qual es podria tornar a muntar. Aquest problema va ser resolt per Max Dehn, inventant el seu invariant, responent que no tots els políedres es poden tornar a muntar en un cub.^[99] Va demostrar que dos políedres de volum igual haurien de tenir el mateix invariant de Dehn, excepte els dos tetràedres els invariants de Dehn dels quals eren diferents.^[100]

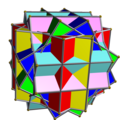
Enumeració segons Skilling (1976): compost de sis cubs amb llibertat de rotació ${\displaystyle \mathrm {UC} _{7}}$, tres cubs ${\displaystyle \mathrm {UC} _{8}}$, i cinc cubs ${\displaystyle \mathrm {UC} _{9}}$

Diversos

Cub esfèric

Una vista en torus tridimensional

Els compostos polièdrics, en què els cubs comparteixen el mateix centre, són compostos polièdrics uniformes, és a dir, que són compostos polièdrics els constituents dels quals són idèntics — que possiblement enantiomorfs— en una disposició que també és uniforme. Respectivament, la llista de compostos enumerats per Skilling (1976) del setè al novè compost uniforme per al compost de sis cubs amb llibertat de rotació, tres cubs i cinc cubs.^[101] Dos compostos, que consten de dos i tres cubs, es van trobar a la xilografia d'Escher Stars i al llibre de Max Brückner Vielecke und Vielflache.^[102]

El cub esfèric representa el poliedre esfèric, que es pot modelar amb els arcs de cercles màxims, creant límits com les arestes d'un quadrat esfèric.^[103] Per tant, el cub esfèric consta de sis quadrats esfèrics amb angles interiors de 120° a cada vèrtex. Té equilibri vectorial, és a dir, que la distància des del centroide i cada vèrtex és la mateixa que la distància des d'aquest fins a cada aresta.^[104][105] El seu dual és l'octaedre esfèric.^[103]

L'objecte topològic tor tridimensional és un espai topològic definit com a homeomorf al producte cartesià de tres cercles. Es pot representar com un model tridimensional de la forma del cub.^[106]