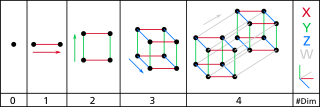Tesseractis

En geometria, un tesseractis^[1] o 4-cub és un hipercub de quatre dimensions, anàleg a un quadrat bidimensional i a un cub tridimensional.^[2] De la mateixa manera que el perímetre del quadrat consta de quatre arestes i la superfície del cub consta de sis cares quadrades, la hipersuperfície del tesseractis consta de vuit cel·les cúbiques, que es troben en angle recte. El tesseractis és un dels sis 4-polítops regulars convexos.^[3]

La creu de Dalí, una xarxa d'un tesseract

Tesseractis

Una projecció 3D d'una figura de 8 cel·les que realitza una rotació simple al voltant d'un pla que bisecciona la figura de davant a l'esquerra cap a darrere a la dreta i de dalt a baix. Creat per Jason Hise amb Maya i Macromedia Fireworks
Tipus	polícoron regular convex, hipercub, duoprisma i octàtop
Forma de les cares	cub (8)
Configuració de vèrtex	tetràedre
Símbol de Schläfli	{4,3,3}
Dual	16-cell (en)
Elements
Vèrtexs	16
Arestes	32
Cares	24
Cell	8
Més informació
MathWorld	Tesseract

El tesseractis també s'anomena octacoron de 8 cel·les, _C8, (regular) o prisma cúbic. És el polítop de mesura tetradimensional, pres com a unitat d'hipervolum.^[4] Coxeter l'anomena polítop γ₄ ^[5] El terme hipercub sense una referència de dimensió es tracta sovint com a sinònim d'aquest polítop específic.

L'Oxford English Dictionary fa que la paraula tesseract es derivi del llibre de Charles Howard Hinton de 1888 , *A New Era of Thought*. El terme deriva del grec téssara (τέσσαρα 'quatre') i aktís (ἀκτίς 'raig'), referint-se a les quatre arestes des de cada vèrtex fins als altres vèrtexs. Hinton originalment va escriure la paraula com a tessaract.^[6]

El tesseractis es pot desplegar en vuit cubs en un espai tridimensional, de la mateixa manera que el cub es pot desplegar en sis quadrats en un espai bidimensional.

Geometria

Com a polítop regular amb tres cubs plegats al voltant de cada aresta, té el símbol de Schläfli {4,3,3} amb simetria hiperoctaèdrica d'ordre 384. Construït com un hiperprisma 4D fet de dos cubs paral·lels, es pot anomenar símbol de Schläfli compost {4,3} × { }, amb ordre de simetria 96. Com a duoprisma 4-4, un producte cartesià de dos quadrats, es pot anomenar amb un símbol de Schläfli compost {4}×{4}, amb ordre de simetria 64. Com a ortotop es pot representar mitjançant el símbol compost de Schläfli { } × { } × { } × { } o { }⁴, amb ordre de simetria 16.

Com que cada vèrtex d'un tesseractis és adjacent a quatre arestes, la figura del vèrtex del tesseractis és un tetràedre regular. El polítop dual del tesseractis és el 16-cel·lular amb símbol de Schläfli {3,3,4}, amb el qual es pot combinar per formar el compost de tesseractis i 16-cel·lular.

Cada aresta d'un tesseractis regular té la mateixa longitud. Això és d'interès quan s'utilitzen tesseracts com a base d'una topologia de xarxa per enllaçar múltiples processadors en computació paral·lela : la distància entre dos nodes és com a màxim de 4 i hi ha molts camins diferents per permetre l'equilibri de pesos.

Un tesseractis està delimitat per vuit hiperplans tridimensionals. Cada parell d'hiperplans no paral·lels s'interseca per formar 24 cares quadrades. Tres cubs i tres quadrats es tallen a cada aresta. Hi ha quatre cubs, sis quadrats i quatre arestes que es troben a cada vèrtex. En total, un tesseractis consta de 8 cubs, 24 quadrats, 32 arestes i 16 vèrtexs.

Coordenades

Un tesseractis unitari té una longitud de costat 1 i es pren normalment com a unitat bàsica per a l'hipervolum en un espai de 4 dimensions. El tesseractis unitari en un sistema de coordenades cartesianes per a un espai de 4 dimensions té dos vèrtexs oposats a les coordenades [0, 0, 0, 0] i [1, 1, 1, 1], i altres vèrtexs amb coordenades a totes les combinacions possibles de 0 s i 1 s. És el producte cartesià de l'interval unitari tancat [0, 1] en cada eix.

De vegades, un tesseractis unitari està centrat a l'origen, de manera que les seves coordenades són les més simètriques ${\displaystyle {\bigl (}{\pm {\tfrac {1}{2}}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}}{\bigr )}.}$ Aquest és el producte cartesià de l'interval tancat ${\displaystyle {\bigl [}{-{\tfrac {1}{2}}},{\tfrac {1}{2}}{\bigr ]}}$ en cada eix.

Un altre tesseractis habitualment convenient és el producte cartesià de l'interval tancat [−1, 1] a cada eix, amb vèrtexs a les coordenades (±1, ±1, ±1, ±1). Aquest tesseractis té una longitud de costat de 2 i un hipervolum 2⁴ = 16.

Xarxa

El desplegament d'un polítop s'anomena xarxa. Hi ha 261 xarxes diferents del tesseract.^[7] Els desplegaments del tesseractis es poden comptar mapejant les xarxes a arbres aparellats (un arbre junt amb una coincidència perfecta en el seu complement).

Cadascuna de les 261 xarxes pot enrajolar espais de 3.

Construcció

Una animació del canvi de dimensions

La construcció d'hipercubs es pot imaginar de la següent manera:

• Unidimensional: Dos punts A i B es poden connectar per formar una recta, donant lloc a un nou segment AB.
• Bidimensional: Dos segments paral·lels AB i CD separats per una distància AB es poden connectar per formar un quadrat, amb els vèrtexs marcats com a ABCD.
• Tridimensional: Dos quadrats paral·lels ABCD i EFGH separats per una distància AB es poden connectar per formar un cub, amb les cantonades marcades com a ABCDEFGH.
• 4-dimensional: Dos cubs paral·lels ABCDEFGH i IJKLMNOP separats per una distància AB es poden connectar per convertir-se en un tesseract, amb les cantonades marcades com a ABCDEFGHIJKLMNOP. Tanmateix, aquest posicionament paral·lel de dos cubs de manera que els seus 8 parells de vèrtexs corresponents estiguin separats cadascun per una distància AB només es pot aconseguir en un espai de 4 o més dimensions.

Les 8 cel·les del tesseractis es poden considerar (de tres maneres diferents) com dos anells entrellaçats de quatre cubs.^[8]

El tesseractis es pot descompondre en 4-polítops més petits. És l'embolcall convex del compost de dos semidemòcrates (16-cel·les). També es pot triangular en simplex de 4 dimensions (cel·les irregulars de 5 punts) que comparteixen els seus vèrtexs amb el tesseract. Se sap que hi 92.487.256 triangulacions d'aquest tipus i que el nombre més baix de simplexis de 4 dimensions en qualsevol d'elles és de 16.

La dissecció del tesseractis en instàncies del seu simplex característic (un ortoesquema particular amb diagrama de Coxeter) ) és la construcció directa més bàsica possible del tesseract. La cel·la 5 característica del cub 4 és una regió fonamental del grup de simetria que defineix el tesseract, el grup que genera els polítops _B⁴. El simplex característic del tesseractis genera directament el tesseractis a través de les accions del grup, reflectint-se en les seves pròpies facetes delimitadores (les seves parets de mirall).^[9]