Rechtssystem (Mathematik)

Als Rechtssystem bzw. rechtshändiges Koordinatensystem werden in der Mathematik und in der Physik gewisse Systeme von zwei Vektoren in der Ebene bzw. drei Vektoren im Raum (mit einer festgelegten Reihenfolge) bezeichnet.

Achsenorientierung und Drehsinn linkshändiger und rechtshändiger Koordinatensysteme

Rechtssystem in der Ebene

Ein Rechtssystem in der Ebene sind zwei Vektoren ${\displaystyle {\vec {x}},{\vec {y}}}$, bei denen ${\displaystyle {\vec {y}}}$ aus ${\displaystyle {\vec {x}}}$ auf kürzestem Wege durch Drehung entgegen dem Uhrzeigersinn, d. h. im mathematisch positiven Drehsinn, hervorgeht.

Rechtssystem im Raum

Ein Rechtssystem im dreidimensionalen Raum sind drei Vektoren ${\displaystyle {\vec {x}},{\vec {y}}}$ und ${\displaystyle {\vec {z}}}$, wenn vom Endpunkt des Vektors ${\displaystyle {\vec {z}}}$ aus gesehen die Vektoren ${\displaystyle {\vec {x}},{\vec {y}}}$ ein Rechtssystem in der Ebene bilden.

Rechtssystem im ℝn

Ein Rechtssystem ist allgemein ein geordnetes Tupel ${\displaystyle ({\vec {x}}_{1},\dotsc ,{\vec {x}}_{n})}$ von Spaltenvektoren der Dimension ${\displaystyle n}$, sodass die Determinante der Matrix mit den Spaltenvektoren ${\displaystyle {\vec {x}}_{1},\dotsc ,{\vec {x}}_{n}}$ positiv ist.

Für ${\displaystyle n=2}$ und ${\displaystyle n=3}$ ist dies äquivalent zu obigen Definitionen.

Linkssysteme

Für Linkssysteme bzw. linkshändige Koordinatensysteme gilt jeweils das Umgekehrte. In der Ebene geht der zweite Vektor ${\displaystyle {\vec {y}}}$ durch Drehung im Uhrzeigersinn, d. h. mathematisch negativen Drehsinn, auf kürzestem Weg aus dem ersten Vektor ${\displaystyle {\vec {x}}}$ hervor, so wie er selbst seinerseits auf kürzestem Weg durch Drehung gegen den Uhrzeigersinn in den ersten Vektor überführt wird.^[1]

Ein Linkssystem in einem Vektorraum ist ein geordnetes Tupel von Spaltenvektoren, bei dem die dazugehörige Matrix eine negative Determinante hat. Dementsprechend ist ein Linkssystem im dreidimensionalen Raum ein geordnetes Tripel von Vektoren, für die das obige Spatprodukt negativ ist.

Regeln

Ob drei Vektoren ein Rechts- oder Linkssystem bilden, lässt sich mit Hilfe folgender Regeln bestimmen:^[2]

• Mit der Drei-Finger-Regel der rechten Hand (auch Rechte-Hand-Regel): Zeigt der abgespreizte Daumen in Richtung des ersten Vektors und der ausgestreckte Zeigefinger in Richtung des zweiten Vektors, zeigt der rechtwinklig zu Daumen und Zeigefinger abgespreizte Mittelfinger bei einem Rechtssystem in Richtung des dritten Vektors (das funktioniert auch bei zyklischer Vertauschung der Finger oder Vektoren: ${\displaystyle x-y-z,y-z-x,z-x-y}$).
• Mit der Schrauben- oder Korkenzieherregel: Wird der erste Vektor so gedreht, dass er dabei auf kürzestem Wege in den zweiten Vektor überführt wird, bewegt sich, sofern alle drei Vektoren ein Rechtssystem bilden, eine im gleichen Sinn gedrehte Schraube mit Rechtsgewinde in Richtung des dritten Vektors.^[3]

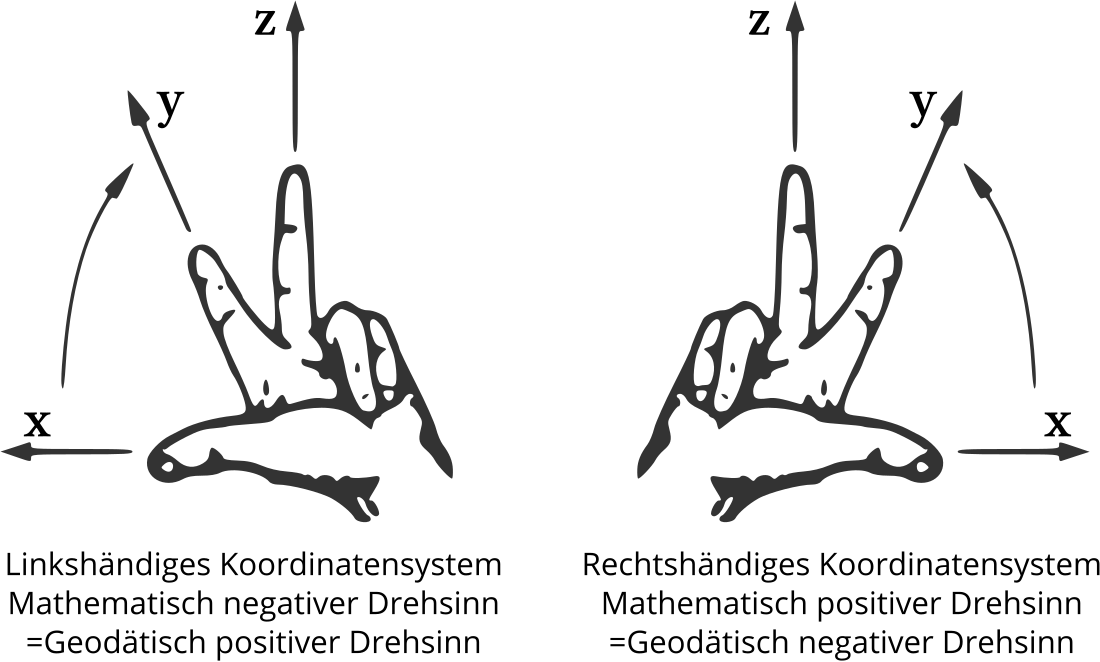
Für 2-dimensionale Systeme kann eine der Drei-Finger-Regel analoge Regel wie folgt formuliert werden: Zeigt der Daumen der nach oben geöffneten rechten (bzw. linken) Hand in die positive ${\displaystyle x}$-Richtung, zeigen bei einem rechtshändigen (bzw. linkshändigen) System alle übrigen Finger in die positive ${\displaystyle y}$-Richtung.

Beispiele

• Die Achsen des dreidimensionalen kartesischen Koordinatensystems bilden in seiner üblichen Achsenorientierung (z. B. ${\displaystyle x}$-Achse zum Betrachter, ${\displaystyle y}$-Achse nach rechts, ${\displaystyle z}$-Achse nach oben; ebenso ${\displaystyle x}$-Achse nach rechts, ${\displaystyle y}$-Achse in die Perspektive und ${\displaystyle z}$-Achse nach oben) ein Rechtssystem.^[2]
• Das geodätische Koordinatensystem ist dagegen, dem Drehsinn beim Kompass folgend, ein Linkssystem.
• Ein ebenfalls weitverbreitetes Linkssystem ist das der Pixelkoordinaten bei Grafikprogrammen, bei denen der Koordinatenursprung (0|0) üblicherweise in der linken oberen Bildschirmecke liegt und die ${\displaystyle x}$-Koordinaten (Grafikspalten) von dort aus nach rechts, die ${\displaystyle y}$-Koordinaten (Grafikzeilen) dagegen nach unten gezählt werden, die Koordinaten eines Bildpunkts bzgl. eines (üblichen) rechtshändigen Systems also zur Bildschirmdarstellung zunächst einmal stets einer entsprechenden Koordinatentransformation unterzogen werden müssen.
• Bei der Rotation eines Körpers bilden der Radialvektor, die Tangentialgeschwindigkeit und der Drehimpuls ein Rechtssystem.
• Bei der Auslenkung eines stromdurchflossenen Leiters in einem Magnetfeld (Leiterschaukel-Versuch) bilden die technische Stromrichtung, die Magnetfeldlinien und die Wirkungsrichtung der Lorentzkraft ein Rechtssystem.

Einzelnachweise und Anmerkungen

1. Walter Gellert, Herbert Küstner, Manfred Hellwich, Herbert Kästner (Hrsg.): Kleine Enzyklopädie Mathematik; Leipzig 1970, S. 342–343.
2. August Schmid, Wilhelm Schweizer (Hrsg.): Analytische Geometrie mit Linearer Algebra. Leistungskurs. Ernst Klett Verlag, Stuttgart 1997, ISBN 3-12-739170-6, S. 36–37.
3. Fast alle praktisch verwendeten Schrauben besitzen Rechtsgewinde – solche mit Linksgewinde dagegen finden nur selten Anwendung, z. B. in Spannschlössern.