Kurvenintegral

Das Kurven-, Linien-, Weg- oder Konturintegral erweitert den gewöhnlichen Integralbegriff für die Integration in der komplexen Ebene (Funktionentheorie) oder im mehrdimensionalen Raum (Vektoranalysis).

Den Weg, die Linie oder die Kurve, über die integriert wird, nennt man den Integrationsweg.

Wegintegrale über geschlossene Kurven werden auch als Ringintegral, Umlaufintegral^[1] oder Zirkulation bezeichnet und mit dem Symbol ${\displaystyle \textstyle \oint }$ geschrieben.

Reelle Wegintegrale

Wegintegral erster Art

Illustration eines Kurvenintegrals erster Art über ein Skalarfeld

Das Wegintegral einer stetigen Funktion

${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$

entlang eines stückweise stetig differenzierbaren Weges

${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$

ist definiert als

${\displaystyle \int \limits _{\gamma }\!f\,\mathrm {d} s:=\int \limits _{a}^{b}\!f(\gamma (t))\,\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t.}$

Dabei bezeichnet ${\displaystyle {\dot {\gamma }}}$ die Ableitung von ${\displaystyle \gamma }$ nach ${\displaystyle t}$ und ${\displaystyle \|{\dot {\gamma }}(t)\|_{2}}$ die euklidische Norm des Vektors ${\displaystyle {\dot {\gamma }}(t)}$.

Die Bildmenge ${\displaystyle {\mathcal {C}}:=\gamma ([a,b])}$ ist eine stückweise glatte Kurve in ${\displaystyle \mathbb {R} ^{n}}$.

Anmerkungen

• Ein Beispiel für eine solche Funktion ${\displaystyle f}$ ist ein Skalarfeld mit kartesischen Koordinaten.
• Ein Weg ${\displaystyle \gamma }$ kann eine Kurve ${\displaystyle {\mathcal {C}}}$ entweder als Ganzes oder auch nur in Abschnitten mehrfach durchlaufen.
• Für ${\displaystyle f\equiv 1}$ ergibt das Wegintegral erster Art die Länge des Weges ${\displaystyle \gamma }$.
• Der Weg ${\displaystyle \gamma }$ bildet u. a. ${\displaystyle a\in \mathbb {R} }$ auf den Anfangspunkt der Kurve ab und ${\displaystyle b\in \mathbb {R} }$ auf deren Endpunkt.
• ${\displaystyle t\in [a,b]}$ ist ein Element der Definitionsmenge von ${\displaystyle \gamma }$ und steht allgemein nicht für die Zeit. ${\displaystyle \mathrm {d} t}$ ist das zugehörige Differential.

Wegintegral zweiter Art

Illustration eines Kurvenintegrals zweiter Art über den Weg ${\displaystyle r}$ in einem Vektorfeld

Das Wegintegral über ein stetiges Vektorfeld

${\displaystyle \mathbf {f} \colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}}$

mit einer ebenfalls so parametrisierten Kurve ist definiert als das Integral über das Skalarprodukt aus ${\displaystyle \mathbf {f} \circ \gamma }$ und ${\displaystyle {\dot {\gamma }}}$:

${\displaystyle \int \limits _{\gamma }\!\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x}$ :=\int \limits _{a}^{b}\!\mathbf {f} (\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t}

Umparametrisierung

Sei ${\displaystyle \varphi \colon [c,d]\to [a,b]}$ eine bijektive, differenzierbare Funktion und somit streng monoton, dann ist ${\displaystyle {\tilde {\gamma }}=\gamma \circ \varphi \colon [c,d]\to \mathbb {R} ^{n}}$ eine Umparametrisierung des Weges ${\displaystyle {\mathcal {C}}=\gamma ([a,b])={\tilde {\gamma }}([c,d])}$. Mithilfe der Kettenregel erhält man für Wegintegrale erster und zweiter Art die Beziehungen

${\displaystyle \int _{\gamma }f\,\mathrm {d} s=\int _{\tilde {\gamma }}f\,\mathrm {d} s,}$

${\displaystyle \int _{\gamma }\mathbf {f} \cdot \mathrm {d} \mathbf {x} =\pm \int _{\tilde {\gamma }}\mathbf {f} \cdot \mathrm {d} \mathbf {x} ,}$

wobei man in der letzten Gleichung auf der rechten Seite ein positives (negatives) Vorzeichen erhält, falls ${\displaystyle \varphi }$ streng monoton wachsend (fallend) ist. Wegintegrale erster Art bleiben also invariant unter Umparametrisierungen.

Für Wegintegrale zweiter Art ist der Integralwert nur invariant unter orientierungserhaltenden Umparametrisierungen, d. h. ${\displaystyle \gamma }$ und ${\displaystyle {\tilde {\gamma }}}$ müssen ${\displaystyle {\mathcal {C}}}$ in derselben Richtung durchlaufen, was ${\displaystyle \gamma (a)={\tilde {\gamma }}(c)}$ und ${\displaystyle \gamma (b)={\tilde {\gamma }}(d)}$ impliziert. Dies ist genau dann gegeben, wenn ${\displaystyle \varphi }$ streng monoton wächst, was wiederum ${\displaystyle \varphi (c)=a,\varphi (d)=b}$ impliziert.

Ist umgekehrt ${\displaystyle \varphi }$ streng monoton fallend, dann gilt ${\displaystyle \varphi (c)=b}$ und ${\displaystyle \varphi (d)=a}$. Die Kurve ${\displaystyle {\mathcal {C}}}$ wird in umgekehrter Richtung durchlaufen und entsprechend sind Start- und Endpunkte der beiden Wege vertauscht, d. h. ${\displaystyle \gamma (a)={\tilde {\gamma }}(d)}$ sowie ${\displaystyle \gamma (b)={\tilde {\gamma }}(c)}$. Während Wegintegrale erster Art invariant unter solchen Umparametrisierungen sind, sind ändert sich bei Wegintegralen zweiter Art das Vorzeichen. Ein Spezialfall einer solchen Umparametrisierung ist gegeben durch ${\displaystyle c=a}$, ${\displaystyle d=b}$ und ${\displaystyle \varphi ^{-}(t)=a+b-t}$. Den entsprechenden rückwärts durchlaufenden Weg bezeichnet man als ${\displaystyle \gamma ^{-}=\gamma \circ \varphi ^{-}}$ und erhält entsprechend die Gleichungen

${\displaystyle \int _{\gamma ^{-}}f\,\mathrm {d} s=\int _{\gamma }f\,\mathrm {d} s\quad {\text{und}}\quad \int _{\gamma ^{-}}\mathbf {f} \cdot \mathrm {d} \mathbf {x} =-\int _{\gamma }\mathbf {f} \cdot \mathrm {d} \mathbf {x} ,}$

Einfluss der Parametrisierung

Umgekehrt sei ${\displaystyle {\mathcal {C}}}$ ein Weg (mit fester Orientierung) und seien ${\displaystyle \gamma \colon [a,b]\to {\mathcal {C}},{\tilde {\gamma }}\colon [a,b]\to {\mathcal {C}}}$ zwei Parametrisierungen (mit derselben Orientierung), die (bis auf einzelnen Punkte) bijektiv sind, dann lässt sich der Weg mittels ${\displaystyle \varphi$ :=\gamma ^{-1}\circ {\tilde {\gamma }}\colon [c,d]\to [a,b]} umparametrisieren. Entsprechend haben die Integrale ${\displaystyle \int _{\gamma }f\,\mathrm {d} s}$, ${\displaystyle \int _{\gamma }\mathbf {f} \cdot \mathrm {d} \mathbf {x} }$ denselben Wert für alle Parametrisierungen ${\displaystyle \gamma }$ (mit entsprechender Orientierung für Wegintegrale zweiter Art). Dies rechtfertigt den Namen Kurvenintegral und die Notation ${\displaystyle \int _{\mathcal {C}}\equiv \int _{\gamma }}$.

Kurvenintegrale

Da eine Kurve ${\displaystyle {\mathcal {C}}}$ das Bild eines Weges ${\displaystyle \gamma }$ ist, entsprechen die Definitionen der Kurvenintegrale im Wesentlichen den Wegintegralen.

Kurvenintegral 1. Art:

${\displaystyle \int \limits _{\mathcal {C}}\!f\,\mathrm {d} s:=\int \limits _{a}^{b}\!f(\gamma (t))\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t}$

Kurvenintegral 2. Art:

${\displaystyle \int \limits _{\mathcal {C}}\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x}$ :=\int \limits _{a}^{b}\mathbf {f} (\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t}

Ein Spezialfall ist wieder die Länge der durch ${\displaystyle \gamma }$ parametrisierten Kurve ${\displaystyle {\mathcal {C}}}$:

${\displaystyle \mathrm {L{\ddot {a}}nge\ von\ } {\mathcal {C}}=|{\mathcal {C}}|=L({\mathcal {C}})=\int \limits _{\mathcal {C}}\mathrm {d} s=\int \limits _{a}^{b}\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t,}$

welche nach obigen Aussagen unabhängig von der Parametrisierung ${\displaystyle \gamma }$ und deren Orientierung ist.

Wegelement und Längenelement

Der in den Kurvenintegralen erster Art auftretende Ausdruck

${\displaystyle \mathrm {d} s=\|{\dot {\gamma }}(t)\|_{2}\,\mathrm {d} t}$

heißt skalares Wegelement oder Längenelement. Der in den Kurvenintegralen zweiter Art auftretende Ausdruck

${\displaystyle \mathrm {d} \mathbf {x} ={\dot {\gamma }}(t)\,\mathrm {d} t}$

heißt vektorielles Wegelement.

Rechenregeln

Seien ${\displaystyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )}$, ${\displaystyle \int \limits _{\gamma }\mathbf {g} (\mathbf {x} )}$ Kurvenintegrale gleicher Art (also entweder beide erster oder beide zweiter Art), sei das Urbild der beiden Funktionen ${\displaystyle \mathbf {f} }$ und ${\displaystyle \mathbf {g} }$ von gleicher Dimension und sei ${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$. Dann gelten für ${\displaystyle \alpha }$, ${\displaystyle \beta \in \mathbb {R} }$ und ${\displaystyle c\in \mathbb {[} a,b]}$ die folgenden Rechenregeln:

• ${\displaystyle \alpha \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )+\beta \int \limits _{\gamma }\mathbf {g} (\mathbf {x} )=\int \limits _{\gamma }(\alpha \mathbf {f} (\mathbf {x} )+\beta \mathbf {g} (\mathbf {x} ))}$    (Linearität)

• ${\displaystyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )=\int \limits _{\gamma |_{[a,c]}}\mathbf {f} (\mathbf {x} )+\int \limits _{\gamma |_{[c,b]}}\mathbf {f} (\mathbf {x} )}$    (Zerlegungsadditivität)

Seinen ${\displaystyle \gamma _{1}\colon [a,b]\to \mathbb {R} ^{n}}$ und ${\displaystyle \gamma _{2}\colon [c,d]\to \mathbb {R} ^{n}}$ mit ${\displaystyle \gamma _{1}(b)=\gamma _{2}(c)}$, d. h. der Endpunkt von ${\displaystyle \gamma _{1}}$ ist der Startpunkt von ${\displaystyle \gamma _{2}}$, dann definiert

${\displaystyle \gamma _{1}\oplus \gamma _{2}\colon [a,b+d-c]\to \mathbb {R} ^{n},t\to (\gamma _{1}\oplus \gamma _{2})(t):={\begin{cases}\gamma _{1}(t),\quad &{\text{für}}\,a\leq t\leq b\\\gamma _{2}(t-b+c),\quad &{\text{für}}\,b<t\leq b+d-c\end{cases}}}$

einen stückweise differenzierbaren Weg, der ${\displaystyle \gamma _{1}}$ und ${\displaystyle \gamma _{2}}$ miteinander verknüpft. Diese Verknüpfung hat die Eigenschaften

${\displaystyle (\gamma _{1}\oplus \gamma _{2})\oplus \gamma _{3}=\gamma _{1}\oplus (\gamma _{2}\oplus \gamma _{3})\quad {\text{(Assoziativität)}}}$

${\displaystyle (\gamma _{1}\oplus \gamma _{2})^{-}=\gamma _{2}^{-}\oplus \gamma _{1}^{-}}$

und man erhält auch hier Zerlegungsadditivität für beide Typen von Wegintegralen:

${\displaystyle \int _{\gamma _{1}\oplus \gamma _{2}}f\,\mathrm {d} s=\int _{\gamma _{1}}f\,\mathrm {d} s+\int _{\gamma _{2}}f\,\mathrm {d} s}$

${\displaystyle \int _{\gamma _{1}\oplus \gamma _{2}}\mathbf {f} \cdot \mathrm {d} \mathbf {x} =\int _{\gamma _{1}}\mathbf {f} \cdot \mathrm {d} \mathbf {x} +\int _{\gamma _{2}}\mathbf {f} \cdot \mathrm {d} \mathbf {x} }$

Aus der Dreiecksungleichung für Integrale und der Cauchy-Schwarz-Ungleichung folgt die Dreiecksungleichung für Wegintegrale:

${\displaystyle \left|\int _{\gamma }\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x} \right|\leq \int _{\gamma }\left\|\mathbf {f} (\mathbf {x} )\right\|_{2}\,\mathrm {d} s\leq L({\mathcal {C}})\,\sup _{\mathbf {x} \in {\mathcal {C}}}\left\|\mathbf {f} (\mathbf {x} )\right\|_{2},}$

wobei ${\displaystyle {\mathcal {C}}=\gamma ([a,b])}$ den durch ${\displaystyle \gamma }$ parametrisierten Weg bezeichnet und ${\displaystyle L({\mathcal {C}})}$ dessen Länge (wie oben definiert). Man beachte, dass bei der ersten Ungleichung Wegintegral zweiter Art gegen ein Wegintegral erster Art abgeschätzt wird. Analog gilt die Dreiecksungleichung

${\displaystyle \left|\int _{\gamma }f(\mathbf {x} )\,\mathrm {d} s\right|\leq \int _{\gamma }\left|f(\mathbf {x} )\right|\,\mathrm {d} s\leq L({\mathcal {C}})\,\sup _{\mathbf {x} \in {\mathcal {C}}}\left|f(\mathbf {x} )\right|}$

für Wegintegrale erster Art.

Notation für Kurvenintegrale von geschlossenen Kurven

Ist ${\displaystyle \gamma }$ ein geschlossener Weg, so schreibt man

statt ${\displaystyle \displaystyle \int \limits _{\gamma }}$ auch ${\displaystyle \displaystyle \oint \limits _{\gamma }}$

und analog für geschlossene Kurven ${\displaystyle {\mathcal {C}}}$

statt ${\displaystyle \displaystyle \int \limits _{\mathcal {C}}}$ auch ${\displaystyle \displaystyle \oint \limits _{\mathcal {C}}}$.

Mit dem Kreis im Integral möchte man deutlich machen, dass ${\displaystyle \gamma }$ geschlossen ist. Der einzige Unterschied liegt hierbei in der Notation.

Beispiele

• Ist ${\displaystyle {\mathcal {C}}}$ der Graph einer Funktion ${\displaystyle f\colon [a,b]\to \mathbb {R} }$, so wird diese Kurve durch den Weg

${\displaystyle \gamma \colon [a,b]\to \mathbb {R} ^{2},\quad t\mapsto (t,f(t))}$

parametrisiert. Wegen

${\displaystyle \|{\dot {\gamma }}(t)\|_{2}={\sqrt {1+f'(t)^{2}}}}$

ist die Länge der Kurve gleich

${\displaystyle \int \limits _{\mathcal {C}}\mathrm {d} s=\int \limits _{a}^{b}{\sqrt {1+f'(t)^{2}}}\,\mathrm {d} t.}$

• Eine Ellipse mit großer Halbachse ${\displaystyle a}$ und kleiner Halbachse ${\displaystyle b}$ wird durch ${\displaystyle (a\cos t,\,b\sin t)}$ für ${\displaystyle t\in [0,2\pi ]}$ parametrisiert. Ihr Umfang ist also

${\displaystyle \int \limits _{0}^{2\pi }{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t=4a\int \limits _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}\cos ^{2}t}}\;\mathrm {d} t}$.

Dabei bezeichnet ${\displaystyle \varepsilon }$ die numerische Exzentrizität ${\displaystyle {\sqrt {1-b^{2}/a^{2}}}}$ der Ellipse. Das Integral auf der rechten Seite wird aufgrund dieses Zusammenhanges als elliptisches Integral bezeichnet.

Wegunabhängigkeit

Ist ein Vektorfeld ${\displaystyle \mathbf {F} }$ ein Gradientenfeld, d. h., ${\displaystyle \mathbf {F} }$ ist der Gradient eines skalaren Feldes ${\displaystyle V}$, mit

${\displaystyle \mathbf {\nabla } V=\mathbf {F} }$,

so gilt für die Ableitung der Verkettung von ${\displaystyle V}$ und ${\displaystyle \mathbf {r} (t)}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {r} (t))=\mathbf {\nabla } V(\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)=\mathbf {F} (\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)}$,

was gerade dem Integranden des Wegintegrals über ${\displaystyle \mathbf {F} }$ auf ${\displaystyle \mathbf {r} (t)}$ entspricht. Daraus folgt für eine gegebene Kurve ${\displaystyle {\mathcal {S}}}$

${\displaystyle \int \limits _{\mathcal {S}}\mathbf {F} (\mathbf {x} )\cdot \,\mathrm {d} \mathbf {x} =\int \limits _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)\,\mathrm {d} t=\int \limits _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {r} (t))\,\mathrm {d} t=V(\mathbf {r} (b))-V(\mathbf {r} (a)).}$

Zwei beliebige Kurven ${\displaystyle {\mathcal {S}}1}$ und ${\displaystyle {\mathcal {S}}2}$ in einem Gradientenfeld

Dies bedeutet, dass das Integral von ${\displaystyle \mathbf {F} }$ über ${\displaystyle {\mathcal {S}}}$ ausschließlich von den Punkten ${\displaystyle \mathbf {r} (b)}$ und ${\displaystyle \mathbf {r} (a)}$ abhängt und der Weg dazwischen irrelevant für das Ergebnis ist. Aus diesem Grund wird das Integral eines Gradientenfeldes als „wegunabhängig“ bezeichnet.

Insbesondere gilt für das Ringintegral über die geschlossene Kurve ${\displaystyle {\mathcal {S}}}$ mit zwei beliebigen Wegen ${\displaystyle {\mathcal {S}}_{1}}$ und ${\displaystyle {\mathcal {S}}_{2}}$:

${\displaystyle \oint \limits _{\mathcal {S}}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} =\int \limits _{1,{\mathcal {S}}_{1}}^{2}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} +\int \limits _{2,{\mathcal {S}}_{2}}^{1}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} =0}$

Dies ist insbesondere in der Physik von großer Bedeutung, da beispielsweise die Gravitation diese Eigenschaften besitzt. Da die Energie in diesen Kraftfeldern stets eine Erhaltungsgröße ist, werden sie in der Physik als konservative Kraftfelder bezeichnet. Das skalare Feld ${\displaystyle V}$ ist dabei das Potential oder die potentielle Energie. Konservative Kraftfelder erhalten die mechanische Energie, d. i. die Summe aus kinetischer Energie und potentieller Energie. Gemäß dem obigen Integral wird auf einer geschlossenen Kurve insgesamt eine Arbeit von 0 J aufgebracht.

Wegunabhängigkeit lässt sich auch mit Hilfe der Integrabilitätsbedingung zeigen und gilt im Allgemeinen nur auf einfach zusammenhängenden Gebieten bzw. nur zwischen zueinander homotopen Kurven ${\displaystyle {\mathcal {S}}_{1}}$ und ${\displaystyle {\mathcal {S}}_{2}}$.

Die Kurve ${\displaystyle \gamma }$ umläuft das Zentrum ${\displaystyle z_{0}}$ zweimal

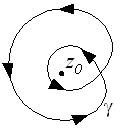
Ist das Vektorfeld nur in einer (kleinen) Umgebung ${\displaystyle U}$ eines Punktes nicht als Gradientenfeld darstellbar, so ist das geschlossene Wegintegral von Kurven außerhalb von ${\displaystyle U}$ proportional zur Windungszahl um diesen Punkt und ansonsten unabhängig vom genauen Verlauf der Kurve (siehe Algebraische Topologie: Methodik).

Komplexe Wegintegrale

Integrale komplexwertiger Funktionen

Ist ${\displaystyle f\colon [a,b]\to \mathbb {C} }$ eine komplexwertige Funktion, dann nennt man ${\displaystyle f}$ integrierbar, wenn ${\displaystyle \operatorname {Re} f}$ und ${\displaystyle \operatorname {Im} f}$ integrierbar sind. Man definiert

${\displaystyle \int \limits _{a}^{b}f(x)\mathrm {d} x:=\int \limits _{a}^{b}\operatorname {Re} f(x)\mathrm {d} x+\mathrm {i} \int \limits _{a}^{b}\operatorname {Im} f(x)\mathrm {d} x}$.

Das Integral ist damit ${\displaystyle \mathbb {C} }$-linear. Ist ${\displaystyle f}$ im Intervall ${\displaystyle [a,b]}$ stetig und ${\displaystyle F}$ eine Stammfunktion von ${\displaystyle f}$, so gilt wie im Reellen

${\displaystyle \int \limits _{a}^{b}f(x)\mathrm {d} x=F(b)-F(a)}$.

Wegintegrale komplexer Funktionen

Der Integralbegriff wird nun auf die komplexe Ebene wie folgt erweitert: Ist ${\displaystyle f\colon U\to \mathbb {C} }$ eine komplexwertige Funktion auf einem Gebiet ${\displaystyle U\subseteq \mathbb {C} }$, und ist ${\displaystyle \gamma \colon [0,1]\to U}$ ein stückweise stetig differenzierbarer Weg in ${\displaystyle U}$, so ist das Wegintegral von ${\displaystyle f}$ entlang des Weges ${\displaystyle \gamma }$ definiert als

${\displaystyle \int \limits _{\gamma }f:=\int \limits _{\gamma }f(z)\,\mathrm {d} z:=\int \limits _{0}^{1}f(\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t.}$

Der Malpunkt bezeichnet hier komplexe Multiplikation.

Folgerungen

Die zentrale Aussage über Wegintegrale komplexer Funktionen ist der Cauchysche Integralsatz: Für eine holomorphe Funktion ${\displaystyle f}$ hängt das Wegintegral nur von der Homotopieklasse von ${\displaystyle \gamma }$ ab. Ist ${\displaystyle U}$ einfach zusammenhängend, so hängt das Integral also überhaupt nicht von ${\displaystyle \gamma }$, sondern nur von Anfangs- und Endpunkt ab.

Beziehung zu reellen Wegintegralen

Definiert man

${\displaystyle {\tilde {U}}:=\left\{(x,y)\in \mathbb {R} ^{2}\mid x+iy\in U\right\}\subset \mathbb {R} ^{2},}$

${\displaystyle {\tilde {f}}:{\tilde {U}}\rightarrow \mathbb {R} ^{2},(x,y)\rightarrow {\tilde {f}}(x,y):=\left(u(x,y),v(x,y)\right):=\left(\Re {f(x+iy)},\Im {f(x+iy)}\right)}$

${\displaystyle {\tilde {\gamma }}:[0,1]\rightarrow {\tilde {U}},t\rightarrow {\tilde {\gamma }}(t):=\left(\alpha (t),\beta (t)\right):=\left(\Re {\gamma (t)},\Im {\gamma (t)}\right)}$

als reelle Entsprechungen von ${\displaystyle U}$, ${\displaystyle f}$ und ${\displaystyle \gamma }$ mit ${\displaystyle u,v:{\tilde {U}}\rightarrow \mathbb {R} }$ bzw. ${\displaystyle \alpha ,\beta$ :[0,1]\rightarrow \mathbb {R} } Real- und Imaginärteil von ${\displaystyle f}$ bzw. ${\displaystyle \gamma }$, dann gilt nach obiger Definition

${\displaystyle {\begin{aligned}\int \limits _{\gamma }f(z)\,\mathrm {d} z=&\int \limits _{0}^{1}f(\gamma (t))\cdot {\dot {\gamma }}(t)\,\mathrm {d} t=\int \limits _{0}^{1}\left[u({\tilde {\gamma }}(t))+iv({\tilde {\gamma }}(t))\right]\cdot \left[{\dot {\alpha }}(t)+i{\dot {\beta }}(t)\right]\,\mathrm {d} t\\=&\int \limits _{0}^{1}u({\tilde {\gamma }}(t)){\dot {\alpha }}(t)-{\dot {\beta }}(t)v({\tilde {\gamma }}(t))\,\mathrm {d} t+i\int \limits _{0}^{1}v({\tilde {\gamma }}(t)){\dot {\alpha }}(t)+{\dot {\beta }}(t)u({\tilde {\gamma }}(t))\,\mathrm {d} t\\=&\int \limits _{0}^{1}{\begin{pmatrix}u({\tilde {\gamma }}(t))\\-v({\tilde {\gamma }}(t))\end{pmatrix}}\cdot {\tilde {\gamma }}(t)\,\mathrm {d} t+i\int \limits _{0}^{1}{\begin{pmatrix}v({\tilde {\gamma }}(t))\\u({\tilde {\gamma }}(t))\end{pmatrix}}\cdot {\tilde {\gamma }}(t)\,\mathrm {d} t\\=&\int \limits _{\tilde {\gamma }}\mathbf {g} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x} +i\int \limits _{\tilde {\gamma }}\mathbf {h} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x} ,\end{aligned}}}$

wobei im letzten Schritt die Vektorfelder

${\displaystyle \mathbf {g}$ :{\tilde {U}}\rightarrow \mathbb {R} ^{2},\mathbf {x} =(x,y)\rightarrow \mathbf {g} (x,y):={\begin{pmatrix}u(x,y)\\-v(x,y)\end{pmatrix}},\quad \mathbf {h} :{\tilde {U}}\rightarrow \mathbb {R} ^{2},\mathbf {x} =(x,y)\rightarrow \mathbf {h} (x,y):={\begin{pmatrix}v(x,y)\\u(x,y)\end{pmatrix}}}

eingeführt wurden. Das heißt das Wegintegral einer komplexen Funktion kann auch als Summe zweier reellen Wegintegrale zweiter Art dargestellt werden.

Aus der letzten Darstellung folgt auch unmittelbar der Cauchysche Integralsatz, denn für eine holomorphe Funktion ${\displaystyle f}$ erfüllen ${\displaystyle u}$ und ${\displaystyle v}$ die Cauchy-Riemannschen Differentialgleichungen. Da diese äquivalent zur Integrabilitätsbedingungen von ${\displaystyle \mathbf {g} }$ und ${\displaystyle \mathbf {h} }$ sind, ist das komplexe Wegintegral über ${\displaystyle f}$ wegunabhängig, d. h. sein Wert ist invariant unter homotopen Wegänderungen ${\displaystyle \gamma _{1}\rightarrow \gamma _{2}}$.

Eigenschaften

Eigenschaften wie Linearität, Zerlegungsadditivität und Invarianz unter Umparametrisierung folgen nach der letzten Darstellung direkt aus den entsprechenden Beziehungen für reelle Kurvenintegrale.

Analog zum reellen Fall definiert man die Länge des Weges ${\displaystyle \gamma }$ durch

${\displaystyle \operatorname {L} (\gamma ):=\int \limits _{0}^{1}\left|{\dot {\gamma }}(t)\right|\mathrm {d} t}$.

Auch für komplexe Kurvenintegrale gilt die Dreiecksungleichung

${\displaystyle \left|\int _{\gamma }f(z)\,\mathrm {d} z\right|\leq \int _{\tilde {\gamma }}\left\|{\tilde {f}}(x,y)\right\|_{2}\,\mathrm {d} s(x,y)\leq \operatorname {L} (\gamma )\cdot \sup _{z\in \gamma ([0,1])}\left|f(z)\right|}$,

Das zweite Integral ist dabei ein zweidimensionales, reelles Wegintegral erster Art, wobei ${\displaystyle {\tilde {f}}}$ und ${\displaystyle {\tilde {\gamma }}}$ wie oben die reellen Versionen von ${\displaystyle f}$ und ${\displaystyle \gamma }$ sind. Die verkürzte Ungleichung

${\displaystyle \left|\int _{\gamma }f(z)\,\mathrm {d} z\right|\leq C\cdot \operatorname {L} (\gamma )\quad {\text{mit}}\quad C=\sup _{z\in \gamma ([0,1])}\left|f(z)\right|<\infty }$

wird als Standardabschätzung bezeichnet und ist vor allem für theoretische Zwecke von besonderer Bedeutung.

Wie im reellen Fall ist das Wegintegral unabhängig von der Parametrisierung des Weges ${\displaystyle \gamma }$, d. h., es ist nicht zwingend notwendig, ${\displaystyle [0,1]}$ als Parameterbereich zu wählen, wie sich durch Substitution zeigen lässt. Dies erlaubt die Definition komplexer Kurvenintegrale, indem man den obigen Formeln den Weg ${\displaystyle \gamma }$ durch eine Kurve ${\displaystyle {\mathcal {C}}}$ in ${\displaystyle \mathbb {C} }$ ersetzt.

Siehe dagegen

• Pfadintegral

Literatur

• Harro Heuser: Lehrbuch der Analysis – Teil 2. 1981, 5. Auflage, Teubner 1990, ISBN 3-519-42222-0. S. 369, Satz 180.1; S. 391, Satz 184.1; S. 393, Satz 185.1.

Weblinks

Wiktionary: Kurvenintegral – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Kurvenintegrale bei Matroids Matheplanet