Loading AI tools
Class of quartic plane curves From Wikipedia, the free encyclopedia
In geometry, a Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points (foci) is constant. This may be contrasted with an ellipse, for which the sum of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2.
Cassini ovals are named after the astronomer Giovanni Domenico Cassini who studied them in the late 17th century.[1] Cassini believed that a planet orbiting around another body traveled on one of these ovals, with the body it orbited around at one focus of the oval.[2] Other names include Cassinian ovals, Cassinian curves and ovals of Cassini.

A Cassini oval is a set of points, such that for any point of the set, the product of the distances to two fixed points is a constant, usually written as where :
As with an ellipse, the fixed points are called the foci of the Cassini oval.
If the foci are (a, 0) and (−a, 0), then the equation of the curve is
When expanded this becomes
The equivalent polar equation is

The curve depends, up to similarity, on e = b/a. When e < 1, the curve consists of two disconnected loops, each of which contains a focus. When e = 1, the curve is the lemniscate of Bernoulli having the shape of a sideways figure eight with a double point (specifically, a crunode) at the origin.[3][4] When e > 1, the curve is a single, connected loop enclosing both foci. It is peanut-shaped for and convex for [5] The limiting case of a → 0 (hence e → ∞), in which case the foci coincide with each other, is a circle.
The curve always has x-intercepts at ± c where c2 = a2 + b2. When e < 1 there are two additional real x-intercepts and when e > 1 there are two real y-intercepts, all other x- and y-intercepts being imaginary.[6]
The curve has double points at the circular points at infinity, in other words the curve is bicircular. These points are biflecnodes, meaning that the curve has two distinct tangents at these points and each branch of the curve has a point of inflection there. From this information and Plücker's formulas it is possible to deduce the Plücker numbers for the case e ≠ 1: degree = 4, class = 8, number of nodes = 2, number of cusps = 0, number of double tangents = 8, number of points of inflection = 12, genus = 1.[7]
The tangents at the circular points are given by x ± iy = ± a which have real points of intersection at (± a, 0). So the foci are, in fact, foci in the sense defined by Plücker.[8] The circular points are points of inflection so these are triple foci. When e ≠ 1 the curve has class eight, which implies that there should be a total of eight real foci. Six of these have been accounted for in the two triple foci and the remaining two are at So the additional foci are on the x-axis when the curve has two loops and on the y-axis when the curve has a single loop.[9]

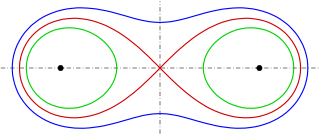
Orthogonal trajectories of a given pencil of curves are curves which intersect all given curves orthogonally. For example the orthogonal trajectories of a pencil of confocal ellipses are the confocal hyperbolas with the same foci. For Cassini ovals one has:
Proof:
For simplicity one chooses .
These conic sections have no points with the y-axis in common and intersect the x-axis at . Their discriminants show that these curves are hyperbolas. A more detailed investigation reveals that the hyperbolas are rectangular. In order to get normals, which are independent from parameter the following implicit representation is more convenient A simple calculation shows that for all . Hence the Cassini ovals and the hyperbolas intersect orthogonally.
Remark:
The image depicting the Cassini ovals and the hyperbolas looks like the equipotential curves of two equal point charges together with the lines of the generated electrical field. But for the potential of two equal point charges one has . (See Implicit curve.) Instead these curves actually correspond to the (plane sections of) equipotential sets of two infinite wires with equal constant line charge density, or alternatively, to the level sets of the sums of the Green’s functions for the Laplacian in two dimensions centered at the foci.
The single-loop and double loop Cassini curves can be represented as the orthogonal trajectories of each other when each family is coaxal but not confocal. If the single-loops are described by then the foci are variable on the axis if , if ; if the double-loops are described by then the axes are, respectively, and . Each curve, up to similarity, appears twice in the image, which now resembles the field lines and potential curves for four equal point charges, located at and . Further, the portion of this image in the upper half-plane depicts the following situation: The double-loops are a reduced set of congruence classes for the central Steiner conics in the hyperbolic plane produced by direct collineations;[10] and each single-loop is the locus of points such that the angle is constant, where and is the foot of the perpendicular through on the line described by .
The second lemniscate of the Mandelbrot set is a Cassini oval defined by the equation Its foci are at the points c on the complex plane that have orbits where every second value of z is equal to zero, which are the values 0 and −1.

Cassini ovals appear as planar sections of tori, but only when the cutting plane is parallel to the axis of the torus and its distance to the axis equals the radius of the generating circle (see picture).
The intersection of the torus with equation
and the plane yields
After partially resolving the first bracket one gets the equation
which is the equation of a Cassini oval with parameters and .
Cassini's method is easy to generalize to curves and surfaces with an arbitrarily many defining points:
describes in the planar case an implicit curve and in 3-space an implicit surface.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.