Top Qs
Timeline
Chat
Perspective
Continuous uniform distribution
Uniform distribution on an interval From Wikipedia, the free encyclopedia
Remove ads
In probability theory and statistics, the continuous uniform distributions or rectangular distributions are a family of symmetric probability distributions. Such a distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds.[1] The bounds are defined by the parameters, and which are the minimum and maximum values. The interval can either be closed (i.e. ) or open (i.e. ).[2] Therefore, the distribution is often abbreviated where stands for uniform distribution.[1] The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable under no constraint other than that it is contained in the distribution's support.[3]
Remove ads
Definitions
Probability density function
The probability density function of the continuous uniform distribution is
The values of at the two boundaries and are usually unimportant, because they do not alter the value of over any interval nor of nor of any higher moment. Sometimes they are chosen to be zero, and sometimes chosen to be The latter is appropriate in the context of estimation by the method of maximum likelihood. In the context of Fourier analysis, one may take the value of or to be because then the inverse transform of many integral transforms of this uniform function will yield back the function itself, rather than a function which is equal "almost everywhere", i.e. except on a set of points with zero measure. Also, it is consistent with the sign function, which has no such ambiguity.
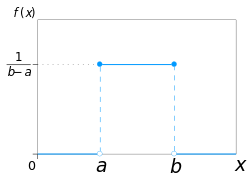
Any probability density function integrates to so the probability density function of the continuous uniform distribution is graphically portrayed as a rectangle where is the base length and is the height. As the base length increases, the height (the density at any particular value within the distribution boundaries) decreases.[4]
In terms of mean and variance the probability density function of the continuous uniform distribution is
Cumulative distribution function
The cumulative distribution function of the continuous uniform distribution is:
Its inverse is:
In terms of mean and variance the cumulative distribution function of the continuous uniform distribution is:
its inverse is:
Example 1. Using the continuous uniform distribution function
For a random variable find
In a graphical representation of the continuous uniform distribution function the area under the curve within the specified bounds, displaying the probability, is a rectangle. For the specific example above, the base would be and the height would be [5]
Example 2. Using the continuous uniform distribution function (conditional)
For a random variable find
The example above is a conditional probability case for the continuous uniform distribution: given that is true, what is the probability that Conditional probability changes the sample space, so a new interval length has to be calculated, where and [5] The graphical representation would still follow Example 1, where the area under the curve within the specified bounds displays the probability; the base of the rectangle would be and the height would be [5]
Generating functions
Moment-generating function
The moment-generating function of the continuous uniform distribution is:[6] from which we may calculate the raw moments
For a random variable following the continuous uniform distribution, the expected value is and the variance is
For the special case the probability density function of the continuous uniform distribution is:
the moment-generating function reduces to the simple form:
Cumulant-generating function
For the -th cumulant of the continuous uniform distribution on the interval is where is the -th Bernoulli number.[7]
Standard uniform distribution
The continuous uniform distribution with parameters and i.e. is called the standard uniform distribution.
One interesting property of the standard uniform distribution is that if has a standard uniform distribution, then so does This property can be used for generating antithetic variates, among other things. In other words, this property is known as the inversion method where the continuous standard uniform distribution can be used to generate random numbers for any other continuous distribution.[4] If is a uniform random number with standard uniform distribution, i.e. with then generates a random number from any continuous distribution with the specified cumulative distribution function [4]
Relationship to other functions
As long as the same conventions are followed at the transition points, the probability density function of the continuous uniform distribution may also be expressed in terms of the Heaviside step function as:
or in terms of the rectangle function as:
There is no ambiguity at the transition point of the sign function. Using the half-maximum convention at the transition points, the continuous uniform distribution may be expressed in terms of the sign function as:
Remove ads
Properties
Summarize
Perspective
Moments
The mean (first raw moment) of the continuous uniform distribution is:
The second raw moment of this distribution is:
In general, the -th raw moment of this distribution is:
The variance (second central moment) of this distribution is:
Order statistics
Let be an i.i.d. sample from and let be the -th order statistic from this sample.
has a beta distribution, with parameters and
The expected value is:
This fact is useful when making Q–Q plots.
The variance is:
Uniformity
The probability that a continuously uniformly distributed random variable falls within any interval of fixed length is independent of the location of the interval itself (but it is dependent on the interval size ), so long as the interval is contained in the distribution's support.
Indeed, if and if is a subinterval of with fixed then: which is independent of This fact motivates the distribution's name.
Uniform distribution on more general sets
The uniform distribution can be generalized to sets more general than intervals.
Formally, let be a Borel set of positive, finite Lebesgue measure i.e. The uniform distribution on can be specified by defining the probability density function to be zero outside and constantly equal to on
An interesting special case is when the set S is a simplex. It is possible to obtain a uniform distribution on the standard n-vertex simplex in the following way.[8]: Thm.4.1 take n independent random variables with the same exponential distribution; denote them by X1,...,Xn; and let Yi := Xi / (sumi Xi). Then, the vector Y1,...,Yn is uniformly distributed on the simplex.
Remove ads
Related distributions
- If X has a standard uniform distribution, then by the inverse transform sampling method, Y = − λ−1 ln(X) has an exponential distribution with (rate) parameter λ.
- If X has a standard uniform distribution, then Y = Xn has a beta distribution with parameters (1/n,1). As such,
- The standard uniform distribution is a special case of the beta distribution, with parameters (1,1).
- The Irwin–Hall distribution is the sum of n i.i.d. U(0,1) distributions.
- The Bates distribution is the average of n i.i.d. U(0,1) distributions.
- The sum of two independent uniform distributions U1(a,b)+U2(c,d) yields a trapezoidal distribution, symmetric about its mean, on the support [a+c,b+d]. The plateau has width equals to the absolute different of the width of U1 and U2. The width of the sloped parts corresponds to the width of the narrowest uniform distribution.
- If the uniform distributions have the same width w, the result is a triangular distribution, symmetric about its mean, on the support [a+c,a+c+2w].
- The sum of two independent, equally distributed, uniform distributions U1(a,b)+U2(a,b) yields a symmetric triangular distribution on the support [2a,2b].
- The distance between two i.i.d. uniform random variables |U1(a,b)-U2(a,b)| also has a triangular distribution, although not symmetric, on the support [0,b-a].
Statistical inference
Estimation of parameters
Estimation of maximum
Minimum-variance unbiased estimator
Given a uniform distribution on with unknown the minimum-variance unbiased estimator (UMVUE) for the maximum is: where is the sample maximum and is the sample size, sampling without replacement (though this distinction almost surely makes no difference for a continuous distribution). This follows for the same reasons as estimation for the discrete distribution, and can be seen as a very simple case of maximum spacing estimation. This problem is commonly known as the German tank problem, due to application of maximum estimation to estimates of German tank production during World War II.
Method of moments estimator
The method of moments estimator is: where is the sample mean.
Maximum likelihood estimator
The maximum likelihood estimator is: where is the sample maximum, also denoted as the maximum order statistic of the sample.
Estimation of minimum
Given a uniform distribution on with unknown a, the maximum likelihood estimator for a is: , the sample minimum.[9]
Estimation of midpoint
The midpoint of the distribution, is both the mean and the median of the uniform distribution. Although both the sample mean and the sample median are unbiased estimators of the midpoint, neither is as efficient as the sample mid-range, i.e. the arithmetic mean of the sample maximum and the sample minimum, which is the UMVU estimator of the midpoint (and also the maximum likelihood estimate).
Confidence interval
For the maximum
Let be a sample from where is the maximum value in the population. Then has the Lebesgue–Borel density [10]
where is the indicator function of
The confidence interval given before is mathematically incorrect, as cannot be solved for without knowledge of . However, one can solve for for any unknown but valid one then chooses the smallest possible satisfying the condition above. Note that the interval length depends upon the random variable
Remove ads
Occurrence and applications
Summarize
Perspective
The probabilities for uniform distribution function are simple to calculate due to the simplicity of the function form.[2] Therefore, there are various applications that this distribution can be used for as shown below: hypothesis testing situations, random sampling cases, finance, etc. Furthermore, generally, experiments of physical origin follow a uniform distribution (e.g. emission of radioactive particles).[1] However, it is important to note that in any application, there is the unchanging assumption that the probability of falling in an interval of fixed length is constant.[2]
Economics example for uniform distribution
In the field of economics, usually demand and replenishment may not follow the expected normal distribution. As a result, other distribution models are used to better predict probabilities and trends such as Bernoulli process.[11] But according to Wanke (2008), in the particular case of investigating lead-time for inventory management at the beginning of the life cycle when a completely new product is being analyzed, the uniform distribution proves to be more useful.[11] In this situation, other distribution may not be viable since there is no existing data on the new product or that the demand history is unavailable so there isn't really an appropriate or known distribution.[11] The uniform distribution would be ideal in this situation since the random variable of lead-time (related to demand) is unknown for the new product but the results are likely to range between a plausible range of two values.[11] The lead-time would thus represent the random variable. From the uniform distribution model, other factors related to lead-time were able to be calculated such as cycle service level and shortage per cycle. It was also noted that the uniform distribution was also used due to the simplicity of the calculations.[11]
Sampling from an arbitrary distribution
The uniform distribution is useful for sampling from arbitrary distributions. A general method is the inverse transform sampling method, which uses the cumulative distribution function (CDF) of the target random variable. This method is very useful in theoretical work. Since simulations using this method require inverting the CDF of the target variable, alternative methods have been devised for the cases where the CDF is not known in closed form. One such method is rejection sampling.
The normal distribution is an important example where the inverse transform method is not efficient. However, there is an exact method, the Box–Muller transformation, which uses the inverse transform to convert two independent uniform random variables into two independent normally distributed random variables.
Quantization error
In analog-to-digital conversion, a quantization error occurs. This error is either due to rounding or truncation. When the original signal is much larger than one least significant bit (LSB), the quantization error is not significantly correlated with the signal, and has an approximately uniform distribution. The RMS error therefore follows from the variance of this distribution.
Remove ads
Random variate generation
There are many applications in which it is useful to run simulation experiments. Many programming languages come with implementations to generate pseudo-random numbers which are effectively distributed according to the standard uniform distribution.
On the other hand, the uniformly distributed numbers are often used as the basis for non-uniform random variate generation.
If is a value sampled from the standard uniform distribution, then the value follows the uniform distribution parameterized by and as described above.
Remove ads
History
While the historical origins in the conception of uniform distribution are inconclusive, it is speculated that the term "uniform" arose from the concept of equiprobability in dice games (note that the dice games would have discrete and not continuous uniform sample space). Equiprobability was mentioned in Gerolamo Cardano's Liber de Ludo Aleae, a manual written in 16th century and detailed on advanced probability calculus in relation to dice.[12]
Remove ads
See also
- Discrete uniform distribution
- Beta distribution
- Box–Muller transform
- Probability plot
- Q–Q plot
- Rectangular function
- Irwin–Hall distribution — In the degenerate case where n=1, the Irwin-Hall distribution generates a uniform distribution between 0 and 1.
- Bates distribution — Similar to the Irwin-Hall distribution, but rescaled for n. Like the Irwin-Hall distribution, in the degenerate case where n=1, the Bates distribution generates a uniform distribution between 0 and 1.
Remove ads
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



![{\displaystyle [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![{\displaystyle {\mathcal {U}}_{[a,b]}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/906b38f0905adef68e3c8c7ca6de15858f7742ce)

![{\displaystyle {\begin{cases}{\frac {1}{b-a}}&{\text{for }}x\in [a,b]\\0&{\text{otherwise}}\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/648692e002b720347c6c981aeec2a8cca7f4182f)
![{\displaystyle {\begin{cases}0&{\text{for }}x<a\\{\frac {x-a}{b-a}}&{\text{for }}x\in [a,b]\\1&{\text{for }}x>b\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2948c023c98e2478806980eb7f5a03810347a568)









![{\displaystyle f(x)={\begin{cases}{\dfrac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[8pt]0&{\text{for }}x<a\ {\text{ or }}\ x>b.\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fd04990d517bf9bb3663f31086a89abd1b0f077f)



![{\displaystyle [c,d],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a9d224646c92ef76fbe024ed2eb56cb2964cab95)










![{\displaystyle f(x)={\begin{cases}{\dfrac {1}{2\sigma {\sqrt {3}}}}&{\text{for }}-\sigma {\sqrt {3}}\leq x-\mu \leq \sigma {\sqrt {3}},\\[2pt]0&{\text{otherwise}}.\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/312995655df7721197b7772acbe6efb18cdf1056)
![{\displaystyle F(x)={\begin{cases}0&{\text{for }}x<a,\\[8pt]{\frac {x-a}{b-a}}&{\text{for }}a\leq x\leq b,\\[8pt]1&{\text{for }}x>b.\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/32f8fa14b36ce1147021a210b875bcc4b91d24a3)






![{\displaystyle [f(x){\text{ vs }}x],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d57d12780dd2f37ecebcef1541f0fdccf1d5358e)











![{\displaystyle M_{X}=\operatorname {E} \left[e^{tX}\right]=\int _{a}^{b}e^{tx}{\frac {dx}{b-a}}={\frac {e^{tb}-e^{ta}}{t(b-a)}}={\frac {B^{t}-A^{t}}{t(b-a)}},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6d264e19e2b684d2c7a50a7a74deec4f37522dd7)







![{\displaystyle f(x)={\begin{cases}{\frac {1}{2b}}&{\text{for }}-b\leq x\leq b,\\[8pt]0&{\text{otherwise}};\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/528f4cb42767408146084a01d1836f80926a6458)



![{\displaystyle [-{\tfrac {1}{2}},{\tfrac {1}{2}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6cb7c3f1928e147f684b9cba323e45f0840c4ef4)













![{\displaystyle \operatorname {E} [X]=\int _{a}^{b}x{\frac {dx}{b-a}}={\frac {b^{2}-a^{2}}{2(b-a)}}={\frac {b+a}{2}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/552174da28a027cf2c7b8eb9e43973604b3d6585)
![{\displaystyle \operatorname {E} \left[X^{2}\right]=\int _{a}^{b}x^{2}{\frac {dx}{b-a}}={\frac {b^{3}-a^{3}}{3(b-a)}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e547791a2f771063976b3f5535122d096a0028e4)
![{\displaystyle \operatorname {E} \left[X^{n}\right]=\int _{a}^{b}x^{n}{\frac {dx}{b-a}}={\frac {b^{n+1}-a^{n+1}}{(n+1)(b-a)}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/03156c02c5f1de0f60aab478ff47e2649f4e1c35)
![{\displaystyle \operatorname {Var} [X]=\operatorname {E} \left[{\left(X-\operatorname {E} [X]\right)}^{2}\right]=\int _{a}^{b}\left(x-{\frac {a+b}{2}}\right)^{2}{\frac {dx}{b-a}}={\frac {(b-a)^{2}}{12}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/112a80de66789bf7cb497108fff7082e54c3dd96)




![{\displaystyle \operatorname {E} \left[X_{(k)}\right]={\frac {k}{n+1}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8688b18b2d8a32b8503ea2ab8da87b1b907407e5)
![{\displaystyle \operatorname {Var} \left[X_{(k)}\right]={\frac {k(n-k+1)}{(n+1)^{2}(n+2)}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d03c3ea205715beaba2fa8a32fea43f189c1013c)


![{\displaystyle [x,x+\ell ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/884130fbd3c593f4108f325e7ce5f5724e808872)

![{\displaystyle \Pr {\big (}X\in [x,x+\ell ]{\big )}=\int _{x}^{x+\ell }{\frac {dy}{b-a}}={\frac {\ell }{b-a}},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4b4a2d74fbb4a3b7148058cb6222a72fe58b83f2)






![{\displaystyle [0,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ba22e25e8f8604f012c599a7d4962562c4bb3f02)









![{\displaystyle U_{[0,L]},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0e995684064674d2d06963db2a581277bfa0c0e6)



![{\displaystyle f(t)=n{\frac {1}{L}}\left({\frac {t}{L}}\right)^{n-1}\!=n{\frac {t^{n-1}}{L^{n}}}1\!\!1_{[0,L]}(t),}](http://wikimedia.org/api/rest_v1/media/math/render/svg/55bb994d51861c2c29398652df1cf3c2b79caf0a)
![{\displaystyle 1\!\!1_{[0,L]}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/79cff43b95a58c16bc9a5d97be265cabd4a635bb)
![{\displaystyle [0,L].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/865dd4a189168d3c11e65b12bbb7880568652e1f)
![{\displaystyle \Pr {\big (}[{\hat {\theta }},{\hat {\theta }}+\varepsilon ]\ni \theta {\big )}\geq 1-\alpha }](http://wikimedia.org/api/rest_v1/media/math/render/svg/551b3f94638b0326d17c9d4dca7536f6ceeb3826)


![{\displaystyle \Pr {\big (}[{\hat {\theta }},{\hat {\theta }}(1+\varepsilon )]\ni \theta {\big )}\geq 1-\alpha }](http://wikimedia.org/api/rest_v1/media/math/render/svg/76d99f8778c0be6fce3a7ac95c58b20b2f1a9c0d)




