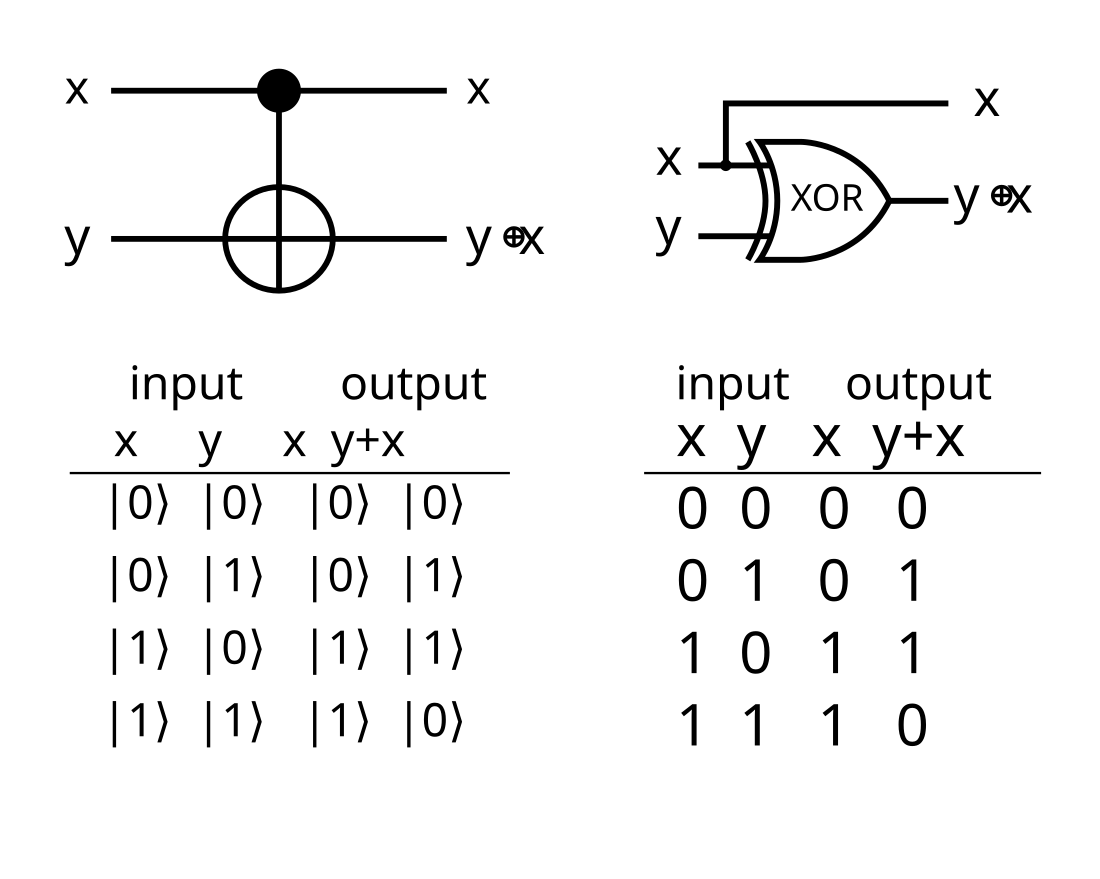
Controlled NOT gate

In computer science, the controlled NOT gate (also C-NOT or CNOT), controlled-X gate, controlled-bit-flip gate, Feynman gate or controlled Pauli-X is a quantum logic gate that is an essential component in the construction of a gate-based quantum computer. It can be used to entangle and disentangle Bell states. Any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit rotations.[1][2] The gate is sometimes named after Richard Feynman who developed an early notation for quantum gate diagrams in 1986.[3][4][5]

The CNOT can be expressed in the Pauli basis as:

${\displaystyle {\mbox{CNOT}}=e^{i{\frac {\pi }{4}}(I-Z_{1})(I-X_{2})}=e^{-i{\frac {\pi }{4}}(I-Z_{1})(I-X_{2})}.}$

Being both unitary and Hermitian, CNOT has the property ${\displaystyle e^{i\theta U}=(\cos \theta )I+(i\sin \theta )U}$ and ${\displaystyle U=e^{i{\frac {\pi }{2}}(I-U)}=e^{-i{\frac {\pi }{2}}(I-U)}}$, and is involutory.

The CNOT gate can be further decomposed as products of rotation operator gates and exactly one two qubit interaction gate, for example

${\displaystyle {\mbox{CNOT}}=e^{-i{\frac {\pi }{4}}}R_{y_{1}}(-\pi /2)R_{x_{1}}(-\pi /2)R_{x_{2}}(-\pi /2)R_{xx}(\pi /2)R_{y_{1}}(\pi /2).}$

In general, any single qubit unitary gate can be expressed as ${\displaystyle U=e^{iH}}$, where H is a Hermitian matrix, and then the controlled U is ${\displaystyle CU=e^{i{\frac {1}{2}}(I-Z_{1})H_{2}}}$.

The CNOT gate is also used in classical reversible computing.