
Rational number
Quotient of two integers / From Wikipedia, the free encyclopedia
Dear Wikiwand AI, let's keep it short by simply answering these key questions:
Can you list the top facts and stats about Rational number?
Summarize this article for a 10 year old
In mathematics, a rational number is a number that can be expressed as the quotient or fraction 



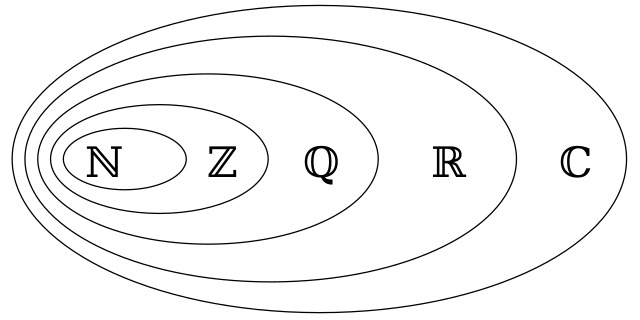
 are included in the real numbers
are included in the real numbers  , which are included in the complex numbers
, which are included in the complex numbers  , while rationals include the integers
, while rationals include the integers  , which in turn include the natural numbers
, which in turn include the natural numbers  .
.A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: 3/4 = 0.75), or eventually begins to repeat the same finite sequence of digits over and over (example: 9/44 = 0.20454545...).[4] This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see Repeating decimal § Extension to other bases).
A real number that is not rational is called irrational.[5] Irrational numbers include the square root of 2 (
Rational numbers can be formally defined as equivalence classes of pairs of integers (p, q) with q ≠ 0, using the equivalence relation defined as follows:
The fraction 
Rational numbers together with addition and multiplication form a field which contains the integers, and is contained in any field containing the integers. In other words, the field of rational numbers is a prime field, and a field has characteristic zero if and only if it contains the rational numbers as a subfield. Finite extensions of 

In mathematical analysis, the rational numbers form a dense subset of the real numbers. The real numbers can be constructed from the rational numbers by completion, using Cauchy sequences, Dedekind cuts, or infinite decimals (see Construction of the real numbers).
