Top Qs
Timeline
Chat
Perspective
Real number
Number representing a continuous quantity From Wikipedia, the free encyclopedia
Remove ads
In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a duration or temperature. Here, continuous means that pairs of values can have arbitrarily small differences.[a] Every real number can be almost uniquely represented by an infinite decimal expansion.[b][1]
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (July 2024) |
The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives.[c]
The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold R, often using blackboard bold, .[2][3] The adjective real, used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of −1.[4]
The real numbers include the rational numbers, such as the integer −5 and the fraction 4 / 3. The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) are the root of a polynomial with integer coefficients, such as the square root √2 = 1.414...; these are called algebraic numbers. There are also real numbers which are not, such as π = 3.1415...; these are called transcendental numbers.[4]

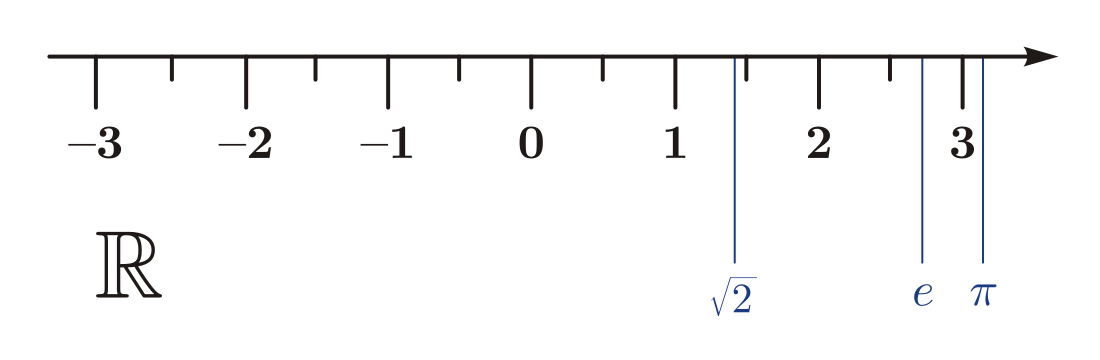
Real numbers can be thought of as all points on a line called the number line or real line, where the points corresponding to integers (..., −2, −1, 0, 1, 2, ...) are equally spaced.
The informal descriptions above of the real numbers are not sufficient for ensuring the correctness of proofs of theorems involving real numbers. The realization that a better definition was needed, and the elaboration of such a definition was a major development of 19th-century mathematics and is the foundation of real analysis, the study of real functions and real-valued sequences. A current axiomatic definition is that real numbers form the unique (up to an isomorphism) Dedekind-complete ordered field.[d] Other common definitions of real numbers include equivalence classes of Cauchy sequences (of rational numbers), Dedekind cuts, and infinite decimal representations. All these definitions satisfy the axiomatic definition and are thus equivalent.
Remove ads
Characterizing properties
Real numbers are completely characterized by their fundamental properties that can be summarized by saying that they form an ordered field that is Dedekind complete. Here, "completely characterized" means that there is a unique isomorphism between any two Dedekind complete ordered fields, and thus that their elements have exactly the same properties. This implies that one can manipulate real numbers and compute with them, without knowing how they can be defined; this is what mathematicians and physicists did during several centuries before the first formal definitions were provided in the second half of the 19th century. See Construction of the real numbers for details about these formal definitions and the proof of their equivalence.
Remove ads
Arithmetic
Summarize
Perspective
The real numbers form an ordered field. Intuitively, this means that methods and rules of elementary arithmetic apply to them. More precisely, there are two binary operations, addition and multiplication, and a total order that have the following properties.
- The addition of two real numbers a and b produce a real number denoted which is the sum of a and b.
- The multiplication of two real numbers a and b produce a real number denoted or which is the product of a and b.
- Addition and multiplication are both commutative, which means that and for every real numbers a and b.
- Addition and multiplication are both associative, which means that and for every real numbers a, b and c, and that parentheses may be omitted in both cases.
- Multiplication is distributive over addition, which means that for every real numbers a, b and c.
- There is a real number called zero and denoted 0 which is an additive identity, which means that for every real number a.
- There is a real number denoted 1 which is a multiplicative identity, which means that for every real number a.
- Every real number a has an additive inverse denoted This means that for every real number a.
- Every nonzero real number a has a multiplicative inverse denoted or This means that for every nonzero real number a.
- The total order is denoted being that it is a total order means two properties: given two real numbers a and b, exactly one of or is true; and if and then one has also
- The order is compatible with addition and multiplication, which means that implies for every real number c, and is implied by and
Many other properties can be deduced from the above ones. In particular:
- for every real number a
- for every nonzero real number a
Auxiliary operations
Several other operations are commonly used, which can be deduced from the above ones.
- Subtraction: the subtraction of two real numbers a and b results in the sum of a and the additive inverse −b of b; that is,
- Division: the division of a real number a by a nonzero real number b is denoted or and defined as the multiplication of a with the multiplicative inverse of b; that is,
- Absolute value: the absolute value of a real number a, denoted measures its distance from zero, and is defined as
Auxiliary order relations
The total order that is considered above is denoted and read as "a is less than b". Three other order relations are also commonly used:
- Greater than: read as "a is greater than b", is defined as if and only if
- Less than or equal to: read as "a is less than or equal to b" or "a is not greater than b", is defined as or equivalently as
- Greater than or equal to: read as "a is greater than or equal to b" or "a is not less than b", is defined as or equivalently as
Integers and fractions as real numbers
The real numbers 0 and 1 are commonly identified with the natural numbers 0 and 1. This allows identifying any natural number n with the sum of n real numbers equal to 1.
This identification can be pursued by identifying a negative integer (where is a natural number) with the additive inverse of the real number identified with Similarly a rational number (where p and q are integers and ) is identified with the division of the real numbers identified with p and q.
These identifications make the set of the rational numbers an ordered subfield of the real numbers The Dedekind completeness described below implies that some real numbers, such as are not rational numbers; they are called irrational numbers.
The above identifications make sense, since natural numbers, integers and real numbers are generally not defined by their individual nature, but by defining properties (axioms). So, the identification of natural numbers with some real numbers is justified by the fact that Peano axioms are satisfied by these real numbers, with the addition with 1 taken as the successor function.
Formally, one has an injective homomorphism of ordered monoids from the natural numbers to the integers an injective homomorphism of ordered rings from to the rational numbers and an injective homomorphism of ordered fields from to the real numbers The identifications consist of not distinguishing the source and the image of each injective homomorphism, and thus to write
These identifications are formally abuses of notation (since, formally, a rational number is an equivalence class of pairs of integers, and a real number is an equivalence class of Cauchy series), and are generally harmless. It is only in very specific situations, that one must avoid them and replace them by using explicitly the above homomorphisms. This is the case in constructive mathematics and computer programming. In the latter case, these homomorphisms are interpreted as type conversions that can often be done automatically by the compiler.
Remove ads
Dedekind completeness
Summarize
Perspective
Previous properties do not distinguish real numbers from rational numbers. This distinction is provided by Dedekind completeness, which states that every set of real numbers with an upper bound admits a least upper bound. This means the following. A set of real numbers is bounded above if there is a real number such that for all ; such a is called an upper bound of So, Dedekind completeness means that, if S is bounded above, it has an upper bound that is less than any other upper bound.
Dedekind completeness implies other sorts of completeness (see below), but also has some important consequences.
- Archimedean property: for every real number x, there is an integer n such that (take, where is the least upper bound of the integers less than x).
- Equivalently, if x is a positive real number, there is a positive integer n such that .
- Every positive real number x has a positive square root, that is, there exist a positive real number such that
- Every univariate polynomial of odd degree with real coefficients has at least one real root (if the leading coefficient is positive, take the least upper bound of real numbers for which the value of the polynomial is negative).
The last two properties are summarized by saying that the real numbers form a real closed field. This implies the real version of the fundamental theorem of algebra, namely that every polynomial with real coefficients can be factored into polynomials with real coefficients of degree at most two.
Remove ads
Decimal representation
Summarize
Perspective
The most common way of describing a real number is via its decimal representation, a sequence of decimal digits each representing the product of an integer between zero and nine times a power of ten, extending to finitely many positive powers of ten to the left and infinitely many negative powers of ten to the right. For a number x whose decimal representation extends k places to the left, the standard notation is the juxtaposition of the digits in descending order by power of ten, with non-negative and negative powers of ten separated by a decimal point, representing the infinite series
For example, for the circle constant k is zero and etc.
More formally, a decimal representation for a nonnegative real number x consists of a nonnegative integer k and integers between zero and nine in the infinite sequence
(If then by convention )
Such a decimal representation specifies the real number as the least upper bound of the decimal fractions that are obtained by truncating the sequence: given a positive integer n, the truncation of the sequence at the place n is the finite partial sum
The real number x defined by the sequence is the least upper bound of the which exists by Dedekind completeness.
Conversely, given a nonnegative real number x, one can define a decimal representation of x by induction, as follows. Define as decimal representation of the largest integer such that (this integer exists because of the Archimedean property). Then, supposing by induction that the decimal fraction has been defined for one defines as the largest digit such that and one sets
One can use the defining properties of the real numbers to show that x is the least upper bound of the So, the resulting sequence of digits is called a decimal representation of x.
Another decimal representation can be obtained by replacing with in the preceding construction. These two representations are identical, unless x is a decimal fraction of the form In this case, in the first decimal representation, all are zero for and, in the second representation, all 9. (see 0.999... for details).
In summary, there is a bijection between the real numbers and the decimal representations that do not end with infinitely many trailing 9.
The preceding considerations apply directly for every numeral base simply by replacing 10 with and 9 with
Remove ads
Topological completeness
Summarize
Perspective
A main reason for using real numbers is so that many sequences have limits. More formally, the reals are complete (in the sense of metric spaces or uniform spaces, which is a different sense than the Dedekind completeness of the order in the previous section):
A sequence (xn) of real numbers is called a Cauchy sequence if for any ε > 0 there exists an integer N (possibly depending on ε) such that the distance |xn − xm| is less than ε for all n and m that are both greater than N. This definition, originally provided by Cauchy, formalizes the fact that the xn eventually come and remain arbitrarily close to each other.
A sequence (xn) converges to the limit x if its elements eventually come and remain arbitrarily close to x, that is, if for any ε > 0 there exists an integer N (possibly depending on ε) such that the distance |xn − x| is less than ε for n greater than N.
Every convergent sequence is a Cauchy sequence, and the converse is true for real numbers, and this means that the topological space of the real numbers is complete.
The set of rational numbers is not complete. For example, the sequence (1; 1.4; 1.41; 1.414; 1.4142; 1.41421; ...), where each term adds a digit of the decimal expansion of the positive square root of 2, is Cauchy but it does not converge to a rational number (in the real numbers, in contrast, it converges to the positive square root of 2).
The completeness property of the reals is the basis on which calculus, and more generally mathematical analysis, are built. In particular, the test that a sequence is a Cauchy sequence allows proving that a sequence has a limit, without computing it, and even without knowing it.
For example, the standard series of the exponential function
converges to a real number for every x, because the sums
can be made arbitrarily small (independently of M) by choosing N sufficiently large. This proves that the sequence is Cauchy, and thus converges, showing that is well defined for every x.
"The complete ordered field"
The real numbers are often described as "the complete ordered field", a phrase that can be interpreted in several ways.
First, an order can be lattice-complete. It is easy to see that no ordered field can be lattice-complete, because it can have no largest element (given any element z, z + 1 is larger).
Additionally, an order can be Dedekind-complete, see § Axiomatic approach. The uniqueness result at the end of that section justifies using the word "the" in the phrase "complete ordered field" when this is the sense of "complete" that is meant. This sense of completeness is most closely related to the construction of the reals from Dedekind cuts, since that construction starts from an ordered field (the rationals) and then forms the Dedekind-completion of it in a standard way.
These two notions of completeness ignore the field structure. However, an ordered group (in this case, the additive group of the field) defines a uniform structure, and uniform structures have a notion of completeness; the description in § Completeness is a special case. (We refer to the notion of completeness in uniform spaces rather than the related and better known notion for metric spaces, since the definition of metric space relies on already having a characterization of the real numbers.) It is not true that is the only uniformly complete ordered field, but it is the only uniformly complete Archimedean field, and indeed one often hears the phrase "complete Archimedean field" instead of "complete ordered field". Every uniformly complete Archimedean field must also be Dedekind-complete (and vice versa), justifying using "the" in the phrase "the complete Archimedean field". This sense of completeness is most closely related to the construction of the reals from Cauchy sequences (the construction carried out in full in this article), since it starts with an Archimedean field (the rationals) and forms the uniform completion of it in a standard way.
But the original use of the phrase "complete Archimedean field" was by David Hilbert, who meant still something else by it. He meant that the real numbers form the largest Archimedean field in the sense that every other Archimedean field is a subfield of . Thus is "complete" in the sense that nothing further can be added to it without making it no longer an Archimedean field. This sense of completeness is most closely related to the construction of the reals from surreal numbers, since that construction starts with a proper class that contains every ordered field (the surreals) and then selects from it the largest Archimedean subfield.
Remove ads
Cardinality
The set of all real numbers is uncountable, in the sense that while both the set of all natural numbers {1, 2, 3, 4, ...} and the set of all real numbers are infinite sets, there exists no one-to-one function from the real numbers to the natural numbers. The cardinality of the set of all real numbers is called the cardinality of the continuum and commonly denoted by It is strictly greater than the cardinality of the set of all natural numbers, denoted and called Aleph-zero or aleph-nought. The cardinality of the continuum equals the cardinality of the power set of the natural numbers, that is, the set of all subsets of the natural numbers.
The statement that there is no cardinality strictly greater than and strictly smaller than is known as the continuum hypothesis (CH). It is neither provable nor refutable using the axioms of Zermelo–Fraenkel set theory including the axiom of choice (ZFC)—the standard foundation of modern mathematics. In fact, some models of ZFC satisfy CH, while others violate it.[5]
Remove ads
Other properties
Summarize
Perspective
As a topological space, the real numbers are separable. This is because the set of rationals, which is countable, is dense in the real numbers. The irrational numbers are also dense in the real numbers, however they are uncountable and have the same cardinality as the reals.
The real numbers form a metric space: the distance between x and y is defined as the absolute value |x − y|. By virtue of being a totally ordered set, they also carry an order topology; the topology arising from the metric and the one arising from the order are identical, but yield different presentations for the topology—in the order topology as ordered intervals, in the metric topology as epsilon-balls. The Dedekind cuts construction uses the order topology presentation, while the Cauchy sequences construction uses the metric topology presentation. The reals form a contractible (hence connected and simply connected), separable and complete metric space of Hausdorff dimension 1. The real numbers are locally compact but not compact. There are various properties that uniquely specify them; for instance, all unbounded, connected, and separable order topologies are necessarily homeomorphic to the reals.
Every nonnegative real number has a square root in , although no negative number does. This shows that the order on is determined by its algebraic structure. Also, every polynomial of odd degree admits at least one real root: these two properties make the premier example of a real closed field. Proving this is the first half of one proof of the fundamental theorem of algebra.
The reals carry a canonical measure, the Lebesgue measure, which is the Haar measure on their structure as a topological group normalized such that the unit interval [0;1] has measure 1. There exist sets of real numbers that are not Lebesgue measurable, e.g. Vitali sets.
The supremum axiom of the reals refers to subsets of the reals and is therefore a second-order logical statement. It is not possible to characterize the reals with first-order logic alone: the Löwenheim–Skolem theorem implies that there exists a countable dense subset of the real numbers satisfying exactly the same sentences in first-order logic as the real numbers themselves. The set of hyperreal numbers satisfies the same first order sentences as . Ordered fields that satisfy the same first-order sentences as are called nonstandard models of . This is what makes nonstandard analysis work; by proving a first-order statement in some nonstandard model (which may be easier than proving it in ), we know that the same statement must also be true of .
The field of real numbers is an extension field of the field of rational numbers, and can therefore be seen as a vector space over . Zermelo–Fraenkel set theory with the axiom of choice guarantees the existence of a basis of this vector space: there exists a set B of real numbers such that every real number can be written uniquely as a finite linear combination of elements of this set, using rational coefficients only, and such that no element of B is a rational linear combination of the others. However, this existence theorem is purely theoretical, as such a base has never been explicitly described.
The well-ordering theorem implies that the real numbers can be well-ordered if the axiom of choice is assumed: there exists a total order on with the property that every nonempty subset of has a least element in this ordering. (The standard ordering ≤ of the real numbers is not a well-ordering since e.g. an open interval does not contain a least element in this ordering.) Again, the existence of such a well-ordering is purely theoretical, as it has not been explicitly described. If V=L is assumed in addition to the axioms of ZF, a well ordering of the real numbers can be shown to be explicitly definable by a formula.[6]
A real number may be either computable or uncomputable; either algorithmically random or not; and either arithmetically random or not.
Remove ads
History
Summarize
Perspective

Simple fractions were used by the Egyptians around 1000 BC; the Vedic "Shulba Sutras" ("The rules of chords") in c. 600 BC include what may be the first "use" of irrational numbers. The concept of irrationality was implicitly accepted by early Indian mathematicians such as Manava (c. 750–690 BC), who was aware that the square roots of certain numbers, such as 2 and 61, could not be exactly determined.[7]
Around 500 BC, the Greek mathematicians led by Pythagoras also realized that the square root of 2 is irrational.
For Greek mathematicians, numbers were only the natural numbers. Real numbers were called "proportions", being the ratios of two lengths, or equivalently being measures of a length in terms of another length, called unit length. Two lengths are "commensurable", if there is a unit in which they are both measured by integers, that is, in modern terminology, if their ratio is a rational number. Eudoxus of Cnidus (c. 390−340 BC) provided a definition of the equality of two irrational proportions in a way that is similar to Dedekind cuts (introduced more than 2,000 years later), except that he did not use any arithmetic operation other than multiplication of a length by a natural number (see Eudoxus of Cnidus). This may be viewed as the first definition of the real numbers.
The Middle Ages brought about the acceptance of zero, negative numbers, integers, and fractional numbers, first by Indian and Chinese mathematicians, and then by Arabic mathematicians, who were also the first to treat irrational numbers as algebraic objects (the latter being made possible by the development of algebra).[8] Arabic mathematicians merged the concepts of "number" and "magnitude" into a more general idea of real numbers.[9] The Egyptian mathematician Abū Kāmil Shujā ibn Aslam (c. 850–930) was the first to accept irrational numbers as solutions to quadratic equations, or as coefficients in an equation (often in the form of square roots, cube roots, and fourth roots).[10] In Europe, such numbers, not commensurable with the numerical unit, were called irrational or surd ("deaf").
In the 16th century, Simon Stevin created the basis for modern decimal notation, and insisted that there is no difference between rational and irrational numbers in this regard.
In the 17th century, Descartes introduced the term "real" to describe roots of a polynomial, distinguishing them from "imaginary" numbers.
In the 18th and 19th centuries, there was much work on irrational and transcendental numbers. Lambert (1761) gave a flawed proof that π cannot be rational; Legendre (1794) completed the proof[11] and showed that π is not the square root of a rational number.[12] Liouville (1840) showed that neither e nor e2 can be a root of an integer quadratic equation, and then established the existence of transcendental numbers; Cantor (1873) extended and greatly simplified this proof.[13] Hermite (1873) proved that e is transcendental, and Lindemann (1882), showed that π is transcendental. Lindemann's proof was much simplified by Weierstrass (1885), Hilbert (1893), Hurwitz,[14] and Gordan.[15]
The concept that many points existed between rational numbers, such as the square root of 2, was well known to the ancient Greeks. The existence of a continuous number line was considered self-evident, but the nature of this continuity, presently called completeness, was not understood. The rigor developed for geometry did not cross over to the concept of numbers until the 1800s.[16]
Modern analysis
The developers of calculus used real numbers and limits without defining them rigorously. In his Cours d'Analyse (1821), Cauchy made calculus rigorous, but he used the real numbers without defining them, and assumed without proof that every Cauchy sequence has a limit and that this limit is a real number.
In 1854 Bernhard Riemann highlighted the limitations of calculus in the method of Fourier series, showing the need for a rigorous definition of the real numbers.[17]: 672
Beginning with Richard Dedekind in 1858, several mathematicians worked on the definition of the real numbers, including Hermann Hankel, Charles Méray, and Eduard Heine, leading to the publication in 1872 of two independent definitions of real numbers, one by Dedekind, as Dedekind cuts, and the other one by Georg Cantor, as equivalence classes of Cauchy sequences.[18] Several problems were left open by these definitions, which contributed to the foundational crisis of mathematics. Firstly both definitions suppose that rational numbers and thus natural numbers are rigorously defined; this was done a few years later with Peano axioms. Secondly, both definitions involve infinite sets (Dedekind cuts and sets of the elements of a Cauchy sequence), and Cantor's set theory was published several years later. Thirdly, these definitions imply quantification on infinite sets, and this cannot be formalized in the classical logic of first-order predicates. This is one of the reasons for which higher-order logics were developed in the first half of the 20th century.
In 1874 Cantor showed that the set of all real numbers is uncountably infinite, but the set of all algebraic numbers is countably infinite. Cantor's first uncountability proof was different from his famous diagonal argument published in 1891.
Remove ads
Formal definitions
Summarize
Perspective
The real number system can be defined axiomatically up to an isomorphism, which is described hereinafter. There are also many ways to construct "the" real number system, and a popular approach involves starting from natural numbers, then defining rational numbers algebraically, and finally defining real numbers as equivalence classes of their Cauchy sequences or as Dedekind cuts, which are certain subsets of rational numbers.[19] Another approach is to start from some rigorous axiomatization of Euclidean geometry (say of Hilbert or of Tarski), and then define the real number system geometrically. All these constructions of the real numbers have been shown to be equivalent, in the sense that the resulting number systems are isomorphic.
Axiomatic approach
Let denote the set of all real numbers. Then:
- The set is a field, meaning that addition and multiplication are defined and have the usual properties.
- The field is ordered, meaning that there is a total order ≥ such that for all real numbers x, y and z:
- if x ≥ y, then x + z ≥ y + z;
- if x ≥ 0 and y ≥ 0, then xy ≥ 0.
- The order is Dedekind-complete, meaning that every nonempty subset S of with an upper bound in has a least upper bound (a.k.a., supremum) in .
The last property applies to the real numbers but not to the rational numbers (or to other more exotic ordered fields). For example, has a rational upper bound (e.g., 1.42), but no least rational upper bound, because is not rational.
These properties imply the Archimedean property (which is not implied by other definitions of completeness), which states that the set of integers has no upper bound in the reals. In fact, if this were false, then the integers would have a least upper bound N; then, N – 1 would not be an upper bound, and there would be an integer n such that n > N – 1, and thus n + 1 > N, which is a contradiction with the upper-bound property of N.
The real numbers are uniquely specified by the above properties. More precisely, given any two Dedekind-complete ordered fields and , there exists a unique field isomorphism from to . This uniqueness allows us to think of them as essentially the same mathematical object.
For another axiomatization of see Tarski's axiomatization of the reals.
Construction from the rational numbers
The real numbers can be constructed as a completion of the rational numbers, in such a way that a sequence defined by a decimal or binary expansion like (3; 3.1; 3.14; 3.141; 3.1415; ...) converges to a unique real number—in this case π. For details and other constructions of real numbers, see Construction of the real numbers.
Remove ads
Applications and connections
Summarize
Perspective
Physics
In the physical sciences most physical constants, such as the universal gravitational constant, and physical variables, such as position, mass, speed, and electric charge, are modeled using real numbers. In fact the fundamental physical theories such as classical mechanics, electromagnetism, quantum mechanics, general relativity, and the standard model are described using mathematical structures, typically smooth manifolds or Hilbert spaces, that are based on the real numbers, although actual measurements of physical quantities are of finite accuracy and precision.
Physicists have occasionally suggested that a more fundamental theory would replace the real numbers with quantities that do not form a continuum, but such proposals remain speculative.[20]
Logic
The real numbers are most often formalized using the Zermelo–Fraenkel axiomatization of set theory, but some mathematicians study the real numbers with other logical foundations of mathematics. In particular, the real numbers are also studied in reverse mathematics and in constructive mathematics.[21]
The hyperreal numbers as developed by Edwin Hewitt, Abraham Robinson, and others extend the set of the real numbers by introducing infinitesimal and infinite numbers, allowing for building infinitesimal calculus in a way closer to the original intuitions of Leibniz, Euler, Cauchy, and others.
Edward Nelson's internal set theory enriches the Zermelo–Fraenkel set theory syntactically by introducing a unary predicate "standard". In this approach, infinitesimals are (non-"standard") elements of the set of the real numbers (rather than being elements of an extension thereof, as in Robinson's theory).
The continuum hypothesis posits that the cardinality of the set of the real numbers is ; i.e. the smallest infinite cardinal number after , the cardinality of the integers. Paul Cohen proved in 1963 that it is an axiom independent of the other axioms of set theory; that is: one may choose either the continuum hypothesis or its negation as an axiom of set theory, without contradiction.
Computation
Electronic calculators and computers cannot operate on arbitrary real numbers, because finite computers cannot directly store infinitely many digits or other infinite representations. Nor do they usually even operate on arbitrary definable real numbers, which are inconvenient to manipulate.
Instead, computers typically work with finite-precision approximations called floating-point numbers, a representation similar to scientific notation. The achievable precision is limited by the data storage space allocated for each number, whether as fixed-point, floating-point, or arbitrary-precision numbers, or some other representation. Most scientific computation uses binary floating-point arithmetic, often a 64-bit representation with around 16 decimal digits of precision. Real numbers satisfy the usual rules of arithmetic, but floating-point numbers do not. The field of numerical analysis studies the stability and accuracy of numerical algorithms implemented with approximate arithmetic.
Alternately, computer algebra systems can operate on irrational quantities exactly by manipulating symbolic formulas for them (such as or ) rather than their rational or decimal approximation.[22] But exact and symbolic arithmetic also have limitations: for instance, they are computationally more expensive; it is not in general possible to determine whether two symbolic expressions are equal (the constant problem); and arithmetic operations can cause exponential explosion in the size of representation of a single number (for instance, squaring a rational number roughly doubles the number of digits in its numerator and denominator, and squaring a polynomial roughly doubles its number of terms), overwhelming finite computer storage.[23]
A real number is called computable if there exists an algorithm that yields its digits. Because there are only countably many algorithms,[24] but an uncountable number of reals, almost all real numbers fail to be computable. Moreover, the equality of two computable numbers is an undecidable problem. Some constructivists accept the existence of only those reals that are computable. The set of definable numbers is broader, but still only countable.
Set theory
In set theory, specifically descriptive set theory, the Baire space is used as a surrogate for the real numbers since the latter have some topological properties (connectedness) that are a technical inconvenience. Elements of Baire space are referred to as "reals".
Remove ads
Vocabulary and notation
Summarize
Perspective
The set of all real numbers is denoted (blackboard bold) or R (upright bold). As it is naturally endowed with the structure of a field, the expression field of real numbers is frequently used when its algebraic properties are under consideration.
The sets of positive real numbers and negative real numbers are often noted and ,[25] respectively; and are also used.[26] The non-negative real numbers can be noted but one often sees this set noted [25] In French mathematics, the positive real numbers and negative real numbers commonly include zero, and these sets are noted respectively and [26] In this understanding, the respective sets without zero are called strictly positive real numbers and strictly negative real numbers, and are noted and [26]
The notation refers to the set of the n-tuples of elements of (real coordinate space), which can be identified to the Cartesian product of n copies of It is an n-dimensional vector space over the field of the real numbers, often called the coordinate space of dimension n; this space may be identified to the n-dimensional Euclidean space as soon as a Cartesian coordinate system has been chosen in the latter. In this identification, a point of the Euclidean space is identified with the tuple of its Cartesian coordinates.
In mathematics real is used as an adjective, meaning that the underlying field is the field of the real numbers (or the real field). For example, real matrix, real polynomial and real Lie algebra. The word is also used as a noun, meaning a real number (as in "the set of all reals").
Remove ads
Generalizations and extensions
Summarize
Perspective
The real numbers can be generalized and extended in several different directions:
- The complex numbers contain solutions to all polynomial equations and hence are an algebraically closed field unlike the real numbers. However, the complex numbers are not an ordered field.
- The affinely extended real number system adds two elements +∞ and −∞. It is a compact space. It is no longer a field, or even an additive group, but it still has a total order; moreover, it is a complete lattice.
- The real projective line adds only one value ∞. It is also a compact space. Again, it is no longer a field, or even an additive group. However, it allows division of a nonzero element by zero. It has cyclic order with topology described by point-pair separation.
- The long real line pastes together ℵ1* + ℵ1 copies of the real line plus a single point (here ℵ1* denotes the reversed ordering of ℵ1) to create an ordered set that is "locally" identical to the real numbers, but somehow longer; for instance, there is an order-preserving embedding of ℵ1 in the long real line but not in the real numbers. The long real line is the largest ordered set that is complete and locally Archimedean. As with the previous two examples, this set is no longer a field or additive group.
- Ordered fields extending the reals are the hyperreal numbers and the surreal numbers; both of them contain infinitesimal and infinitely large numbers and are therefore non-Archimedean ordered fields.
- Self-adjoint operators on a Hilbert space (for example, self-adjoint square complex matrices) generalize the reals in many respects: they can be ordered (though not totally ordered), they are complete, all their eigenvalues are real and they form a real associative algebra. Positive-definite operators correspond to the positive reals and normal operators correspond to the complex numbers.
See also
- Completeness of the real numbers
- Continued fraction
- Definable real numbers
- Positive real numbers
- Real analysis
Notes
- This is not sufficient for distinguishing the real numbers from the rational numbers; a property of completeness is also required.
- Rational numbers with a "terminating" decimal expansion have two decimal expansions (see 0.999...); the other real numbers have one decimal expansion.
- Limits and continuity can be defined in general topology without reference to real numbers, but these generalizations are relatively recent, and used only in very specific cases.
- More precisely, given two complete totally ordered fields, there is a unique isomorphism between them. This implies that the identity is the unique field automorphism of the reals that is compatible with the ordering. In fact, the identity is the unique field automorphism of the reals, since is equivalent to and the second formula is stable under field automorphisms.
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads