
Taxicab geometry
Type of metric geometry / From Wikipedia, the free encyclopedia
Dear Wikiwand AI, let's keep it short by simply answering these key questions:
Can you list the top facts and stats about Taxicab geometry?
Summarize this article for a 10 year old
Taxicab geometry or Manhattan geometry is geometry where the familiar Euclidean distance is ignored, and the distance between two points is instead defined to be the sum of the absolute differences of their respective Cartesian coordinates, a distance function (or metric) called the taxicab distance, Manhattan distance, or city block distance. The name refers to the island of Manhattan, or generically any planned city with a rectangular grid of streets, in which a taxicab can only travel along grid directions. In taxicab geometry, the distance between any two points equals the length of their shortest grid path. This different definition of distance also leads to a different definition of the length of a curve, for which a line segment between any two points has the same length as a grid path between those points rather than its Euclidean length.
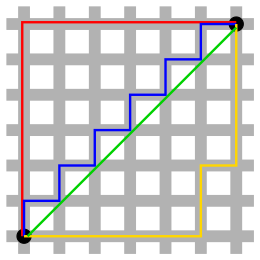
The taxicab distance is also sometimes known as rectilinear distance or L1 distance (see Lp space).[1] This geometry has been used in regression analysis since the 18th century, and is often referred to as LASSO. Its geometric interpretation dates to non-Euclidean geometry of the 19th century and is due to Hermann Minkowski.
In the two-dimensional real coordinate space 


