Weierstrass function

Not to be confused with the Weierstrass elliptic function (${\displaystyle \wp }$) or the Weierstrass sigma, zeta, or eta functions.

In mathematics, the Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function that is continuous everywhere but differentiable nowhere. It is also an example of a fractal curve.

Plot of Weierstrass function over the interval [−2, 2]. Like some other fractals, the function exhibits self-similarity: every zoom (red circle) is similar to the global plot.

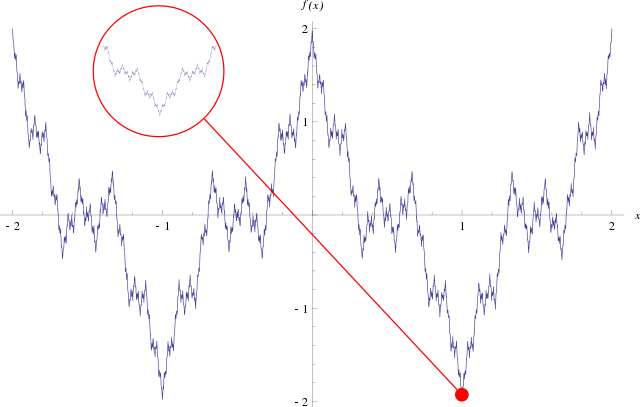
The Weierstrass function has been historically served the role of a pathological function, being the first published example (1872) specifically concocted to challenge the notion that every continuous function is differentiable except on a set of isolated points.^[1] Weierstrass's demonstration that continuity did not imply almost-everywhere differentiability upended mathematics, overturning several proofs that relied on geometric intuition and vague definitions of smoothness. These types of functions were denounced by contemporaries: Henri Poincaré famously described them as "monsters" and called Weierstrass' work "an outrage against common sense", while Charles Hermite wrote that they were a "lamentable scourge". The functions were difficult to visualize until the arrival of computers in the next century, and the results did not gain wide acceptance until practical applications such as models of Brownian motion necessitated infinitely jagged functions (nowadays known as fractal curves).^[2]

Construction

Animation based on the increasing of the b value from 0.1 to 5.

In Weierstrass's original paper, the function was defined as a Fourier series:

$${\displaystyle f(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x),}$$

where ${\textstyle 0<a<1}$, ${\textstyle b}$ is a positive odd integer, and

$${\displaystyle ab>1+{\frac {3}{2}}\pi .}$$

The minimum value of ${\textstyle b}$ for which there exists ${\textstyle 0<a<1}$ such that these constraints are satisfied is ${\textstyle b=7}$. This construction, along with the proof that the function is not differentiable over any interval, was first delivered by Weierstrass in a paper presented to the Königliche Akademie der Wissenschaften on 18 July 1872.^[3][4][5]

Despite being differentiable nowhere, the function is continuous: Since the terms of the infinite series which defines it are bounded by ${\textstyle \pm a^{n}}$ and this has finite sum for ${\textstyle 0<a<1}$, convergence of the sum of the terms is uniform by the Weierstrass M-test with ${\textstyle M_{n}=a^{n}}$. Since each partial sum is continuous, by the uniform limit theorem, it follows that ${\textstyle f}$ is continuous. Additionally, since each partial sum is uniformly continuous, it follows that ${\textstyle f}$ is also uniformly continuous.

It might be expected that a continuous function must have a derivative, or that the set of points where it is not differentiable should be countably infinite or finite. According to Weierstrass in his paper, earlier mathematicians including Gauss had often assumed that this was true. This might be because it is difficult to draw or visualise a continuous function whose set of nondifferentiable points is something other than a countable set of points. Analogous results for better behaved classes of continuous functions do exist, for example the Lipschitz functions, whose set of non-differentiability points must be a Lebesgue null set (Rademacher's theorem). When we try to draw a general continuous function, we usually draw the graph of a function which is Lipschitz or otherwise well-behaved. Moreover, the fact that the set of non-differentiability points for a monotone function is measure-zero implies that the rapid oscillations of Weierstrass' function are necessary to ensure that it is nowhere-differentiable.

The Weierstrass function was one of the first fractals studied, although this term was not used until much later. The function has detail at every level, so zooming in on a piece of the curve does not show it getting progressively closer and closer to a straight line. Rather between any two points no matter how close, the function will not be monotone.

The computation of the Hausdorff dimension ${\textstyle D}$ of the graph of the classical Weierstrass function was an open problem until 2018, while it was generally believed that ${\textstyle D=2+\log _{b}(a)<2}$.^[6][7] That D is strictly less than 2 follows from the conditions on ${\textstyle a}$ and ${\textstyle b}$ from above. Only after more than 30 years was this proved rigorously.^[8]

The term Weierstrass function is often used in real analysis to refer to any function with similar properties and construction to Weierstrass's original example. For example, the cosine function can be replaced in the infinite series by a piecewise linear "zigzag" function. G. H. Hardy showed that the function of the above construction is nowhere differentiable with the assumptions ${\textstyle 0<a<1,ab\geq 1}$.^[9]

Riemann function

The Weierstrass function is based on the earlier Riemann function, claimed to be differentiable nowhere. Occasionally, this function has also been called the Weierstrass function.^[10]

$${\displaystyle f(x)=\sum _{n=1}^{\infty }{\frac {\sin(n^{2}x)}{n^{2}}}}$$

While Bernhard Riemann strongly claimed that the function is differentiable nowhere, no evidence of this was published by Riemann, and Weierstrass noted that he did not find any evidence of it surviving either in Riemann's papers or orally from his students.

In 1916, G. H. Hardy confirmed that the function does not have a finite derivative in any value of ${\textstyle \pi x}$ where x is irrational or is rational with the form of either ${\textstyle {\frac {2A}{4B+1}}}$ or ${\textstyle {\frac {2A+1}{2B}}}$, where A and B are integers.^[9] In 1969, Joseph Gerver found that the Riemann function has a defined differential on every value of x that can be expressed in the form of ${\textstyle {\frac {2A+1}{2B+1}}\pi }$ with integer A and B, or rational multipliers of pi with an odd numerator and denominator. On these points, the function has a derivative of ${\textstyle -{\frac {1}{2}}}$.^[11] In 1971, J. Gerver showed that the function has no finite differential at the values of x that can be expressed in the form of ${\textstyle {\frac {2A}{2B+1}}\pi }$, completing the problem of the differentiability of the Riemann function.^[12]

As the Riemann function is differentiable only on a null set of points, it is differentiable almost nowhere.

Hölder continuity

It is convenient to write the Weierstrass function equivalently as

$${\displaystyle W_{\alpha }(x)=\sum _{n=0}^{\infty }b^{-n\alpha }\cos(b^{n}\pi x)}$$

for ${\textstyle \alpha =-{\frac {\ln(a)}{\ln(b)}}}$. Then ${\textstyle W_{\alpha }(x)}$ is Hölder continuous of exponent α, which is to say that there is a constant C such that

$${\displaystyle |W_{\alpha }(x)-W_{\alpha }(y)|\leq C|x-y|^{\alpha }}$$

for all ${\textstyle x}$ and ${\textstyle y}$.^[13] Moreover, ${\textstyle W_{1}}$ is Hölder continuous of all orders ${\textstyle \alpha <1}$ but not Lipschitz continuous.

Density of nowhere-differentiable functions

It turns out that the Weierstrass function is far from being an isolated example: although it is "pathological", it is also "typical" of continuous functions:

• In a topological sense: the set of nowhere-differentiable real-valued functions on [0, 1] is comeager in the vector space C([0, 1]; R) of all continuous real-valued functions on [0, 1] with the topology of uniform convergence.^[14][15]
• In a measure-theoretic sense: when the space C([0, 1]; R) is equipped with classical Wiener measure γ, the collection of functions that are differentiable at even a single point of [0, 1] has γ-measure zero. The same is true even if one takes finite-dimensional "slices" of C([0, 1]; R), in the sense that the nowhere-differentiable functions form a prevalent subset of C([0, 1]; R).

See also

• Blancmange curve
• Koch snowflake
• Nowhere continuous function

Notes

1. At least two researchers formulated continuous, nowhere differentiable functions before Weierstrass, but their findings were not published in their lifetimes. Around 1831, Bernard Bolzano (1781–1848), a Czech mathematician, philosopher, and Catholic priest, constructed such a function; however, it was not published until 1922. See:

   • Martin Jašek (1922) "Funkce Bolzanova" (Bolzano's function), Časopis pro Pěstování Matematiky a Fyziky (Journal for the Cultivation of Mathematics and Physics), vol. 51, no. 2, pages 69–76 (in Czech and German).
   • Vojtěch Jarník (1922) "O funkci Bolzanově" (On Bolzano's function), Časopis pro Pěstování Matematiky a Fyziky (Journal for the Cultivation of Mathematics and Physics), vol. 51, no. 4, pages 248 - 264 (in Czech). Available on-line in Czech at: http://dml.cz/bitstream/handle/10338.dmlcz/109021/CasPestMatFys_051-1922-4_5.pdf . Available on-line in English at: http://dml.cz/bitstream/handle/10338.dmlcz/400073/Bolzano_15-1981-1_6.pdf .
   • Karel Rychlík (1923) "Über eine Funktion aus Bolzanos handschriftlichem Nachlasse" (On a function from Bolzano's literary remains in manuscript), Sitzungsberichte der königlichen Böhmischen Gesellschaft der Wissenschaften (Prag) (Proceedings of the Royal Bohemian Society of Philosophy in Prague) (for the years 1921-1922), Class II, no. 4, pages 1-20. (Sitzungsberichte was continued as: Věstník Královské české společnosti nauk, třída matematicko-přírodovědecká (Journal of the Royal Czech Society of Science, Mathematics and Natural Sciences Class).)

   Around 1860, Charles Cellérier (1818 - 1889), a professor of mathematics, mechanics, astronomy, and physical geography at the University of Geneva, Switzerland, independently formulated a continuous, nowhere differentiable function that closely resembles Weierstrass's function. Cellérier's discovery was, however, published posthumously:

   • Cellérier, C. (1890) "Note sur les principes fondamentaux de l'analyse" (Note on the fundamental principles of analysis), Bulletin des sciences mathématiques, second series, vol. 14, pages 142 - 160.
2. Kucharski, Adam (26 October 2017). "Math's Beautiful Monsters: How a destructive idea paved the way for modern math". Retrieved 11 October 2023.
3. On page 560 of the 1872 Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin (Monthly Reports of the Royal Prussian Academy of Science in Berlin), there is a brief mention that on 18 July, "Hr. Weierstrass las über stetige Funktionen ohne bestimmte Differentialquotienten" (Mr. Weierstrass read [a paper] about continuous functions without definite [i.e., well-defined] derivatives [to members of the Academy]). However, Weierstrass's paper was not published in the Monatsberichte.
4. Karl Weierstrass, "Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen" [On continuous functions of a real argument which possess a definite derivative for no value of the argument], in: Königlich Preussichen Akademie der Wissenschaften, Mathematische Werke von Karl Weierstrass (Berlin, Germany: Mayer & Mueller, 1895), vol. 2, pages 71–74.
5. See also: Karl Weierstrass, Abhandlungen aus der Functionenlehre [Treatises from the Theory of Functions] (Berlin, Germany: Julius Springer, 1886), page 97.
6. Kenneth Falconer, The Geometry of Fractal Sets (Cambridge, England: Cambridge University Press, 1985), pages 114, 149.
7. See also: Brian R. Hunt (1998), "The Hausdorff dimension of graphs of Weierstrass functions", Proceedings of the American Mathematical Society, vol. 126, no. 3, pages 791–800.
8. Shen Weixiao (2018). "Hausdorff dimension of the graphs of the classical Weierstrass functions". Mathematische Zeitschrift. 289 (1–2): 223–266. arXiv:1505.03986. doi:10.1007/s00209-017-1949-1. ISSN 0025-5874. S2CID 118844077.
9. Hardy G. H. (1916) "Weierstrass's nondifferentiable function", Transactions of the American Mathematical Society, vol. 17, pages 301–325.
10. Weisstein, Eric W. "Weierstrass Function". MathWorld.
11. Gerver, Joseph (1969). "The Differentiability of the Riemann Function at Certain Rational Multiples of π". Proceedings of the National Academy of Sciences of the United States of America. 62 (3): 668–670. doi:10.1073/pnas.62.3.668. PMC 223649. PMID 16591735.
12. Gerver, Joseph (1971). "More on the Differentiability of the Riemann Function". American Journal of Mathematics. 93 (1): 33–41. doi:10.2307/2373445. JSTOR 2373445. S2CID 124562827.
13. Zygmund, A. (2002) [1935]. Trigonometric Series. Cambridge Mathematical Library. Vol. I, II (3rd ed.). Cambridge University Press. p. 47. ISBN 978-0-521-89053-3. MR 1963498.
14. Mazurkiewicz, S.. (1931). "Sur les fonctions non-dérivables". Studia Math. 3 (3): 92–94. doi:10.4064/sm-3-1-92-94.
15. Banach, S. (1931). "Über die Baire'sche Kategorie gewisser Funktionenmengen". Studia Math. 3 (3): 174–179. doi:10.4064/sm-3-1-174-179.

References

• David, Claire (2018), "Bypassing dynamical systems : A simple way to get the box-counting dimension of the graph of the Weierstrass function", Proceedings of the International Geometry Center, 11 (2), Academy of Sciences of Ukraine: 53–68, arXiv:1711.10349, doi:10.15673/tmgc.v11i2.1028
• Falconer, K. (1984), The Geometry of Fractal Sets, Cambridge Tracts in Mathematics, vol. Book 85, Cambridge: Cambridge University Press, ISBN 978-0-521-33705-2
• Gelbaum, B Bernard R.; Olmstead, John M. H. (2003) [1964], Counterexamples in Analysis, Dover Books on Mathematics, Dover Publications, ISBN 978-0-486-42875-8
• Hardy, G. H. (1916), "Weierstrass's nondifferentiable function" (PDF), Transactions of the American Mathematical Society, 17 (3), American Mathematical Society: 301–325, doi:10.2307/1989005, JSTOR 1989005
• Weierstrass, Karl (18 July 1872), Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen, Königlich Preussische Akademie der Wissenschaften
  • Weierstrass, Karl (1895), "Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen", Mathematische Werke von Karl Weierstrass, vol. 2, Berlin, Germany: Mayer & Müller, pp. 71–74
  • English translation: Edgar, Gerald A. (1993), "On continuous functions of a real argument that do not possess a well-defined derivative for any value of their argument", Classics on Fractals, Studies in Nonlinearity, Addison-Wesley Publishing Company, pp. 3–9, ISBN 978-0-201-58701-2

External links

• Weisstein, Eric W. "Weierstrass function". MathWorld. (a different Weierstrass Function which is also continuous and nowhere differentiable)
• Nowhere differentiable continuous function proof of existence using Banach's contraction principle.
• Nowhere monotonic continuous function proof of existence using the Baire category theorem.
• Johan Thim. "Continuous Nowhere Differentiable Functions". Master Thesis Lulea Univ of Technology 2003. Archived from the original on 22 February 2017. Retrieved 28 July 2006.
• Weierstrass function in the complex plane Archived 24 September 2009 at the Wayback Machine Beautiful fractal.
• SpringerLink - Journal of Fourier Analysis and Applications, Volume 16, Number 1 Simple Proofs of Nowhere-Differentiability for Weierstrass's Function and Cases of Slow Growth
• Weierstrass functions: continuous but not differentiable anywhere
• The Weierstrass Function by Brent Nelson at Berkeley, showing non differentiable