Cube

For other uses, see Cube (disambiguation).

A cube is a three-dimensional solid object in geometry. A cube has eight vertices and twelve straight edges of the same length, so that these edges form six square faces of the same size. It is an example of a polyhedron.

Cube
Type	Hanner polytope, orthogonal polyhedron, parallelohedron, Platonic solid, plesiohedron, regular polyhedron, zonohedron
Faces	6 square
Edges	12
Vertices	8
Euler char.	2
Vertex configuration	${\displaystyle 8\times (4^{3})}$
Schläfli symbol	${\displaystyle \{4,3\}}$
Symmetry group	octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$
Volume	side3
Dihedral angle (degrees)	90°
Dual polyhedron	regular octahedron
Properties	convex, edge-transitive, face-transitive, non-composite, orthogonal faces, Rupert property: can pass through a hole with its copy, vertex-transitive

The cube is found in many popular cultures, including toys and games, the arts, optical illusions, and architectural buildings. Cubes can be found in crystal structures, science, and technological devices. It is also found in ancient texts, such as Plato's work Timaeus, which described a set of solids now called Platonic solids, associating a cube with the classical element of earth. A cube with unit length is the canonical unit of volume in three-dimensional space, relative to which other solid objects are measured.

The cube relates to the construction of many polyhedra, such as truncation and attaching to other polyhedra. It also represents geometrical shapes. The cube can be attached to its faces with its copy to fill a space without leaving a gap, which forms a honeycomb.

The cube can be represented in many ways. One example is by drawing a graph, a structure in graph theory consisting of a set of vertices that are connected with an edge. This graph also represents the family of a cuboid, a polyhedron with six quadrilateral faces, which includes the cube as its special case. The cube and its graph are a three-dimensional hypercube, a family of polytopes that also includes the two-dimensional square and four-dimensional tesseract.

Properties

3D model of a cube

A cube is a polyhedron with eight vertices and twelve equal-length edges, forming six squares as its faces. A cube is a special case of a rectangular cuboid, which has six rectangular faces, each of which has a pair of opposite equal-length and parallel edges.^[1] Both polyhedra have the same dihedral angle, the angle between two adjacent faces at a common edge, a right angle or 90°, obtained from the interior angle (an angle formed between two adjacent sides at a common point of a polygon within) of a square.^[2][3] More generally, the cube and the rectangular cuboid are special cases of a cuboid, a polyhedron with six quadrilaterals (four-sided polygons).^[4] As for all convex polyhedra, the cube has Euler characteristic of 2, according to the formula ${\displaystyle V-E+F=2}$; the three letters denote respectively the number of vertices, edges, and faces.^[5]

All three square faces surrounding a vertex are orthogonal to each other, meaning the planes are perpendicular, forming a right angle between two adjacent squares. Hence, the cube is classified as an orthogonal polyhedron.^[6] The cube is a special case of other cuboids. These include a parallelepiped, a polyhedron with six parallelograms faces, because its pairs of opposite faces are congruent;^[7] a rhombohedron, as a special case of a parallelepiped with six rhombi faces, because the interior angle of all of the faces is right;^[8] and a trigonal trapezohedron, a polyhedron with congruent quadrilateral faces, since its square faces are the special cases of rhombi.^[9]

The cube is a non-composite or an elementary polyhedron. That is, no plane intersecting its surface only along edges, thereby cutting into two or more convex, regular-faced polyhedra.^[10]

Measurement

A face diagonal is denoted as ${\displaystyle AC}$ and a space diagonal is ${\displaystyle AC'}$

Given a cube with edge length ${\displaystyle a}$, the face diagonal of the cube is the diagonal of a square ${\displaystyle a{\sqrt {2}}}$, and the space diagonal of the cube is a line connecting two vertices that are not in the same face, formulated as ${\displaystyle a{\sqrt {3}}}$. Both formulas can be determined by using the Pythagorean theorem. The surface area of a cube ${\displaystyle A}$ is six times the area of a square:^[11] $${\displaystyle A=6a^{2}.}$$ The volume of a rectangular cuboid is the product of its length, width, and height. Because all the edges of a cube are equal in length, the formula for the volume of a cube is the third power of its side length.^[11] This leads to the use of the term cube as a verb, to mean raising any number to the third power:^[4] $${\displaystyle V=a^{3}.}$$

The cube has three types of closed geodesics, or paths on a cube's surface that are locally straight. In other words, they avoid the vertices, follow line segments across the faces that they cross, and form complementary angles on the two incident faces of each edge that they cross. One type lies in a plane parallel to any face of the cube, forming a square congruent to a face, four times the length of each edge. Another type lies in a plane perpendicular to the long diagonal, forming a regular hexagon; its length is ${\displaystyle 3{\sqrt {2}}}$ times that of an edge. The third type is a non-planar hexagon.^[12]

Insphere, midsphere, circumsphere

An insphere of a cube ${\displaystyle r_{i}}$ is a sphere tangent to the faces of a cube at their centroids. Its midsphere ${\displaystyle r_{m}}$ is a sphere tangent to the edges of a cube. Its circumsphere ${\displaystyle r_{c}}$ is a sphere tangent to the vertices of a cube. With edge length ${\displaystyle a}$, they are respectively:^[13] $${\displaystyle r_{i}={\frac {1}{2}}a=0.5a,\qquad r_{m}={\frac {\sqrt {2}}{2}}a\approx 0.707a,\qquad r_{c}={\frac {\sqrt {3}}{2}}a\approx 0.866a.}$$

Unit cube

Main articles: Unit cube, Prince Rupert's cube, and Doubling the cube

Prince Rupert's cube

A unit cube is a cube with 1 unit in length along each edge. It follows that each face is a unit square and that the entire figure has a volume of 1 cubic unit.^[14][15] Prince Rupert of the Rhine, known for Prince Rupert's drop, wagered whether a cube could be passed through a hole made in another cube of the same size. The story recounted in 1693 by English mathematician John Wallis answered that it is possible, although there were some errors in Wallis's presentation. Roughly a century later, Dutch mathematician Pieter Nieuwland provided a better solution that the edges of a cube passing through the unit cube's hole could be as large as approximately 1.06 units in length.^[16][17] One way to obtain this result is by using the Pythagorean theorem or the formula for Euclidean distance in three-dimensional space.^[18]

An ancient problem of doubling the cube requires the construction of a cube with a volume twice the original by using only a compass and straightedge. This was concluded by French mathematician Pierre Wantzel in 1837, proving that it is impossible to implement since a cube with twice the volume of the original—the cube root of 2, ${\displaystyle {\sqrt[{3}]{2}}}$—is not constructible.^[19] However, this problem was solved with folding an origami paper by Messer (1986).^[20]

Symmetry

The dual polyhedron of a cube is the regular octahedron. Both have octahedral symmetry.

The cube has octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$ of order 48. In other words, the cube has 48 isometries (including identity), each of which transforms the cube to itself. These transformations include nine reflection symmetries (where two halves cut by a plane are identical): three cut the cube at the midpoints of its edges, and six cut diagonally. The cube also has thirteen axes of rotational symmetry (whereby rotation around the axis results in an identical appearance): three axes pass through the centroids of opposite faces, six through the midpoints of opposite edges, and four through opposite vertices; these axes are respectively four-fold rotational symmetry (0°, 90°, 180°, and 270°), two-fold rotational symmetry (0° and 180°), and three-fold rotational symmetry (0°, 120°, and 240°).^{[21][22][23][24]}

The dual polyhedron can be obtained from each of the polyhedra's vertices tangent to a plane by a process known as polar reciprocation.^[25] One property of dual polyhedra is that the polyhedron and its dual share their three-dimensional symmetry point group. In this case, the dual polyhedron of a cube is the regular octahedron, and both of these polyhedra have the same octahedral symmetry.^[26]

The cube is face-transitive, meaning its two square faces are alike and can be mapped by rotation and reflection.^[27] It is vertex-transitive, meaning all of its vertices are equivalent and can be mapped isometrically under its symmetry.^[28] It is also edge-transitive, meaning the same kind of faces surround each of its vertices in the same or reverse order, and each pair of adjacent faces has the same dihedral angle. Therefore, the cube is a regular polyhedron.^[29] Each vertex is surrounded by three squares, so the cube is ${\displaystyle 4.4.4}$ by vertex configuration or ${\displaystyle \{4,3\}}$ by Schläfli symbol.^[30]

Appearances

In popular cultures

A six-sided die

A completed Skewb

The Alamo sculpture

Cubes have appeared in many roles in popular culture. It is the most common form of dice.^[27] Puzzle toys such as pieces of a Soma cube,^[31] Rubik's Cube, and Skewb are built of cubes.^[32] Minecraft is an example of a sandbox video game of cubic blocks.^[33] The outdoor sculpture Alamo (1967) is a cube that spins around its vertical axis.^[34] Optical illusions such as the impossible cube and Necker cube have been explored by artists such as M. C. Escher.^[35] The cube was applied in Alberti's treatise on Renaissance architecture, De re aedificatoria (1450).^[36] Cube houses in the Netherlands are a set of cubical houses whose hexagonal space diagonals become the main floor.^[37]

In nature and science

Simple cubic crystal structure

Table salt cubic crystals

Ball-and-stick model of cubane

Cubes are also found in various fields of natural science and technology. It is applied to the unit cell of a crystal known as a cubic crystal system.^[38] Table salt is an example of a mineral with a commonly cubic shape.^[39] Other examples are pyrite (although there are many variations)^[40] and uranium cubic-shaped in nuclear program.^[41] The radiolarian Lithocubus geometricus, discovered by Ernst Haeckel, has a cubic shape.^[42] Cubane is a synthetic hydrocarbon consisting of eight carbon atoms arranged at the corners of a cube, with one hydrogen atom attached to each carbon atom.^[43]

A historical attempt to unify three physics ideas of relativity, gravitation, and quantum mechanics used the framework of a cube known as a cGh cube.^[44]

The Norwegian CubeSat

Corner reflector redirecting two rays back to their source

Technological cubes include the spacecraft device CubeSat,^[45] thermal radiation demonstration device Leslie cube,^[46] and web server machine Cobalt Qube.^[47] Cubical grids are usual in three-dimensional Cartesian coordinate systems.^[48] In computer graphics, an algorithm divides the input volume into a discrete set of cubes known as the unit on isosurface,^[49] and the faces of a cube can be used for mapping a shape.^[50] In various areas of engineering, including traffic signs and radar, the corner of a cube is useful as a retroreflector, called a corner reflector, which redirects any ray or wave back to its source.^[51]

In antiquity

Further information: Platonic solids § History, and Mysterium Cosmographicum § Shapes and the planets

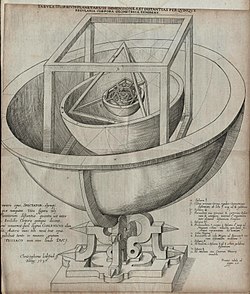
Sketch of a cube by Johannes Kepler

Kepler's Platonic solid model of the Solar System

The Platonic solids are five polyhedra known since antiquity. The set is named for Plato, who attributed these solids to nature in his dialogue Timaeus. One of them, the cube, represented the classical element of earth because of the building blocks of Earth's foundation.^[52] Euclid's Elements defined the Platonic solids, including the cube, and showed how to find the ratio of the circumscribed sphere's diameter to the edge length.^[53]

Following Plato's use of the regular polyhedra as symbols of nature, Johannes Kepler in his Harmonices Mundi sketched each of the Platonic solids; he decorated the cube's side with a tree.^[54] In his Mysterium Cosmographicum, Kepler proposed the structure of Solar system and the relationships between its extraterrestrial planets with the set of Platonic solids, inscribed and circumscribed by spherical orbs. Each solid encased in a sphere, within one another, would produce six layers, corresponding to the six known planets. Mercury, Venus, Earth, Mars, Jupiter, and Saturn. From innermost to outermost, these solids were arranged from octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and eventually the cube.^[55]

Constructions

The eleven nets of a cube

The cube has eleven different nets, which consist of an arrangement of edge-joined squares. These squares can be folded along the edges and connected to those polygons, which eventually become the faces of a cube.^[56][57]

In analytic geometry, a cube may be constructed using the Cartesian coordinate systems. For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are ${\displaystyle (\pm 1,\pm 1,\pm 1)}$.^[58] Its interior consists of all points ${\displaystyle (x_{0},x_{1},x_{2})}$ with ${\displaystyle -1<x_{i}<1}$ for all ${\displaystyle i}$. A cube's surface with center ${\displaystyle (x_{0},y_{0},z_{0})}$ and edge length of ${\displaystyle 2a}$ is the locus of all points ${\displaystyle (x,y,z)}$ such that $${\displaystyle \max\{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|\}=a.}$$

The cube is a Hanner polytope, because it can be constructed by using the Cartesian product of three line segments. Its dual polyhedron, the regular octahedron, is constructed by the direct sum of three line segments.^[59]

Representation

As a graph

Main article: Hypercube graph

The graph of a cube

The cube can be drawn into a graph, a structure in graph theory consisting of a set of vertices that are connected with an edge. It is attainable according to Steinitz's theorem, which states that a graph can be represented as the vertex-edge graph of a polyhedron, as long as it possesses the following two properties. These are planarity (the edges of a graph are connected to every vertex without crossing other edges), and 3-connected (whenever a graph with more than three vertices, and two of the vertices are removed, the edges remain connected).^[60][61] The skeleton of a cube, represented as the graph, is called the cubical graph, a Platonic graph. It has the same number of vertices and edges as the cube, twelve vertices and eight edges.^[62] The cubical graph is also classified as a prism graph, resembling the skeleton of a cuboid.^[63]

The cubical graph is a special case of hypercube graph or ${\displaystyle n}$-cube—denoted as ${\displaystyle Q_{n}}$—because it can be constructed by using the Cartesian product of graphs: two graphs connecting the pair of vertices with an edge to form a new graph.^[64] In the case of the cubical graph, it is the product of ${\displaystyle Q_{2}\mathbin {\Box } Q_{1}}$, where ${\displaystyle \mathbin {\Box } }$ denotes the Cartesian product of graphs. In other words, the cubical graph is constructed by connecting each vertex of two squares with an edge. Notationally, the cubical graph is ${\displaystyle Q_{3}}$.^[65] Like any hypercube graph, it has a cycle which visits every vertex exactly once,^[66] and it is also an example of a unit distance graph.^[67]

The cubical graph is bipartite, meaning every independent set of four vertices can be disjoint and the edges connected in those sets.^[68] However, every vertex in one set cannot connect all vertices in the second, so this bipartite graph is not complete.^[69] It is an example of both a crown graph and a bipartite Kneser graph.^[70][68]

In orthogonal projection

An object illuminated by parallel rays of light casts a shadow on a plane perpendicular to those rays, called an orthogonal projection. A polyhedron is considered equiprojective if, for some position of the light, its orthogonal projection is a regular polygon. The cube is equiprojective because, if the light is parallel to one of the four lines joining a vertex to the opposite vertex, its projection is a regular hexagon.^[71]

As a configuration matrix

Further information: Platonic solid § As a configuration

The cube can be represented as a configuration matrix, a matrix in which the rows and columns correspond to the elements of a polyhedron as the vertices, edges, and faces. The diagonal of a matrix denotes the number of each element that appears in a polyhedron, whereas the non-diagonal of a matrix denotes the number of the column's elements that occur in or at the row's element. The cube's eight vertices, twelve edges, and six faces are denoted by each element in a matrix's diagonal (8, 12, and 6). The first column of the middle row indicates that there are two vertices on each edge, denoted as 2; the middle column of the first row indicates that three edges meet at each vertex, denoted as 3. The configuration matrix of a cube is:^[72] $${\displaystyle {\begin{bmatrix}{\begin{matrix}8&3&3\\2&12&2\\4&4&6\end{matrix}}\end{bmatrix}}}$$

Related topics

Construction of polyhedra

Some of the polyhedra constructed based on a cube: the stellated octahedron, tetrakis hexahedron, and chamfered cube

Many polyhedra can be constructed based on a cube. Examples include:

• When faceting a cube, meaning removing part of the polygonal faces without creating new vertices of a cube, the resulting polyhedron is the stellated octahedron.^[73]
• New convex polyhedra can be constructed by attaching less-regular polyhedra to a cube's faces.^[10] The cube is thus a component of two Johnson solids, the elongated square pyramid and elongated square bipyramid, the latter being a cube with square pyramids on opposite faces.^[74]
• Attaching a low pyramid to each face of a cube produces its Kleetope, the tetrakis hexahedron,^[75] dual to the truncated octahedron.
• The barycentric subdivision of a cube (or its dual, the regular octahedron) is the disdyakis dodecahedron, a Catalan solid.^[76]
• The corner region of a cube can also be truncated by a plane (e.g., spanned by the three neighboring vertices), resulting in a trirectangular tetrahedron.^[77]
• The snub cube is an Archimedean solid that can be constructed by separating the cube's faces, and filling the gaps with twisted angle equilateral triangles, a process known as a snub.^[78]
• Each of the cube's vertices can be truncated, and the resulting polyhedron is the Archimedean solid, the truncated cube.^[79] When its edges are truncated, it is a rhombicuboctahedron.^[80] Relatedly, the rhombicuboctahedron can also be constructed by separating the cube's faces and then spreading away, after which adding other triangular and square faces between them; this is known as the "expanded cube". The same figure can be derived in the same way from the cube's dual, the regular octahedron.^[81]
• The chamfered cube is constructed from a cube by a truncating operator called chamfer. The resulting polyhedron has twelve hexagonal and six square centrally symmetric faces, a zonohedron.^[82][83]
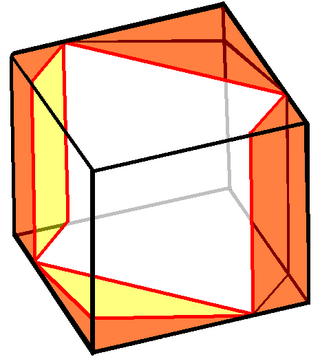
• Three mutually perpendicular golden rectangles can be constructed from a pair of vertices located on the midpoints of the opposite edges on a cube's surface, drawing a segment line between those two, and dividing that segment line in a golden ratio from its midpoint. The corners of these rectangles are the vertices of a regular icosahedron with twenty equilateral triangles.^[84]

The cube can be constructed with six square pyramids, tiling space by attaching their apices. In some cases, this produces the rhombic dodecahedron circumscribing a cube.^[85][86]

Polycubes

Main articles: Polycube and Dali cross

Two examples of polycubes are a polycube with five cubes attached face-to-face and Dalí cross. The latter is one of 261 nets of a tesseract.

A polycube is a solid figure formed by joining one or more equal cubes face-to-face. Polycubes are the three-dimensional analogues of two-dimensional polyominoes.^[87]

When four cubes are stacked vertically, and four others are attached to the second-from-top cube of the stack, the resulting polycube is the Dalí cross, named after Spanish surrealist artist Salvador Dalí, whose painting Corpus Hypercubus (1954) contains a tesseract unfolding into a six-armed cross; a similar construction is central to Robert A. Heinlein's short story "And He Built a Crooked House" (1940).^[88][89] The Dalí cross can be folded in a fourth dimension to enclose a tesseract.^[90] A cube is a three-dimensional instance of a hypercube (also known as a 3-cube); the two-dimensional hypercube (2-cube) is a square, and the four-dimensional hypercube (4-cube) is a tesseract.^[91]

Space-filling

Cubic honeycomb is an example of honeycomb in Euclidean three-dimensional space

A cube can achieve a honeycomb by filling together with its copy in three-dimensional space without leaving a gap. Cubes are space-fillings, where the phrase "space-filling" can be understood as a generalized tessellation.^[92] The cube is a plesiohedron, a special kind of space-filling polyhedron that can be defined as the Voronoi cell of a symmetric Delone set.^[93] The plesiohedra include the parallelohedra, which can be translated without rotating to fill a space in which each face of any of its copies is attached to a like face of another copy. There are five kinds of parallelohedra, one of which is the parallelepiped.^[94] Every three-dimensional parallelohedron is a zonohedron, a centrally symmetric polyhedron whose faces are centrally symmetric polygons.^[95]

An example of a honeycomb with a cubic type only, called a cell, is a cubic honeycomb that consists of four cubes around its edges in Euclidean three-dimensional space.^[96][97] More examples in three-dimensional non-Euclidean space are the honeycomb with three cubes around its edges in a three-dimensional sphere and the honeycomb with five cubes around its edges in hyperbolic space.^[97]

Any parallelepiped, including a cube, can achieve a honeycomb if its Dehn invariant is zero.^[98] The Dehn invariant's inception dates back to Hilbert's third problem, whether every two equal-volume polyhedra can always be dissected into polyhedral pieces and reassembled into each other. If yes, then the volume of any polyhedron could be defined axiomatically as the volume of an equivalent cube into which it could be reassembled. This problem was solved by Max Dehn, inventing his invariant, answering that not all polyhedra can be reassembled into a cube.^[99] It showed that two equal volume polyhedra should have the same Dehn invariant, except for the two tetrahedra whose Dehn invariants were different.^[100]

Miscellanea

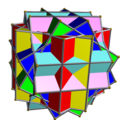
Enumeration according to Skilling (1976): compound of six cubes with rotational freedom ${\displaystyle \mathrm {UC} _{7}}$, three cubes ${\displaystyle \mathrm {UC} _{8}}$, and five cubes ${\displaystyle \mathrm {UC} _{9}}$

The polyhedral compounds, in which the cubes share the same centre, are uniform polyhedron compounds, meaning they are polyhedral compounds whose constituents are identical—although possibly enantiomorphous—uniform polyhedra, in an arrangement that is also uniform. Respectively, the list of compounds enumerated by Skilling (1976) in the seventh to ninth uniform compounds for the compound of six cubes with rotational freedom, three cubes, and five cubes.^[101] Two compounds, consisting of two and three cubes were found in Escher's wood engraving print Stars and Max Brückner's book Vielecke und Vielflache.^[102]

Spherical cube

A view in three-dimensional torus

The spherical cube represents the spherical polyhedron, which can be modeled with the arcs of great circles, creating bounds as the edges of a spherical square.^[103] Hence, the spherical cube consists of six spherical squares with 120° interior angles on each vertex. It has vector equilibrium, meaning that the distance from the centroid and each vertex is the same as the distance from that to each edge.^[104][105] Its dual is the spherical octahedron.^[103]

The topological object three-dimensional torus is a topological space defined to be homeomorphic to the Cartesian product of three circles. It can be represented as a three-dimensional model of the cube shape.^[106]

Fractal-shaped cubes are the Menger sponge, Jerusalem cube, and Mosely snowflake.

A cube can have fractal shapes, which retain the pattern shape recursively regardless of the magnification. The Menger sponge is an example of a fractal-shaped cube, analogous to the two-dimensional version, the Sierpiński carpet.^[107] Other varieties are the Jerusalem cube and Mosely snowflake.^[108][109]

See also

• Bhargava cube, a configuration to study the law of binary quadratic form and other such forms, of which the cube's vertices represent the integer.
• Chazelle polyhedron, a notched opposite faces of a cube.
• Cubism, an art movement of revolutionized painting and the visual arts.
• Hemicube, an abstract polyhedron produced by identifying opposite faces of a cube
• Kaaba, cubic buildings of importance to Islam.
• Magic cube, a magic square in three-dimensional version
• Schläfli double six, a configuration of 30 points and 12 lines in three-dimensional Euclidean space
• Squaring the square's three-dimensional analogue, cubing the cube
• Superellipsoid, a solid whose horizontal sections are of the same squareness
• Tychonoff cube, generalization of a unit cube