Top Qs
Timeline
Chat
Perspective
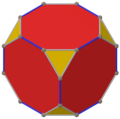
Truncated cube
Archimedean solid with 14 faces From Wikipedia, the free encyclopedia
Remove ads
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices.
| Truncated cube | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 14, E = 36, V = 24 (χ = 2) |
| Faces by sides | 8{3}+6{8} |
| Conway notation | tC |
| Schläfli symbols | t{4,3} |
| t0,1{4,3} | |
| Wythoff symbol | 2 3 | 4 |
| Coxeter diagram | |
| Symmetry group | Oh, B3, [4,3], (*432), order 48 |
| Rotation group | O, [4,3]+, (432), order 24 |
| Dihedral angle | 3-8: 125°15′51″ 8-8: 90° |
| References | U09, C21, W8 |
| Properties | Semiregular convex |
 Colored faces |
 3.8.8 (Vertex figure) |
 Triakis octahedron (dual polyhedron) |
 Net |

If the truncated cube has unit edge length, its dual triakis octahedron has edges of lengths 2 and δS +1, where δS is the silver ratio, √2 +1.
Remove ads
Area and volume
Summarize
Perspective
The area A and the volume V of a truncated cube of edge length a are:
Remove ads
Orthogonal projections
The truncated cube has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: triangles, and octagons. The last two correspond to the B2 and A2 Coxeter planes.
Remove ads
Spherical tiling
The truncated cube can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
Cartesian coordinates

Cartesian coordinates for the vertices of a truncated hexahedron centered at the origin with edge length 21/δS are all the permutations of
- (±1/δS, ±1, ±1),
where δS=√2+1.
If we let a parameter ξ= 1/δS, in the case of a Regular Truncated Cube, then the parameter ξ can be varied between ±1. A value of 1 produces a cube, 0 produces a cuboctahedron, and negative values produces self-intersecting octagrammic faces.
If the self-intersected portions of the octagrams are removed, leaving squares, and truncating the triangles into hexagons, truncated octahedra are produced, and the sequence ends with the central squares being reduced to a point, and creating an octahedron.
Remove ads
Dissection

The truncated cube can be dissected into a central cube, with six square cupolae around each of the cube's faces, and 8 regular tetrahedra in the corners. This dissection can also be seen within the runcic cubic honeycomb, with cube, tetrahedron, and rhombicuboctahedron cells.
This dissection can be used to create a Stewart toroid with all regular faces by removing two square cupolae and the central cube. This excavated cube has 16 triangles, 12 squares, and 4 octagons.[1][2]
Remove ads
Vertex arrangement
It shares the vertex arrangement with three nonconvex uniform polyhedra:
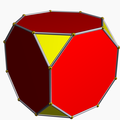 Truncated cube |
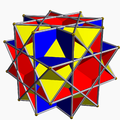 Nonconvex great rhombicuboctahedron |
 Great cubicuboctahedron |
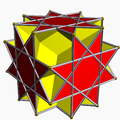 Great rhombihexahedron |
Related polyhedra
Summarize
Perspective
The truncated cube is related to other polyhedra and tilings in symmetry.
The truncated cube is one of a family of uniform polyhedra related to the cube and regular octahedron.
Symmetry mutations
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry, and a series of polyhedra and tilings n.8.8.
Alternated truncation
Tetrahedron, its edge truncation, and the truncated cube
Truncating alternating vertices of the cube gives the chamfered tetrahedron, i.e. the edge truncation of the tetrahedron.
The truncated triangular trapezohedron is another polyhedron which can be formed from cube edge truncation.
Remove ads
Related polytopes
The truncated cube, is second in a sequence of truncated hypercubes:
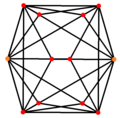
Truncated cubical graph
In the mathematical field of graph theory, a truncated cubical graph is the graph of vertices and edges of the truncated cube, one of the Archimedean solids. It has 24 vertices and 36 edges, and is a cubic Archimedean graph.[3] As a Hamiltonian cubic graph, it can be represented by LCF notation as LCF[2,-9,-2,2,9,-2]4.
See also
- Cube-connected cycles, a family of graphs that includes the skeleton of the truncated cube
- Chamfered cube, obtained by replacing the edges of a cube with non-uniform hexagons
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads