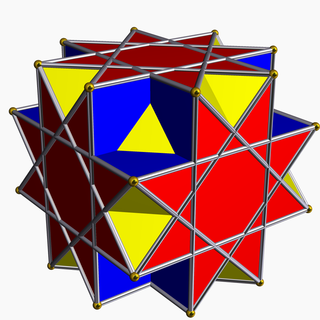
Great cubicuboctahedron
From Wikipedia, the free encyclopedia
In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14. It has 20 faces (8 triangles, 6 squares and 6 octagrams), 48 edges, and 24 vertices.[1] Its square faces and its octagrammic faces are parallel to those of a cube, while its triangular faces are parallel to those of an octahedron: hence the name cubicuboctahedron. The prefix great serves to distinguish it from the small cubicuboctahedron, which also has faces in the aforementioned directions.[2]
| Great cubicuboctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 20, E = 48 V = 24 (χ = −4) |
| Faces by sides | 8{3}+6{4}+6{8/3} |
| Coxeter diagram |     |
| Wythoff symbol | 3 4 | 4/3 4 3/2 | 4 |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U14, C50, W77 |
| Dual polyhedron | Great hexacronic icositetrahedron |
| Vertex figure |  3.8/3.4.8/3 |
| Bowers acronym | Gocco |
Orthographic projections
Related polyhedra
It shares the vertex arrangement with the convex truncated cube and two other nonconvex uniform polyhedra. It additionally shares its edge arrangement with the nonconvex great rhombicuboctahedron (having the triangular faces and 6 square faces in common), and with the great rhombihexahedron (having the octagrammic faces in common).
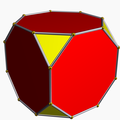 Truncated cube |
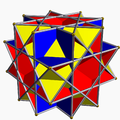 Nonconvex great rhombicuboctahedron |
Great cubicuboctahedron |
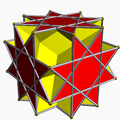 Great rhombihexahedron |
Great hexacronic icositetrahedron
| Great hexacronic icositetrahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 24, E = 48 V = 20 (χ = −4) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU14 |
| dual polyhedron | Great cubicuboctahedron |
The great hexacronic icositetrahedron (or great lanceal disdodecahedron) is the dual of the great cubicuboctahedron.
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.