Top Qs
Timeline
Chat
Perspective
Rectified 7-cubes
From Wikipedia, the free encyclopedia
Remove ads
In seven-dimensional geometry, a rectified 7-cube is a convex uniform 7-polytope, being a rectification of the regular 7-cube.
There are unique 7 degrees of rectifications, the zeroth being the 7-cube, and the 6th and last being the 7-cube. Vertices of the rectified 7-cube are located at the edge-centers of the 7-ocube. Vertices of the birectified 7-cube are located in the square face centers of the 7-cube. Vertices of the trirectified 7-cube are located in the cube cell centers of the 7-cube.
Remove ads
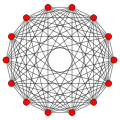
Rectified 7-cube
| Rectified 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | r{4,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | 128 + 14 |
| 5-faces | 896 + 84 |
| 4-faces | 2688 + 280 |
| Cells | 4480 + 560 |
| Faces | 4480 + 672 |
| Edges | 2688 |
| Vertices | 448 |
| Vertex figure | 5-simplex prism |
| Coxeter groups | B7, [3,3,3,3,3,4] |
| Properties | convex |
Alternate names
- rectified hepteract (Acronym rasa) (Jonathan Bowers)[1]
Images
Cartesian coordinates
Cartesian coordinates for the vertices of a rectified 7-cube, centered at the origin, edge length are all permutations of:
- (±1,±1,±1,±1,±1,±1,0)
Remove ads
Birectified 7-cube
Alternate names
- Birectified hepteract (Acronym bersa) (Jonathan Bowers)[2]
Images
Cartesian coordinates
Cartesian coordinates for the vertices of a birectified 7-cube, centered at the origin, edge length are all permutations of:
- (±1,±1,±1,±1,±1,0,0)
Remove ads
Trirectified 7-cube
Alternate names
- Trirectified hepteract
- Trirectified 7-orthoplex
- Trirectified heptacross (Acronym sez) (Jonathan Bowers)[3]
Images
Cartesian coordinates
Cartesian coordinates for the vertices of a trirectified 7-cube, centered at the origin, edge length are all permutations of:
- (±1,±1,±1,±1,0,0,0)
Related polytopes
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads