Top Qs
Timeline
Chat
Perspective
Truncated infinite-order triangular tiling
From Wikipedia, the free encyclopedia
Remove ads
In geometry, the truncated infinite-order triangular tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of t{3,∞}.
Remove ads
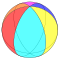
Symmetry




 .
.The dual of this tiling represents the fundamental domains of *∞33 symmetry. There are no mirror removal subgroups of [(∞,3,3)], but this symmetry group can be doubled to ∞32 symmetry by adding a mirror.
Remove ads
Related polyhedra and tiling
Summarize
Perspective
This hyperbolic tiling is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (6.n.n), and [n,3] Coxeter group symmetry.
Remove ads
See also
Wikimedia Commons has media related to Uniform tiling 6-6-i.
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads