Rhombitriapeirogonal tiling

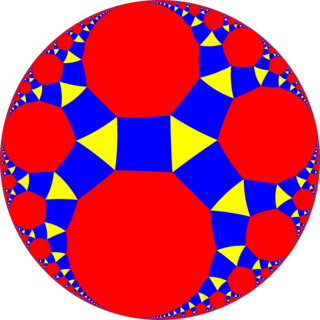
In geometry, the rhombtriapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of rr{∞,3}.

Rhombitriapeirogonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	3.4.∞.4
Schläfli symbol	rr{∞,3} or ${\displaystyle r{\begin{Bmatrix}\infty \\3\end{Bmatrix}}}$ s2{3,∞}
Wythoff symbol	3 | ∞ 2
Coxeter diagram	or
Symmetry group	[∞,3], (*∞32) [∞,3+], (3*∞)
Dual	Deltoidal triapeirogonal tiling
Properties	Vertex-transitive

Symmetry

This tiling has [∞,3], (*∞32) symmetry. There is only one uniform coloring.

Similar to the Euclidean rhombitrihexagonal tiling, by edge-coloring there is a half symmetry form (3*∞) orbifold notation. The apeireogons can be considered as truncated, t{∞} with two types of edges. It has Coxeter diagram , Schläfli symbol s₂{3,∞}. The squares can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, an infinite-order triangular tiling results, constructed as a snub triapeirotrigonal tiling, .

Related polyhedra and tiling

Paracompact uniform tilings in [∞,3] family v t e
Symmetry: [∞,3], (*∞32)							[∞,3]+ (∞32)	[1+,∞,3] (*∞33)		[∞,3+] (3*∞)
		=	=	=				= or	= or	=
{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h2{∞,3}	s{3,∞}
Uniform duals
V∞3	V3.∞.∞	V(3.∞)2	V6.6.∞	V3∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)3		V3.3.3.3.3.∞

Symmetry mutations

This hyperbolic tiling is topologically related as a part of sequence of uniform cantellated polyhedra with vertex configurations (3.4.n.4), and [n,3] Coxeter group symmetry.

*n32 symmetry mutation of expanded tilings: 3.4.n.4 v t e
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figure
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4	3.4.12i.4	3.4.9i.4	3.4.6i.4

See also

• List of uniform planar tilings
• Tilings of regular polygons
• Uniform tilings in hyperbolic plane