Truncated triapeirogonal tiling

In geometry, the truncated triapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of tr{∞,3}.

Truncated triapeirogonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.6.∞
Schläfli symbol	tr{∞,3} or ${\displaystyle t{\begin{Bmatrix}\infty \\3\end{Bmatrix}}}$
Wythoff symbol	2 ∞ 3 |
Coxeter diagram	or
Symmetry group	[∞,3], (*∞32)
Dual	Order 3-infinite kisrhombille
Properties	Vertex-transitive

Symmetry

Truncated triapeirogonal tiling with mirrors

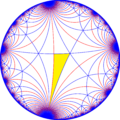
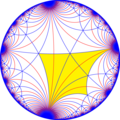
The dual of this tiling represents the fundamental domains of [∞,3], *∞32 symmetry. There are 3 small index subgroup constructed from [∞,3] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

A special index 4 reflective subgroup, is [(∞,∞,3)], (*∞∞3), and its direct subgroup [(∞,∞,3)]⁺, (∞∞3), and semidirect subgroup [(∞,∞,3⁺)], (3*∞).^[1] Given [∞,3] with generating mirrors {0,1,2}, then its index 4 subgroup has generators {0,121,212}.

An index 6 subgroup constructed as [∞,3*], becomes [(∞,∞,∞)], (*∞∞∞).

Small index subgroups of [∞,3], (*∞32)

Index	1	2		3	4	6		8	12	24
Diagrams
Coxeter (orbifold)	[∞,3] = (*∞32)	[1+,∞,3] = (*∞33)	[∞,3+] (3*∞)	[∞,∞] (*∞∞2)	[(∞,∞,3)] (*∞∞3)	[∞,3*] = (*∞3)	[∞,1+,∞] (*(∞2)2)	[(∞,1+,∞,3)] (*(∞3)2)	[1+,∞,∞,1+] (*∞4)	[(∞,∞,3*)] (*∞6)
Direct subgroups
Index	2	4		6	8	12		16	24	48
Diagrams
Coxeter (orbifold)	[∞,3]+ = (∞32)	[∞,3+]+ = (∞33)		[∞,∞]+ (∞∞2)	[(∞,∞,3)]+ (∞∞3)	[∞,3*]+ = (∞3)	[∞,1+,∞]+ (∞2)2	[(∞,1+,∞,3)]+ (∞3)2	[1+,∞,∞,1+]+ (∞4)	[(∞,∞,3*)]+ (∞6)

Related polyhedra and tiling

Paracompact uniform tilings in [∞,3] family v t e
Symmetry: [∞,3], (*∞32)							[∞,3]+ (∞32)	[1+,∞,3] (*∞33)		[∞,3+] (3*∞)
		=	=	=				= or	= or	=
{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h2{∞,3}	s{3,∞}
Uniform duals
V∞3	V3.∞.∞	V(3.∞)2	V6.6.∞	V3∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)3		V3.3.3.3.3.∞

This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

*n32 symmetry mutation of omnitruncated tilings: 4.6.2n v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

See also

• List of uniform planar tilings
• Tilings of regular polygons
• Uniform tilings in hyperbolic plane

References

1. Norman W. Johnson and Asia Ivic Weiss, Quadratic Integers and Coxeter Groups, Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.