三次曲線

数学において、三次曲線（さんじきょくせん、英: cubic）、特にユークリッド幾何学における平面三次曲線（英: cubic plane curve）は以下のような三次方程式によって定義される代数曲線である。

${\displaystyle F(x,y,z)=0}$

三次曲線の種類

ここで${\displaystyle (x:y:z)}$は射影平面上の斉次座標、またはアフィン空間の非斉次座標でz = 1とした座標で、Fは三次の斉次多項式、すなわち以下のような0でない三次単項式の線形結合とする。

${\displaystyle x^{3},y^{3},z^{3},x^{2}y,x^{2}z,y^{2}x,y^{2}z,z^{2}x,z^{2}y,xyz}$

これら10個の項から成ることより、三次曲線は任意の可換体K上で9次元の射影空間を成す。また三次曲線Cを満たす1点Pは1つの線形条件を課す。したがって9つの点を通る三次曲線はただ一つに決定される。 5つの点で決定する円錐曲線と比較してみると、2つの三次曲線が9つの点を通るならば、それらは束を成し、さらなる性質を持つこととなる（ケイリー＝バッハラッハの定理）。

特異的な三次曲線 y² = x² ⋅ (x + 1). 媒介変数表示 t ↦ (t² – 1, t ⋅ (t² – 1)).

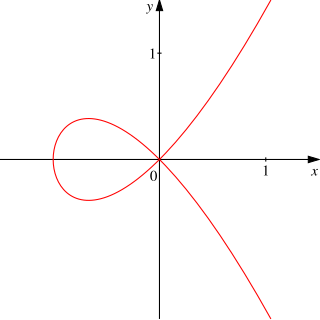
三次曲線には特異点を持つものもあり、射影直線におけるパラメトリック方程式となる。一方、 特異点を持たない三次曲線は複素数のような代数的閉体上に9つの変曲点を持つ^[1]。これは、三次曲線を再定義するヘッセ行列の同次座標をCと掛け合わせることにより示すことができる（ベズーの定理）。しかし、これらの点のうちは実射影平面上にあるのは3点だけであり^[2]、他の点は実射影平面上で曲線を描いても見ることはできない。特異点を持たない三次曲線の9つの変曲点は、そのうちの2つを通るすべての直線がちょうど3つの変曲点を含むという性質を持っている。

実射影平面上にある変曲点はニュートンによって研究され、非特異な三次曲線の実点が1つか2つの「オーバル」を通ることが発見された。 これらのオーバルのうちの1つは、すべて射影直線を横切るので、ユークリッド平面に描いたときには見ることができず、3つの実変曲点を含む、1本または3本の無限の分岐として現れる。もう1つのオーバルは、存在するとしても変曲点を含まず、オーバルか2つの無限の分岐のように見える。 円錐曲線の断面の様に直線はオーバルを最大2点で切断する。

非特異な三次曲線はK上の楕円曲線でもある。楕円曲線は普通、ワイエルシュトラスの楕円関数を変形したもので研究されており、三次関数の平方根で作られた有理関数上で定義されている。これはワイエルシュトラス標準形の無限遠点としてはたらくK-有理点に依存する。Kが有理数体のとき多くの三次曲線はそのような点を持たない。

尖点や二重点など、特異的な三次曲線の特異点は限られている。 そのような3次曲線は、2次曲線と直線、または3つの直線に退化する。したがって2次曲線と直線の場合は、2つのニ重点または二重尖点（英語版）、3つの直線の場合はまたは3つのニ重点か1つの三重点（共点）を持つ。

三角形の三次曲線

△ABCの辺について ${\displaystyle a=|BC|,}$ ${\displaystyle b=|CA|,}$ ${\displaystyle c=|AB|}$ とする。△ABCの有名な三次曲線は様々な三角形の中心を通る。以下は斉次座標である三線座標と重心座標を用いる。

三線座標から重心座標への変換は以下の様に行われれる。

${\displaystyle x\to bcx,\quad y\to cay,\quad z\to abz;}$

重心座標から三線座標への変換は以下の様に行われれる。

${\displaystyle x\to ax,\quad y\to by,\quad z\to cz.}$

三次曲線の多くは以下の形式で表される。

${\displaystyle f(a,b,c,x,y,z)+f(b,c,a,y,z,x)+f(c,a,b,z,x,y)=0.}$

この式は下記のような上の式を略した表記を用いることもある。

${\displaystyle \sum _{\text{cyclic}}f(x,y,z,a,b,c)=0}$.

またXの等角共役点をX*とする。このとき三線座標において ${\displaystyle X=x:y:z}$ ならば ${\displaystyle X^{*}={\tfrac {1}{x}}:{\tfrac {1}{y}}:{\tfrac {1}{z}}}$が成り立つ。

ノイベルグ三次曲線

→詳細は「ノイベルグ三次曲線」を参照

△ABCのノイベルグ三次曲線 Xを辺BC, CA, ABで鏡映した点をX_A, X_B, X_CとしAX_A, BX_B, CX_Cが一点で交わるようなXの軌跡である。

三線座標: ${\displaystyle \sum _{\text{cyclic}}(\cos {A}-2\cos {B}\cos {C})x(y^{2}-z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}(a^{2}(b^{2}+c^{2})+(b^{2}-c^{2})^{2}-2a^{4})x(c^{2}y^{2}-b^{2}z^{2})=0}$

ノイベルグ三次曲線（Neuberg cubic）はX*が直線EX上（Eはオイラー無限遠点X(30)、オイラー線方向の無限遠点）にあるような点Xの軌跡、つまりXX*がオイラー線と平行になるような点の軌跡である。Xを辺BC, CA, ABで鏡映した点をX_A, X_B, X_Cとし、△X_AX_BX_Cと△ABCが配景なXの軌跡とも定義される。

ノイベルグ三次曲線は頂点、内心と傍心、外心、垂心、フェルマー点、等力点、オイラー無限遠点などを通る。

Cubics in the Triangle PlaneではK001と登録されている。

17点三次曲線（Thomson Cubic）

→詳細は「17点3次曲線」を参照

17点三次曲線（黒い線）。17点三次曲線上のX ,X*,X(2)(重心)は共線である。

三線座標: ${\displaystyle \sum _{\text{cyclic}}bcx(y^{2}-z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}x(c^{2}y^{2}-b^{2}z^{2})=0}$

17点三次曲線はX*が直線GX（Gは重心）上にあるような点Xの軌跡である。

17点三次曲線は頂点、内心と傍心、重心、外心、垂心、類似重心、辺の中点などを通る。

Cubics in the Triangle PlaneではK002 として登録されている。

ダルブー三次曲線

→詳細は「ダルブー三次曲線（オランダ語版）」を参照

ダルブー三次曲線、 XのBC, CA, ABに対する垂足三角形が元の三角形と配景的であるようなXの軌跡

三線座標:${\displaystyle \sum _{\text{cyclic}}(\cos {A}-\cos {B}\cos {C})x(y^{2}-z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}(2a^{2}(b^{2}+c^{2})+(b^{2}-c^{2})^{2}-3a^{4})x(c^{2}y^{2}-b^{2}z^{2})=0}$

ダルブー三次曲線（Darboux Cubic）はX*が直線LX上（Lはド・ロンシャン点）にあるような点Xの軌跡である。ダルブー三次曲線上のXの垂足三角形はチェバ三角形で、チェバ三角形の元の点はリュカ三次曲線を成す。また、X の垂足三角形はXの反チェバ三角形と配景的で、その配景の中心はトムソン三次曲線を成す。

ダルブー三次曲線は頂点、内心と傍心、外心、垂心、ドロンシャン点、頂点の外接円に対する対蹠点などを通る。

Cubics in the Triangle Planeでは、K004 として登録されている。

ナポレオン-フォイエルバッハ三次曲線

三線座標: ${\displaystyle \sum _{\text{cyclic}}\cos(B-C)x(y^{2}-z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}(a^{2}(b^{2}+c^{2})+(b^{2}-c^{2})^{2})x(c^{2}y^{2}-b^{2}z^{2})=0}$

ナポレオン-フォイエルバッハ三次曲線（Napoleon-Feuerbach cubic）はX*が直線NX上（N = X(5),九点円の中心）にある点Xの軌跡である。

ナポレオン-フォイエルバッハ三次曲線は頂点、内心と傍心、外心、垂心、ナポレオン点などを通る。

Cubics in the Triangle Planeでは K005 として登録されている。

リュカ三次曲線

→詳細は「リュカ三次曲線」を参照

リュカ三次曲線 、 Xののチェバ三角形 がダルブー三次曲線上の点の垂足三角形となるような点Xの軌跡。

三線座標: ${\displaystyle \sum _{\text{cyclic}}\cos(A)x(b^{2}y^{2}-c^{2}z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}(b^{2}+c^{2}-a^{2})x(y^{2}-z^{2})=0}$

リュカ三次曲線（Lucas cubic）はX のチェバ三角形がダルブ―三次曲線上の点の垂足三角形となるような点Xの軌跡である。

リュカ三次曲線は頂点、反中点三角形の頂点、シュタイナー外接楕円の焦点、重心、垂心、ジェルゴンヌ点、ナーゲル点、ド・ロンシャン点 などを通る。

Cubics in the Triangle PlaneではK007 として登録されている。

第一ブロカール三次曲線

第一ブロカール三次曲線、第一ブロカール三角形を△A'B'C' とし、XA', XB', XC'とBC, CA, CB,のそれぞれの交点が共線であるような点Xの軌跡。

三線座標:${\displaystyle \sum _{\text{cyclic}}bc(a^{4}-b^{2}c^{2})x(y^{2}+z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}(a^{4}-b^{2}c^{2})x(c^{2}y^{2}+b^{2}z^{2})=0}$

△A'B'C' を第一ブロカール三角形（1st Brocard cubic）、X_A, X_B, X_C.をそれぞれXA′, XB′, XC′と BC, CA, AB,の交点とする。このときX_A, X_B, X_Cが共線となるような点Xの軌跡を第一ブロカール三次曲線と言う。

第一ブロカール三次曲線は頂点、第一,第三ブロカール点の頂点、重心、類似重心、シュタイナー点などを通る。

Cubics in the Triangle Planeでは K017として登録されている。

第二ブロカール三次曲線

三線座標: ${\displaystyle \sum _{\text{cyclic}}bc(b^{2}-c^{2})x(y^{2}+z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}(b^{2}-c^{2})x(c^{2}y^{2}+b^{2}z^{2})=0}$

第二ブロカール三次曲線（2nd Brocard cubic）は直線XX*の、X,X*を通る外接円錐曲線に対する極がブロカール軸上にあるような点Xの軌跡である。頂点、重心、類似重心、フェルマー点、等力点、パリー点、第二,第四ブロカール三角形の頂点を通る。

Cubics in the Triangle Planeでは K018として登録されている。

1st equal areas cubic

第一等積三次曲線:X のチェバ三角形とX*のチェバ三角形の面積が等しくなるような点Xの軌跡。

三線座標: ${\displaystyle \sum _{\text{cyclic}}a(b^{2}-c^{2})x(y^{2}-z^{2})=0}$

重心座標: ${\displaystyle \sum _{\text{cyclic}}a^{2}(b^{2}-c^{2})x(c^{2}y^{2}-b^{2}z^{2})=0}$

1st equal areas cubicはX のチェバ三角形とX*のチェバ三角形の面積が等しくなるような点Xの軌跡である。X*が直線S*X 上(S = X(99),シュタイナー点)にあるような点Xの軌跡とも定義される。

1st equal areas cubicは内心と傍心、シュタイナー点 、第一,第二ブロカール点を通る。

Cubics in the Triangle Planeでは K021として登録されている。

2nd equal areas cubic

三線座標: ${\displaystyle (bz+cx)(cx+ay)(ay+bz)=(bx+cy)(cy+az)(az+bx)}$

重心座標:${\displaystyle \sum _{\text{cyclic}}a(a^{2}-bc)x(c^{3}y^{2}-b^{3}z^{2})=0}$

2nd equal areas cubicは三線座標で ${\displaystyle X=x:y:z}$ , ${\displaystyle X_{Y}=y:z:x}$, ${\displaystyle X_{Z}=z:x:y.}$ とし、X_YとX_Zのチェバ三角形の面積が等しくなるような点Xの軌跡である。

2nd equal areas cubicは内心、重心、類似重心 X(31), X(105), X(238), X(292), X(365), X(672), X(1453), X(1931), X(2053)などを通る。

Cubics in the Triangle Planeでは K155として登録されている。