상위 질문
타임라인
채팅
관점
내적 공간
위키백과, 무료 백과사전
Remove ads
선형대수학과 함수해석학에서 내적 공간(內積空間, 영어: inner product space)은 두 벡터의 쌍에 스칼라를 대응시키는 일종의 함수가 주어진 벡터 공간이다. 내적 공간 위에서는 벡터의 길이나 각도 등의 개념을 다룰 수 있다. 스칼라곱을 갖춘 유클리드 공간의 일반화이다.
정의
요약
관점
-벡터 공간 위의 내적(內積, 영어: inner product)은 양의 정부호 에르미트 반쌍선형 형식이다. (실수의 경우 이는 양의 정부호 대칭 쌍선형 형식과 같다.) 즉, 다음 조건들을 만족시키는 함수
이다.
이들 성질로부터 내적의 다음과 같은 성질을 유도할 수 있다.
- (오른쪽 반쌍선형성) 임의의 및 에 대하여,
내적이 주어진 -벡터 공간 을 -내적 공간이라고 한다. 특히 인 경우, 즉 복소수체 위의 내적 공간은 유니터리 공간(영어: unitary space)이라고 부르기도 한다.
Remove ads
성질
요약
관점
노름 구조
-내적 공간 위에 자연스러운 -노름 공간 구조를 다음과 같이 줄 수 있다.
증명:
노름의 양의 정부호성과 양의 동차성은 내적의 정의에 따라 자명하다. 노름의 삼각 부등식은 코시-슈바르츠 부등식의 따름정리이며, 그 증명은 다음과 같다. 임의의 벡터 에 대하여,
이므로,
반대로, -노름 공간이 -내적 공간으로부터 유도될 필요충분조건은 평행 사변형 법칙
이다. 이 경우, 가능한 유일한 내적은 다음과 같으며, 이를 극화 항등식(極化恒等式, 영어: polarization identity)이라고 한다.
증명:
실수 내적 공간의 경우만을 증명하자. 극화 항등식이 정의한 내적이 다음 네 가지를 보이는 것으로 족하다.
첫째와 둘째 조건은 자명하다. 셋째 조건은 다음과 같이 증명된다.
넷째 조건의 의 경우는 다음과 같이 증명된다.
또한, 일 경우의 증명은 다음과 같다.
만약 일 경우, ()이라고 하자. 그렇다면, 다음과 같이 증명된다.
마지막으로, 일 경우는 를 고정하였을 때 가 연속 함수임에 따라 성립한다.
코시-슈바르츠 부등식
내적 공간 의 벡터 에 대하여, 다음과 같은 부등식이 성립하며, 이를 코시-슈바르츠 부등식이라고 한다.
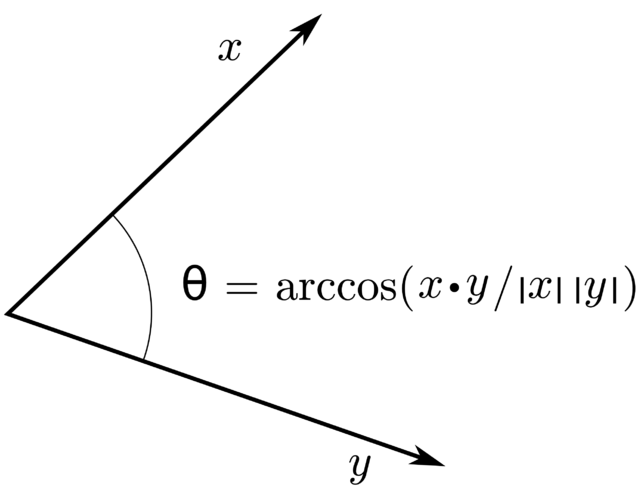
이에 따라, 두 벡터 사이의 각도를 다음과 같이 정의할 수 있다.
또한, 내적이 유도하는 노름의 삼각 부등식은 코시-슈바르츠 부등식을 통해 증명된다.
정규 직교 기저
내적 공간 의 정규 직교 기저(正規直交基底, 영어: orthonormal basis)는 서로 다른 두 벡터의 내적이 항상 0인 단위 벡터들이 이루는 기저이다. 즉, 이는 다음 조건들을 만족시키는 기저 이다.
- (직교성) 만약 이며 라면,
- (정규성) 임의의 에 대하여,
유한 차원 내적 공간의 정규 직교 기저는 항상 존재한다. 이는 그람-슈미트 과정을 통해 구성할 수 있다.
내적 공간 의 벡터 의 정규 직교 기저 에 대한 좌표는 다음과 같다.
또한, 이 좌표 아래 내적을 다음과 같이 나타낼 수 있다.
내적 공간 속의 유한 정규 직교 집합 및 벡터 에 대하여, 베셀 부등식과 유사한 꼴의 다음과 같은 부등식이 성립한다.
선형 범함수
유한 차원 내적 공간 의 모든 선형 범함수는 어떤 유일한 고정된 벡터 와의 내적
이다. 구체적으로, 정규 직교 기저 가 주어졌을 때, 선형 범함수 를 나타내는 벡터는 다음과 같다.
이에 따라, 유한 차원 내적 공간의 선형 변환 의 수반 선형 변환 은 다음과 같이 항상 존재한다.
그러나 무한 차원 내적 공간의 경우 일반적으로 성립하지 않는다. 예를 들어, 다항식환 에 다음과 같은 내적을 정의할 수 있다.
이 경우, 임의의 가 주어졌을 때, 다음과 같은 선형 범함수는 고정된 벡터와의 내적으로 나타낼 수 없다.
또한 미분 선형 변환
의 수반 선형 변환은 존재하지 않는다.
Remove ads
예
요약
관점
유한 차원 벡터 공간 위의 내적
차원 -벡터 공간 위의 표준적인 내적은 다음과 같다.
일 때, 은 유클리드 공간이며, 이 내적은 스칼라곱이라고 부른다. 이 경우 실수의 켤레 복소수는 스스로와 일치한다 (). 이 내적이 유도하는 노름은 L2 노름이다. 그러나 의 경우, Lp 노름은 평행 사변형 법칙을 만족시키지 않으므로 내적으로부터 유도될 수 없다.
특히, 인 경우 는 1차원 벡터 공간이며, 위 내적은 단순히
이다.
마찬가지로, 실수 또는 복소수 성분 행렬들의 집합 은 차원 벡터 공간을 이룬다. 이 위에 다음과 같은 내적을 정의할 수 있다.
이를 프로베니우스 내적이라고 한다.
보다 일반적으로, 양의 정부호 행렬 에 대하여, 위에 다음과 같은 내적을 정의할 수 있다.
함수 공간
연속 함수의 공간 에는 다음과 같은 내적을 정의할 수 있다.
여기서 우변의 적분은 리만 적분이다. 또한, 다음과 같은 내적을 정의할 수도 있다.
가측 함수 들의 (거의 어디서나 같음에 대한) 동치류들로 구성된 -벡터 공간 위에 다음과 같은 내적을 정의할 수 있다.
여기서 우변은 르베그 적분이다. 이를 L2 공간이라고 한다. 특히, 가 확률 공간일 때, 은 확률 변수들의 동치류들로 이루어지며, 적분은 기댓값이다. 따라서, 두 확률 변수 의 내적은 다음과 같다.
가측 함수나 확률 변수의 동치류를 취하는 것은 내적을 양의 정부호적이게 만들기 위함이다. 예를 들어, 일 필요충분조건은 거의 확실하게 인 것이다 (). 따라서, 스스로와의 내적이 0인 경우가 0밖에 없으려면 거의 어디서나 같은 함수들을 하나의 동치류로 뭉뚱그려야 한다.
Remove ads
같이 보기
참고 문헌
- Hoffman, Kenneth; Kunze, Ray (1971). 《Linear algebra》 (영어) 2판. Englewood Cliffs, N. J.: Prentice-Hall. ISBN 0-13-536797-2. MR 0276251. Zbl 0212.36601. Internet Archive LinearAlge(…).
외부 링크
- “Inner product”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Inner product space”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Inner product”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Inner product space”. 《PlanetMath》 (영어).
- “Inner product”. 《PlanetMath》 (영어).
- “Inner product space”. 《nLab》 (영어).
- “Norms Induced by Inner Products and the Parallelogram Law”. 《Stack Exchange》 (영어). 2018년 2월 3일에 원본 문서에서 보존된 문서. 2018년 2월 2일에 확인함.
Remove ads
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



























































![{\displaystyle \mathbb {C} [x]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/244ad3bb0a1d2ff11dde84c4edee1171f670fdb0)


![{\displaystyle \mathbb {C} [x]\to \mathbb {C} }](http://wikimedia.org/api/rest_v1/media/math/render/svg/9d558256d59a9e57600b29dfa41b1ea40536e2d0)

![{\displaystyle D\colon \mathbb {C} [x]\to \mathbb {C} [x]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/147f3517575449593fb89c5f10982da0482360a7)















![{\displaystyle {\mathcal {C}}([a,b];\mathbb {K} )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bf8933ab5ab86c9815b8724c9fd639c38f060b31)










