랭뮤어 흡착 모델

랭뮤어 흡착 모델(영어: Langmuir adsorption model)은 흡착을 설명하기 위해 흡착질이 등온과정에서 이상 기체처럼 행동한다고 가정한다. 이 모형에 따르면, 흡착과 탈착은 가역적인 과정이다. 이 모형은 압력의 효과도 설명한다. 즉, 이러한 조건에서 흡착질의 부분 압력 ${\displaystyle p_{A}}$는 고체 흡착제에 흡착된 부피 V와 관련된다. 그림에 나타난 바와 같이 흡착제는 흡착질을 결합할 수 있는 일련의 구별되는 자리로 구성된 이상적인 고체 표면이라고 가정한다. 흡착질 결합은 흡착질 기체 분자 ${\displaystyle A_{\text{g}}}$와 빈 흡착 자리 S 사이의 화학 반응으로 취급된다. 이 반응은 평형 상수 ${\displaystyle K_{\text{eq}}}$와 관련된 흡착된 종 ${\displaystyle A_{\text{ad}}}$를 생성한다.

${\displaystyle {\ce {A_{g}{}+ S <=> A_{ad}}}}$.

모델에 사용된 기본 가정을 명확히 보여주는 동일한 흡착 자리, 점유된(파란색) 및 비어있는(빨간색) 자리를 나타내는 도식. 흡착 자리(굵은 점)는 동일하며 단위 점유율을 가질 수 있다. 또한, 흡착물은 표면에서 이동하지 않는다.

이러한 기본 가설로부터 랭뮤어 흡착 등온식의 수학적 공식은 화학 반응속도론적, 열역학적, 그리고 통계역학적 접근 방식으로 각각 독립적이고 상보적인 방식으로 유도될 수 있다(다양한 증명은 아래 참조).

랭뮤어 흡착 방정식은 다음과 같다.

${\displaystyle \theta _{A}={\frac {V}{V_{\text{m}}}}={\frac {K_{\text{eq}}^{A}\,p_{A}}{1+K_{\text{eq}}^{A}\,p_{A}}},}$

여기서 ${\displaystyle \theta _{A}}$는 흡착 자리의 분율 점유율이다. 즉, 고체에 흡착된 기체의 부피 V와 고체 표면 전체를 덮고 흡착물로 완전히 점유된 기체 분자 단일층의 부피 ${\displaystyle V_{\text{m}}}$의 비율이다. 균일하고 평평한 고체 표면을 덮는 흡착물 분자의 연속적인 단일층은 이 흡착 모형의 개념적 기초이다.^[1]

배경 및 실험

1916년, 어빙 랭뮤어는 단순 표면에 종이 흡착되는 모델을 제시했다. 랭뮤어는 표면 화학에 대한 연구로 1932년 노벨 화학상을 수상했다. 랭뮤어는 주어진 표면에 종이 물리흡착 또는 화학흡착으로 "달라붙을" 수 있는 일정한 수의 동일한 자리가 있다고 가정했다. 그의 이론은 기체 분자가 표면에서 탄력적으로 튀어 오르지 않고 고체 내부의 분자 그룹과 유사한 방식으로 표면에 붙잡힌다는 가정에서 시작되었다.^[2]

랭뮤어는 흡착된 막이 한 분자 두께를 초과하지 않는다는 가정을 확인하는 두 편의 논문을 발표했다. 첫 번째 실험은 기체 속에서 가열된 필라멘트에서 방출되는 전자를 관찰하는 것이었다.^[3] 두 번째 실험은 더 직접적인 증거로, 흡착제 표면층에 있는 액체 막을 조사하고 측정했다. 랭뮤어는 또한 일반적으로 표면과 흡착된 물질의 첫 번째 층 사이의 인력이 첫 번째 층과 두 번째 층 사이의 인력보다 훨씬 크다는 점을 지적했다. 그러나 올바른 온도와 압력 조합이 주어지면 후속 층이 응축될 수 있는 경우도 있다.^[4]

모델의 기본 가정

이 모델에 내재된 다음 가정^[5]은 가장 간단한 경우, 즉 단일 흡착물이 고체 표면의 일련의 동일한 자리에 흡착되는 경우에 특히 유효하다.

1. 흡착 자리를 포함하는 표면은 주름이 없는 완벽하게 평평한 평면이다(표면이 균일하다고 가정). 그러나 화학적으로 불균일한 표면도 흡착물이 표면의 한 가지 기능기 유형에만 결합하는 경우 균일하다고 간주될 수 있다.
2. 흡착하는 기체는 비이동 상태로 흡착된다.
3. 모든 자리는 에너지적으로 동일하며, 흡착 에너지는 모든 자리에서 동일하다.
4. 각 자리는 최대 하나의 분자만 수용할 수 있다(단일층만 덮는다).
5. 인접한 자리의 흡착물 분자 간에는 상호작용이 없거나(이상적인) 상호작용이 있다. 상호작용이 이상적일 경우, 측면 상호작용 에너지는 표면 점유율과 관계없이 모든 자리에서 동일하다.

랭뮤어 흡착 등온식의 유도

하나의 흡착종만을 포함하는 랭뮤어 흡착 등온식의 수학적 표현은 화학 반응속도론적 접근법, 열역학적 접근법, 그리고 통계역학적 접근법 등 다양한 방법으로 증명될 수 있다. 두 개의 경쟁적인 흡착종이 있는 경우에는 경쟁적 흡착 모델이 필요하며, 흡착된 종이 두 개의 별개의 독립체로 해리되는 경우에는 해리성 흡착 모델을 사용해야 한다.

동역학적 유도

이 섹션^[5]에서는 단일 흡착물 경우에 대한 화학 반응속도론적 유도를 제공한다. 동역학적 유도는 기체상 흡착에 적용된다. 다중 흡착물 경우는 경쟁적 흡착 하위 섹션에서 다룬다. 이 모델은 흡착과 탈착을 기본 과정으로 가정하며, 흡착 속도 r_ad와 탈착 속도 r_d는 다음과 같이 주어진다.

${\displaystyle r_{\text{ad}}=k_{\text{ad}}p_{A}[S],}$

${\displaystyle r_{\text{d}}=k_{d}[A_{\text{ad}}],}$

여기서 p_A는 표면 위 A의 부분 압력, [S]는 자유 자리의 농도 (개수/m²), [A_ad]는 표면의 A 농도 (분자/m², 점유된 자리의 농도), 그리고 k_ad와 k_d는 위의 반응에서 정방향 흡착 반응과 역방향 탈착 반응의 상수이다.

평형 상태에서 흡착 속도는 탈착 속도와 같다. r_ad = r_d로 설정하고 정리하면 다음과 같다.

${\displaystyle {\frac {[A_{\text{ad}}]}{p_{A}[S]}}={\frac {k_{\text{ad}}}{k_{\text{d}}}}=K_{\text{eq}}^{A}.}$

자리 농도는 전체 표면을 덮는 총 자리 수(S₀)를 흡착제 면적(a)으로 나누어 얻는다.

${\displaystyle [S_{0}]=S_{0}/a.}$

그런 다음 자유 자리 농도 [S]와 점유된 자리 농도를 합하여 모든 자리의 농도를 계산할 수 있다.

${\displaystyle [S_{0}]=[S]+[A_{\text{ad}}].}$

이를 평형 방정식과 결합하면 다음과 같다.

${\displaystyle [S_{0}]={\frac {[A_{\text{ad}}]}{K_{\text{eq}}^{A}p_{A}}}+[A_{\text{ad}}]={\frac {1+K_{\text{eq}}^{A}p_{A}}{K_{\text{eq}}^{A}p_{A}}}[A_{\text{ad}}].}$

이제 A로 덮인 표면 자리의 분율을 다음과 같이 정의한다.

${\displaystyle \theta _{A}={\frac {[A_{\text{ad}}]}{[S_{0}]}}.}$

이를 자리 균형과 평형을 결합한 이전 방정식에 적용하면 랭뮤어 흡착 등온식이 얻어진다.

${\displaystyle \theta _{A}={\frac {K_{\text{eq}}^{A}p_{A}}{1+K_{\text{eq}}^{A}p_{A}}}.}$

열역학적 유도

응축상(용액)에서 고체 표면으로의 흡착은 용매(A)와 용질(B)이 결합 자리를 차지하기 위해 경쟁하는 과정이다. 열역학적 평형은 다음과 같이 설명된다.

용매 (결합) + 용질 (자유) ↔ 용매 (자유) + 용질 (결합).

용매를 아래첨자 "1"로, 용질을 "2"로, 결합 상태를 위첨자 "s"(표면/결합)로, 자유 상태를 "b"(용액 벌크/자유)로 지정하면, 평형 상수는 생성물 활성도의 반응물 활성도에 대한 비율로 작성될 수 있다.

${\displaystyle K={\frac {a_{1}^{\text{b}}\times a_{2}^{\text{s}}}{a_{2}^{\text{b}}\times a_{1}^{\text{s}}}}.}$

묽은 용액의 경우 벌크 용액의 용매 활성도 ${\displaystyle a_{1}^{\text{b}}\simeq 1,}$ 이고, 표면에서 활성도 계수(${\displaystyle \gamma }$)도 이상적이라고 가정한다. 따라서 ${\displaystyle a_{2}^{\text{s}}=X_{2}^{\text{s}}=\theta ,}$ ${\displaystyle a_{1}^{\text{s}}=X_{1}^{\text{s}},}$, 그리고 ${\displaystyle X_{1}^{\text{s}}+X_{2}^{\text{s}}=1,}$ 이다. 여기서 ${\displaystyle X_{i}}$는 몰분율이다. 평형 상수를 다시 쓰고 ${\displaystyle \theta }$에 대해 풀면 다음과 같다.

${\displaystyle \theta ={\frac {Ka_{2}^{\text{b}}}{1+Ka_{2}^{\text{b}}}}.}$

용질 흡착물의 농도는 활성도 계수 대신 사용될 수 있다. 그러나 이 경우 평형 상수는 더 이상 무차원이 아니며 역 농도 단위를 갖게 된다. 랭뮤어 모델의 동역학적 유도와 열역학적 유도 간의 차이점은 열역학적 유도는 활성도를 시작점으로 사용하는 반면 동역학적 유도는 반응 속도를 사용한다는 것이다. 열역학적 유도는 흡착물의 결합 및 자유 상태에서 활성도 계수를 포함할 수 있도록 한다. 열역학적 유도는 일반적으로 "랭뮤어 유사 방정식"이라고 불린다.^[6][7]

통계역학적 유도

이 유도^[8][9]는 1925년에 폴머와 마너트(Volmer and Mahnert)^[10]가 처음 제공한 통계역학에 기반을 두고 있다. 바른틀 앙상블에서 표면에 흡착된 유한한 수의 흡착물에 대한 분배 함수는 다음과 같이 주어진다.

${\displaystyle Z(N_{A})=\left[\zeta _{L}^{N_{A}}{\frac {N_{S}!}{(N_{S}-N_{A})!}}\right]{\frac {1}{N_{A}!}},}$

여기서 ${\displaystyle \zeta _{L}}$은 단일 흡착 분자의 분배 함수이고, ${\displaystyle N_{S}}$는 흡착 자리의 수(점유 및 비점유 모두 포함), 그리고 ${\displaystyle N_{A}}$는 흡착된 분자의 수로, ${\displaystyle N_{S}}$보다 작거나 같아야 한다. 괄호 안의 항은 개별 분배 함수의 곱을 취하여 ${\displaystyle N_{A}}$ 흡착된 분자의 총 분배 함수를 제공한다(부분계의 분배 함수 참조). ${\displaystyle 1/N_{A}!}$ 인자는 흡착물의 구별 불가능한 특성으로 인해 발생하는 중복 계산을 설명한다. 거대 바른틀 분배 함수는 다음과 같이 주어진다.

${\displaystyle {\mathcal {Z}}(\mu _{A})=\sum _{N_{A}=0}^{N_{S}}\exp \left({\frac {N_{A}\mu _{A}}{k_{\text{B}}T}}\right){\frac {\zeta _{L}^{N_{A}}}{N_{A}!}}\,{\frac {N_{S}!}{(N_{S}-N_{A})!}}.}$

${\displaystyle \mu _{A}}$는 흡착 분자의 화학 퍼텐셜이다. 이것은 이항 정리의 형태를 가지고 있으므로 합계는 다음으로 축소된다.

${\displaystyle {\mathcal {Z}}(\mu _{A})=(1+x)^{N_{S}},}$

여기서 ${\displaystyle x=\zeta _{L}\exp \left({\frac {\mu _{A}}{k_{\rm {B}}T}}\right).}$

거대 바른틀 퍼텐셜은

${\displaystyle \Omega =-k_{\rm {B}}T\ln({\mathcal {Z}})=-k_{\rm {B}}TN_{S}\ln(1+x),}$

이를 바탕으로 점유된 자리의 평균 수가 계산된다.

${\displaystyle \langle N_{A}\rangle =-\left({\frac {\partial \Omega }{\partial \mu _{A}}}\right)_{T,{\text{area}}},}$

이는 덮음률을 제공한다.

${\displaystyle \theta _{A}={\frac {\langle N_{A}\rangle }{N_{S}}}={\frac {x}{1+x}}.}$

이제 시스템이 평형 상태에 있다는 조건을 적용하면, 즉 흡착 분자의 화학 퍼텐셜이 기체상 분자의 화학 퍼텐셜과 같다는 조건에서 다음과 같다.

흡착물의 부분 압력에 대한 표면 덮음률 θ_A = P/(P + P₀)의 예시 그래프. P₀ = 100 mTorr. 그래프는 P가 P₀보다 높을 때 표면 덮음률이 평탄해지는 것을 보여준다.

${\displaystyle \mu _{A}=\mu _{\text{g}},}$

이상 기체의 화학 퍼텐셜은 다음과 같다.

${\displaystyle \mu _{\text{g}}=\left({\frac {\partial A_{\text{g}}}{\partial N}}\right)_{T,V}}$

여기서 ${\displaystyle A_{g}=-k_{\rm {B}}T\ln Z_{g}}$는 이상 기체의 헬름홀츠 자유 에너지이며, 그 분배 함수는 다음과 같다.

${\displaystyle Z_{g}={\frac {q^{N}}{N!}}.}$

${\displaystyle q}$는 부피 ${\displaystyle V}$ 내 단일 입자의 분배 함수이다(여기서는 병진 자유도만 고려).

${\displaystyle q=V\left({\frac {2\pi mk_{\rm {B}}T}{h^{2}}}\right)^{3/2}.}$

따라서 스털링 근사를 사용하여 ${\displaystyle \mu _{g}=-k_{\rm {B}}T\ln(q/N)}$이다.

${\displaystyle \mu _{g}}$를 ${\displaystyle x}$의 표현식에 대입하면 다음과 같다.

${\displaystyle {\frac {\theta _{A}}{1-\theta _{A}}}=x=\zeta _{L}{\frac {N}{q}}}$

이는 덮음률을 제공한다.

${\displaystyle \theta _{A}={\frac {\zeta _{L}/(q/N)}{1+\zeta _{L}/(q/N)}}}$

다음과 같이 정의하여

${\displaystyle P_{0}={\frac {k_{\text{B}}T}{\zeta _{L}}}\left({\frac {2\pi mk_{\text{B}}T}{h^{2}}}\right)^{3/2}}$

그리고 ${\displaystyle PV=Nk_{\rm {B}}T}$ 항등식을 사용하면 최종적으로 다음과 같다.

${\displaystyle \theta _{A}={\frac {P}{P+P_{0}}}.}$

이것은 옆 그림에 그려져 있으며, 표면 덮음률이 흡착물 부분 압력에 따라 상당히 빠르게 증가하지만, P가 P₀에 도달한 후에는 평탄해지는 것을 보여준다.

경쟁적 흡착

이전 유도에서는 표면에 흡착되는 종이 A 하나뿐이라고 가정했다. 이 섹션^[11]에서는 시스템에 두 가지 다른 흡착물이 존재하는 경우를 고려한다. 동일한 흡착 자리를 놓고 경쟁하는 두 가지 종 A와 B를 고려하자. 여기서 다음 가설이 유효하다고 가정한다.

1. 모든 자리는 동일하다.
2. 각 자리는 최대 하나의 A 분자 또는 하나의 B 분자를 수용할 수 있지만, 동시에 둘 다는 아니다.
3. 인접한 자리의 흡착물 분자 간에는 상호작용이 없다.

동역학적 고려 사항을 사용하여 유도된 바와 같이, A와 B 모두에 대한 평형 상수는 다음과 같이 주어진다.

${\displaystyle {\frac {[A_{\text{ad}}]}{p_{A}\,[S]}}=K_{\text{eq}}^{A}}$

그리고

${\displaystyle {\frac {[B_{\text{ad}}]}{p_{B}\,[S]}}=K_{\text{eq}}^{B}.}$

자리 균형은 총 자리 농도 [S₀]가 자유 자리, A가 점유한 자리 및 B가 점유한 자리의 합과 같다고 말한다.

${\displaystyle [S_{0}]=[S]+[A_{\text{ad}}]+[B_{\text{ad}}].}$

평형 방정식을 삽입하고 단일 종 흡착에서 했던 것과 같은 방식으로 재정렬하면 θ_A와 θ_B 모두에 대한 유사한 표현을 얻는다.

${\displaystyle \theta _{A}={\frac {K_{\text{eq}}^{A}\,p_{A}}{1+K_{\text{eq}}^{A}\,p_{A}+K_{\text{eq}}^{B}\,p_{B}}},}$

${\displaystyle \theta _{B}={\frac {K_{\text{eq}}^{B}\,p_{B}}{1+K_{\text{eq}}^{A}\,p_{A}+K_{\text{eq}}^{B}\,p_{B}}}.}$

해리성 흡착

특히 중요한 또 다른 경우는 분자 D₂가 흡착 시 두 개의 원자로 해리되는 경우이다.^[11] 여기서 다음 가정이 유효하다고 간주된다.

1. D₂는 흡착 시 두 개의 D 분자로 완전히 해리된다.
2. D 원자는 고체 표면의 별개의 자리에 흡착된 후 이동하여 평형을 이룬다.
3. 모든 자리는 동일하다.
4. 각 자리는 최대 하나의 D 원자만 수용할 수 있다.
5. 인접한 자리의 흡착물 분자 간에는 상호작용이 없다.

유사한 동역학적 고려 사항을 사용하면 다음과 같다.

${\displaystyle {\frac {[D_{\text{ad}}]}{p_{D_{2}}^{1/2}[S]}}=K_{\text{eq}}^{D}.}$

p_D2에 붙은 1/2 지수는 기체상 분자 하나가 두 개의 흡착종을 생성하기 때문에 발생한다. 위에서 했던 것처럼 자리 균형을 적용하면 다음과 같다.

${\displaystyle \theta _{D}={\frac {(K_{\text{eq}}^{D}\,p_{D_{2}})^{1/2}}{1+(K_{\text{eq}}^{D}\,p_{D_{2}})^{1/2}}}.}$

엔트로피 고려 사항

표면으로 흡착에 의한 랭뮤어 단일층의 형성은 분자 시스템의 엔트로피를 극적으로 감소시킨다.

엔트로피 감소를 찾기 위해, 흡착 상태에 있을 때 분자의 엔트로피를 찾는다.^[12]

${\displaystyle S=S_{\text{configurational}}+S_{\text{vibrational}},}$

${\displaystyle S_{\text{conf}}=k_{\rm {B}}\ln \Omega _{\text{conf}},}$

${\displaystyle \Omega _{\text{conf}}={\frac {N_{S}!}{N!(N_{S}-N)!}}.}$

스털링 근사를 사용하면 다음과 같다.

${\displaystyle \ln N!\approx N\ln N-N,}$

${\displaystyle S_{\text{conf}}/k_{\rm {B}}\approx -\theta _{A}\ln(\theta _{A})-(1-\theta _{A})\ln(1-\theta _{A}).}$

반면에 이상 기체 분자의 엔트로피는 다음과 같다.

${\displaystyle {\frac {S_{\text{gas}}}{Nk_{\text{B}}}}=\ln \left({\frac {k_{\text{B}}T}{P\lambda ^{3}}}\right)+5/2,}$

여기서 ${\displaystyle \lambda }$는 기체 분자의 열 드 브로이 파장이다.

모델의 한계

랭뮤어 흡착 모델은 주로 흡착제의 표면 거칠기를 설명하지 못하기 때문에 많은 경우에 크게 벗어난다. 거친 불균일 표면에는 흡착을 위한 여러 유형의 자리가 있으며, 흡착열과 같은 일부 매개변수는 자리마다 다르다. 또한, 비표면적은 규모에 의존하는 양이므로, 이 매개변수에 대한 단일한 참값은 존재하지 않는다.^[1] 따라서 대체 프로브 분자를 사용하면 종종 다른 표면적 수치를 얻게 되어 비교가 어렵다.

이 모델은 또한 흡착물-흡착물 상호작용을 무시한다. 실험적으로 흡착열 데이터에서 흡착물-흡착물 상호작용의 명확한 증거가 있다. 흡착물-흡착물 상호작용에는 직접 상호작용과 간접 상호작용의 두 가지 종류가 있다. 직접 상호작용은 인접한 흡착된 분자들 사이에서 발생하며, 이는 다른 흡착물 분자 근처에서 흡착하는 것을 더 유리하게 만들거나 덜 유리하게 만들 수 있으며, 고피복도 거동에 큰 영향을 미친다. 간접 상호작용에서는 흡착물이 흡착된 자리 주변의 표면을 변경하여 근처의 다른 흡착물 분자의 흡착에 영향을 미친다.

수정된 모델

수정된 모델들은 위 섹션에서 언급된 표면 거칠기, 불균일성 및 흡착물-흡착물 상호작용과 같은 문제점을 설명하려고 시도한다.

두 가지 메커니즘 랭뮤어 유사 방정식 (TMLLE)

두 자리 랭뮤어 방정식으로도 알려져 있다. 이 방정식은 하나 이상의 다른 유형의 흡착 자리에 대한 흡착물 하나를 설명한다. 각 결합 자리는 각 결합 자리 유형에서의 흡착이 나머지로부터 독립적인 한, 자체 랭뮤어 식으로 설명될 수 있다.

${\displaystyle q_{\text{total}}={\frac {q_{1}^{\text{max}}K_{1}a_{2}^{\text{b}}}{1+K_{1}a_{2}^{\text{b}}}}+{\frac {q_{2}^{\text{max}}K_{2}a_{2}^{\text{b}}}{1+K_{2}a_{2}^{\text{b}}}}+\dots ,}$

여기서

${\displaystyle q_{\text{total}}}$ – 주어진 흡착물 농도에서 총 흡착량,

${\displaystyle q_{1}^{\text{max}}}$ – 유형 1 자리의 최대 용량,

${\displaystyle q_{2}^{\text{max}}}$ – 유형 2 자리의 최대 용량,

${\displaystyle K_{1}}$ – 유형 1 자리의 평형(친화도) 상수,

${\displaystyle K_{2}}$ – 유형 2 자리의 평형(친화도) 상수,

${\displaystyle a_{2}^{\text{b}}}$ – 평형 상태에서 용액 내 흡착물 활성도

이 방정식은 일부 약물 분자의 활성탄 흡착에 잘 적용된다. 이 경우 일부 흡착물 분자는 수소 결합으로 상호작용하고 다른 분자는 소수성 효과에 의해 표면의 다른 부분과 상호작용한다. 이 방정식은 소수성 효과(엔트로피 구동 흡착이라고도 함)를 설명하기 위해 수정되었다.^[13]

${\displaystyle q_{\text{total}}={\frac {q_{1}^{\text{max}}K_{1}a_{2}^{\text{b}}}{1+K_{1}a_{2}^{\text{b}}}}+q_{\text{HB}}.}$

소수성 효과는 농도와 무관하며, ${\displaystyle K_{2}a_{2}^{\text{b}}\gg 1.}$ 이다. 따라서 소수성 상호작용에 대한 흡착제의 용량 ${\displaystyle q_{\text{HB}}}$는 실험 데이터에 맞춰 얻을 수 있다. 엔트로피 구동 흡착은 흡착물에 의해 벌크 물 분자의 병진 운동이 제한되는 것으로부터 발생하며, 이는 흡착 시 완화된다.

프룬들리히 흡착 등온식

 이 부분의 본문은 프룬들리히 방정식입니다.

프룬들리히 등온식은 거친 표면에 대한 가장 중요한 다중 자리 흡착 등온식이다.

${\displaystyle \theta _{A}=\alpha _{F}p^{C_{\text{F}}},}$

여기서 α_F와 C_F는 피팅 매개변수이다.^[14] 이 방정식은 흡착 데이터의 로그-로그 플롯을 만들면 데이터가 직선에 맞을 것임을 의미한다. 프룬들리히 등온식은 두 개의 매개변수를 가지는 반면 랭뮤어 방정식은 하나만 가진다. 결과적으로 랭뮤어 등온식보다 거친 표면의 데이터에 더 잘 맞는 경우가 많다. 그러나 프룬들리히 방정식은 고유하지 않다. 따라서 데이터 포인트가 잘 맞는다고 해서 표면이 불균일하다는 충분한 증거를 제공하지는 않는다. 표면의 불균일성은 열량계로 확인할 수 있다. 균일한 표면(또는 균일한 흡착(단일 자리)을 보이는 불균일 표면)은 점유된 자리의 분율에 따라 일정한 흡착 ${\displaystyle \Delta H}$를 가진다. 반면에 불균일 흡착제(다중 자리)는 자리 점유에 따라 가변적인 흡착 ${\displaystyle \Delta H}$를 가진다. 흡착물 압력(또는 농도)이 낮으면 부분 점유율이 작고 결과적으로 저에너지 자리만 점유된다. 이는 가장 안정적이기 때문이다. 압력이 증가하면 고에너지 자리도 점유되어 흡착 ${\displaystyle \Delta H}$가 작아지는데, 이는 흡착이 발열 과정이기 때문이다.^[15]

관련된 방정식은 토스(Toth) 방정식이다. 랭뮤어 방정식을 재배열하면 다음과 같다.

${\displaystyle \theta _{A}={\frac {p_{A}}{{\frac {1}{K_{\text{eq}}^{A}}}+p_{A}}}.}$

J. 토스(Toth)^[16]는 두 매개변수 α_T0와 C_T0를 추가하여 이 방정식을 수정하여 토스 방정식을 만들었다.

${\displaystyle \theta ^{C_{T_{0}}}={\frac {\alpha _{T_{0}}p_{A}^{C_{T_{0}}}}{{\frac {1}{K_{\text{eq}}^{A}}}+p_{A}^{C_{T_{0}}}}}.}$

BET 방정식

 이 부분의 본문은 BET 이론입니다.

브루나워, 에밋, 텔러(BET)의 다층 흡착 모델. 즉, 하나, 둘, 셋 등의 흡착물 분자로 덮인 자리의 무작위 분포이다.

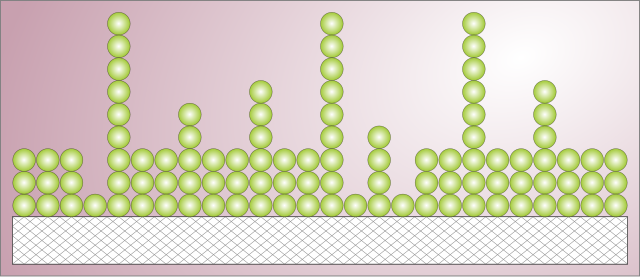
브루나워, 에밋, 텔러(BET)^[17]는 다층 흡착에 대한 첫 번째 등온식을 유도했다. 이는 옆 그림에서 설명된 바와 같이 비어 있거나 단일층, 두 층 등으로 덮인 자리의 무작위 분포를 가정한다. 이 모델의 주요 방정식은 다음과 같다.

${\displaystyle {\frac {[A]}{S_{0}}}={\frac {c_{B}x_{B}}{(1-x_{B})[1+(c_{B}-1)x_{B}]}},}$

여기서

${\displaystyle x_{B}=p_{A}K_{m},\quad c_{B}={\frac {K_{1}}{K_{m}}},}$

그리고 [A]는 표면의 총 분자 농도이며, 다음으로 주어진다.

${\displaystyle [A]=\sum _{i=1}^{\infty }i[A]_{i}=\sum _{i=1}^{\infty }iK_{1}K_{m}^{i-1}p_{A}^{i}[A]_{0},}$

여기서

${\displaystyle K_{i}={\frac {[A]_{i}}{p_{A}[A]_{i-1}}},}$

여기서 [A]₀는 빈 자리의 수이고, [A]_i는 i개의 분자로 덮인 표면 자리의 수이다.

고체에 대한 이성분 액체의 흡착

이 섹션은 흡착물이 액상이고 이성분 혼합물일 때의 표면 덮음률을 설명한다.^[18]

이상적인 두 상에 대해^{명확화 필요} – 측면 상호작용이 없고, 균일한 표면 – 에서 고체 표면과 접촉하는 이성분 액체 시스템의 표면상 구성은 고전적인 에버렛 등온 방정식 (랭뮤어 방정식의 간단한 아날로그)으로 주어지며, 여기서 성분들은 서로 교환 가능하다 (즉, "1"은 "2"로 교환될 수 있다) 방정식 형태의 변경 없이:

${\displaystyle x_{1}^{s}={\frac {Kx_{1}^{l}}{1+(K-1)x_{1}^{l}}},}$

여기서 다성분 시스템의 일반적인 정의는 다음과 같이 유효하다.

${\displaystyle \sum _{i=1}^{k}x_{i}^{s}=1,\quad \sum _{i=1}^{k}x_{i}^{l}=1.}$

간단한 재배열을 통해 다음을 얻는다.

${\displaystyle x_{1}^{s}={\frac {K[x_{1}^{l}/(1-x_{1}^{l})]}{1+K[x_{1}^{l}/(1-x_{1}^{l})]}}.}$

이 방정식은 성분 "1"과 "2"의 경쟁을 설명한다.

같이 보기

• 힐 방정식 (생화학)
• 미카엘리스-멘텐 반응속도론: 동일한 수학적 형태의 방정식
• 모노드식: 동일한 수학적 형태의 방정식
• 표면 반응