버터워스 필터

버터워스 필터(Butterworth filter)는 통과대역에서 최대한 평탄한 주파수 응답을 가지도록 설계된 신호 처리 필터의 한 종류이다. 최대 평탄 필터(maximally flat magnitude filter)라고도 불린다. 1930년 영국의 엔지니어이자 물리학자인 스티븐 버터워스가 그의 논문 "On the Theory of Filter Amplifiers"에서 처음 기술했다.^[1]

원본 논문

버터워스는 '불가능하다'고 여겨지는 매우 복잡한 수학적 문제를 해결하는 것으로 명성이 높았다. 당시 필터 설계는 당시 사용되던 이론의 한계 때문에 상당한 설계자의 경험이 필요했다. 버터워스 필터는 출판 후 30년 이상 일반적인 사용이 이루어지지 않았다. 버터워스는 다음과 같이 말했다.

“

이상적인 전기 필터는 원치 않는 주파수를 완전히 차단할 뿐만 아니라 원하는 주파수에 대해 균일한 감도를 가져야 한다.

”

이러한 이상적인 필터는 달성할 수 없지만, 버터워스는 적절한 값을 가진 더 많은 수의 필터 소자를 사용하면 점진적으로 더 나은 근사치가 얻어진다는 것을 보여주었다. 당시 필터는 통과대역에서 상당한 잔물결(ripple)을 생성했고, 부품 값의 선택은 상호 작용이 매우 심했다. 버터워스는 로우패스 필터를 설계할 수 있음을 보여주었는데, 이 필터의 이득은 주파수 함수(즉, 주파수 응답의 크기)로서 다음과 같다.

${\displaystyle G(\omega )={\frac {1}{\sqrt {1+{\omega }^{2n}}}},}$

여기서 ${\displaystyle \omega }$는 초당 라디안 단위의 각진동수이고 ${\displaystyle n}$은 필터의 극의 수로, 수동 필터에서는 반응성 소자의 수와 같다. 차단 주파수(대략 -3 dB 또는 전압 이득이 1/√2 ≈ 0.7071인 반파력점)는 ${\displaystyle \omega }$ = 1 라디안/초로 정규화된다. 버터워스는 그의 논문에서 짝수 개의 극을 가진 필터만 다루었지만, 홀수 차수 필터는 짝수 차수 필터의 출력에 단극 필터를 추가하여 만들 수 있다. 그는 2극 필터를 진공관 앰프로 분리하여 고차 필터를 만들었다. 그의 논문에 있는 원래 그래프에서 2, 4, 6, 8, 10극 필터의 주파수 응답 플롯은 A, B, C, D, E로 표시되어 있다.

버터워스는 2극 및 4극 필터에 대한 방정식을 풀어 4극 필터가 진공관 앰프에 의해 분리될 때 어떻게 캐스케이드될 수 있는지 보여주었고, 이로써 유도자 손실에도 불구하고 고차 필터의 구성을 가능하게 했다. 1930년에는 몰리퍼멀로이와 같은 저손실 코어 재료가 발견되지 않았으며, 공심 오디오 유도자는 상당히 손실이 많았다. 버터워스는 유도자의 권선 저항을 보상하기 위해 필터의 부품 값을 조정하는 것이 가능하다는 것을 발견했다.

그는 플러그인 단자가 있는 직경 1.25인치, 길이 3인치의 코일 형태를 사용했다. 관련 콘덴서와 저항은 권선된 코일 형태 안에 포함되었다. 코일은 플레이트 부하 저항의 일부를 형성했다. 진공관 당 두 개의 극이 사용되었고, 후속 관의 격자에는 RC 결합이 사용되었다.

버터워스는 또한 기본적인 로우패스 필터가 로우패스, 하이패스, 대역 통과, 대역 차단 기능을 제공하도록 수정될 수 있다는 것을 보여주었다.

개요

1차 로우패스 필터의 보데 선도

버터워스 필터의 주파수 응답은 통과대역에서 최대 평탄(즉, 잔물결이 없음)하며 저지대역에서 0으로 롤오프한다.^[2] 로그 보데 선도에서 보면 응답은 음의 무한대를 향해 선형적으로 기울어진다. 1차 필터의 응답은 옥타브당 -6 dB(decade당 -20 dB)로 롤오프한다(모든 1차 로우패스 필터는 동일한 정규화된 주파수 응답을 가진다). 2차 필터는 옥타브당 -12 dB, 3차 필터는 옥타브당 -18 dB 등으로 감소한다. 버터워스 필터는 통과대역 및 저지대역에 비단조 잔물결이 있는 다른 필터 유형과 달리 ${\displaystyle \omega }$에 대해 단조적으로 변화하는 크기 함수를 갖는다.

체비셰프 I/II형 필터 또는 타원 필터와 비교할 때 버터워스 필터는 롤오프가 더 느리므로 특정 저지대역 사양을 구현하기 위해 더 높은 차수가 필요하지만, 버터워스 필터는 체비셰프 I/II형 필터 및 타원 필터보다 통과대역에서 더 선형적인 위상 응답을 갖는다.

예시

오른쪽 그림에 표시된 3차 로우패스 버터워스 필터 설계의 전달 함수는 다음과 같다.

${\displaystyle {\frac {V_{o}(s)}{V_{i}(s)}}={\frac {R_{4}}{s^{3}(L_{1}C_{2}L_{3})+s^{2}(L_{1}C_{2}R_{4})+s(L_{1}+L_{3})+R_{4}}}}$

3차 로우패스 필터(카우어 토폴로지). 필터는 (예를 들어) ${\displaystyle C_{2}}$=4/3 F, ${\displaystyle R_{4}}$=1 Ω, ${\displaystyle L_{1}}$=3/2 H, ${\displaystyle L_{3}}$=1/2 H일 때 차단 주파수 ${\displaystyle \omega _{c}}$=1을 갖는 버터워스 필터가 된다.

버터워스 필터의 간단한 예는 오른쪽 그림에 표시된 3차 로우패스 설계로, ${\displaystyle C_{2}}$ = 4/3 F, ${\displaystyle R_{4}}$ = 1 Ω, ${\displaystyle L_{1}}$ = 3/2 H, ${\displaystyle L_{3}}$ = 1/2 H이다.^[3] 콘덴서 ${\displaystyle C}$의 온저항을 ${\displaystyle 1/(Cs)}$로, 유도자 ${\displaystyle L}$의 온저항을 ${\displaystyle Ls}$로 취하면(여기서 ${\displaystyle s=\sigma +j\omega }$는 복소 주파수), 회로 방정식은 이 장치에 대한 전달 함수를 산출한다.

${\displaystyle H(s)={\frac {V_{o}(s)}{V_{i}(s)}}={\frac {1}{1+2s+2s^{2}+s^{3}}}.}$

주파수 응답의 크기(이득) ${\displaystyle G(\omega )}$는 다음으로 주어진다.

${\displaystyle G(\omega )=|H(j\omega )|={\frac {1}{\sqrt {1+\omega ^{6}}}},}$

다음에서 얻어진다.

${\displaystyle G^{2}(\omega )=|H(j\omega )|^{2}=H(j\omega )\cdot H^{*}(j\omega )={\frac {1}{1+\omega ^{6}}},}$

그리고 위상은 다음으로 주어진다.

${\displaystyle \Phi (\omega )=\arg(H(j\omega )).\!}$

${\displaystyle \omega _{c}=1}$을 갖는 3차 버터워스 필터의 이득 및 군지연

군지연은 각주파수에 대한 위상 편이의 음수 미분으로 정의되며, 서로 다른 주파수에 대한 위상 차이에 의해 신호에 도입되는 왜곡의 측정값이다. 이 필터의 이득과 지연은 왼쪽 그래프에 플롯되어 있다. 이득 곡선에는 통과대역이나 저지대역 모두에 잔물결이 없다.

전달 함수 ${\displaystyle H(s)}$의 절댓값의 로그는 오른쪽 두 번째 그래프에서 복소 주파수 공간에 플롯되어 있다. 이 함수는 복소 주파수 평면의 왼쪽 절반에 있는 세 개의 극으로 정의된다.

${\displaystyle \omega _{c}}$=1을 갖는 3차 버터워스 필터에 대한 복소 주파수 공간에서 전달 함수 ${\displaystyle H(s)}$의 로그 밀도 플롯. 세 개의 극은 왼쪽 절반 평면에서 단위 반경의 원 위에 놓여 있다.

이들은 실수 ${\displaystyle s}$ 축에 대해 대칭적으로 단위 반경의 원 위에 배열되어 있다. 이득 함수는 원을 완성하기 위해 오른쪽 절반 평면에 세 개의 극을 더 갖게 된다.

각 유도자를 콘덴서로, 각 콘덴서를 유도자로 교체하여 하이패스 버터워스 필터를 얻을 수 있다.

대역 통과 버터워스 필터는 각 유도자와 직렬로 콘덴서를 놓고 각 콘덴서와 병렬로 유도자를 놓아 공진 회로를 형성함으로써 얻을 수 있다. 각 새 부품의 값은 관심 주파수에서 이전 부품과 공진하도록 선택해야 한다.

대역 차단 버터워스 필터는 각 유도자와 병렬로 콘덴서를 놓고 각 콘덴서와 직렬로 유도자를 놓아 공진 회로를 형성함으로써 얻을 수 있다. 각 새 부품의 값은 차단하려는 주파수에서 이전 부품과 공진하도록 선택해야 한다.

전달 함수

차단 주파수 ${\displaystyle \omega _{c}=1}$을 갖는 1차부터 5차까지의 버터워스 로우패스 필터 이득 플롯. 기울기는 필터 차수 ${\displaystyle n}$일 때 20${\displaystyle n}$ dB/decade임을 유의하라.

모든 필터와 마찬가지로 일반적인 원형 필터는 로우패스 필터이며, 하이패스 필터로 수정하거나 다른 필터와 직렬로 배치하여 대역 통과 및 대역 차단 필터, 그리고 이들의 고차 버전을 형성할 수 있다.

${\displaystyle n}$차 버터워스 로우패스 필터의 이득 ${\displaystyle G(\omega )}$는 전달 함수 ${\displaystyle H(s)}$에 대해 다음과 같이 주어진다.

${\displaystyle G^{2}(\omega )=\left|H(j\omega )\right|^{2}={\frac {{G_{0}}^{2}}{1+\left({\frac {\omega }{\omega _{c}}}\right)^{2n}}}}$

여기서 ${\displaystyle n}$은 필터의 차수이고, ${\displaystyle \omega _{c}}$는 차단 주파수(대략 -3 dB 주파수)이며, ${\displaystyle G_{0}}$는 DC 이득(제로 주파수에서의 이득)이다.

${\displaystyle n}$이 무한대로 접근함에 따라 이득은 사각 함수가 되고 ${\displaystyle \omega _{c}}$ 미만의 주파수는 이득 ${\displaystyle G_{0}}$으로 통과되는 반면, ${\displaystyle \omega _{c}}$ 이상의 주파수는 억제됨을 알 수 있다. ${\displaystyle n}$ 값이 작을수록 차단은 덜 날카로워진다.

우리는 라플라스 변환에서 ${\displaystyle s=\sigma +j\omega }$인 전달 함수 ${\displaystyle H(s)}$를 결정하고자 한다. ${\displaystyle \left|H(s)\right|^{2}=H(s){\overline {H(s)}}}$이고, ${\displaystyle s=j\omega }$에서 라플라스 변환의 일반적인 속성으로 ${\displaystyle H(-j\omega )={\overline {H(j\omega )}}}$이므로, 다음과 같이 ${\displaystyle H(s)}$를 선택하면:

${\displaystyle H(s)H(-s)={\frac {{G_{0}}^{2}}{1+\left({\frac {-s^{2}}{\omega _{c}^{2}}}\right)^{n}}},}$

그러면 ${\displaystyle s=j\omega }$에서 버터워스 필터의 주파수 응답을 얻게 된다.

이 표현식의 ${\displaystyle n}$개 극은 반경 ${\displaystyle \omega _{c}}$의 원 위에 등간격으로 놓여 있으며 음의 실수 축에 대해 대칭이다. 따라서 안정성을 위해 전달 함수 ${\displaystyle H(s)}$는 ${\displaystyle s}$의 음의 실수 절반 평면에 있는 극만 포함하도록 선택된다. ${\displaystyle k}$번째 극은 다음과 같이 지정된다.

${\displaystyle -{\frac {s_{k}^{2}}{\omega _{c}^{2}}}=(-1)^{\frac {1}{n}}=e^{\frac {j(2k-1)\pi }{n}}\qquad k=1,2,3,\ldots ,n}$

따라서

${\displaystyle s_{k}=\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}\qquad k=1,2,3,\ldots ,n.}$

전달(또는 시스템) 함수는 이러한 극을 사용하여 다음과 같이 쓸 수 있다.

${\displaystyle H(s)=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-s_{k}}}=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}}}}$.

여기서 ${\displaystyle \textstyle {\prod }}$는 수열의 곱 연산자이다. 분모는 ${\displaystyle s}$에 대한 버터워스 다항식이다.

정규화된 버터워스 다항식

버터워스 다항식은 위와 같이 복소 형태로 쓸 수 있지만, 일반적으로 ${\displaystyle s_{1}}$과 ${\displaystyle s_{n}}$과 같이 복소 공액인 극 쌍을 곱하여 실수 계수로 쓰인다. 다항식은 ${\displaystyle \omega _{c}=1}$로 설정하여 정규화된다. 그러면 정규화된 버터워스 다항식은 일반적인 곱 형태로 다음을 갖는다.

${\displaystyle B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]\qquad n={\text{even}}}$

${\displaystyle B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]\qquad n={\text{odd}}.}$

1차부터 10차까지의 버터워스 다항식의 인자는 다음 표에 나와 있다(소수점 여섯 자리까지).

n 버터워스 다항식 ${\displaystyle B_{n}(s)}$의 인자 1 ${\displaystyle (s+1)}$ 2 ${\displaystyle (s^{2}+1.414214s+1)}$ 3 ${\displaystyle (s+1)(s^{2}+s+1)}$ 4 ${\displaystyle (s^{2}+0.765367s+1)(s^{2}+1.847759s+1)}$ 5 ${\displaystyle (s+1)(s^{2}+0.618034s+1)(s^{2}+1.618034s+1)}$ 6 ${\displaystyle (s^{2}+0.517638s+1)(s^{2}+1.414214s+1)(s^{2}+1.931852s+1)}$ 7 ${\displaystyle (s+1)(s^{2}+0.445042s+1)(s^{2}+1.246980s+1)(s^{2}+1.801938s+1)}$ 8 ${\displaystyle (s^{2}+0.390181s+1)(s^{2}+1.111140s+1)(s^{2}+1.662939s+1)(s^{2}+1.961571s+1)}$ 9 ${\displaystyle (s+1)(s^{2}+0.347296s+1)(s^{2}+s+1)(s^{2}+1.532089s+1)(s^{2}+1.879385s+1)}$ 10 ${\displaystyle (s^{2}+0.312869s+1)(s^{2}+0.907981s+1)(s^{2}+1.414214s+1)(s^{2}+1.782013s+1)(s^{2}+1.975377s+1)}$

1차부터 6차까지의 버터워스 다항식의 인자는 다음 표에 나와 있다(정확한 값).

n 버터워스 다항식 ${\displaystyle B_{n}(s)}$의 인자 1 ${\displaystyle (s+1)}$ 2 ${\displaystyle (s^{2}+{\sqrt {2}}s+1)}$ 3 ${\displaystyle (s+1)(s^{2}+s+1)}$ 4 ${\displaystyle (s^{2}+{\sqrt {2-{\sqrt {2}}}}s+1)(s^{2}+{\sqrt {2+{\sqrt {2}}}}s+1)}$ 5 ${\displaystyle (s+1)(s^{2}+\varphi ^{-1}s+1)(s^{2}+\varphi s+1)}$ 6 ${\displaystyle (s^{2}+{\sqrt {2-{\sqrt {3}}}}s+1)(s^{2}+{\sqrt {2}}s+1)(s^{2}+{\sqrt {2+{\sqrt {3}}}}s+1)}$

여기서 그리스 문자 phi(${\displaystyle \varphi }$ 또는 ${\displaystyle \phi }$)는 황금비를 나타낸다. 이는 이차 방정식 ${\displaystyle x^{2}-x-1=0}$의 해인 무리수이며, 그 값은 다음과 같다.^[4][5]

${\displaystyle n}$차 버터워스 다항식은 합으로도 쓸 수 있다.

${\displaystyle B_{n}(s)=\sum _{k=0}^{n}a_{k}s^{k}\,,}$

계수 ${\displaystyle a_{k}}$는 재귀 공식^[6][7]으로 다음과 같이 주어진다.

${\displaystyle {\frac {a_{k+1}}{a_{k}}}={\frac {\cos(k\gamma )}{\sin((k+1)\gamma )}}}$

그리고 곱 공식으로 다음과 같이 주어진다.

${\displaystyle a_{k}=\prod _{\mu =1}^{k}{\frac {\cos((\mu -1)\gamma )}{\sin(\mu \gamma )}}\,,}$

여기서

${\displaystyle a_{0}=1\qquad {\text{and}}\qquad \gamma ={\frac {\pi }{2n}}\,.}$

또한, ${\displaystyle a_{k}=a_{n-k}}$이다. 처음 10개의 버터워스 다항식 ${\displaystyle B_{n}(s)}$에 대한 반올림된 계수 ${\displaystyle a_{k}}$는 다음과 같다.

소수점 넷째 자리까지의 버터워스 계수 ${\displaystyle a_{k}}$

${\displaystyle n}$	${\displaystyle a_{0}}$	${\displaystyle a_{1}}$	${\displaystyle a_{2}}$	${\displaystyle a_{3}}$	${\displaystyle a_{4}}$	${\displaystyle a_{5}}$	${\displaystyle a_{6}}$	${\displaystyle a_{7}}$	${\displaystyle a_{8}}$	${\displaystyle a_{9}}$	${\displaystyle a_{10}}$
${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$
${\displaystyle 2}$	${\displaystyle 1}$	${\displaystyle 1.4142}$	${\displaystyle 1}$
${\displaystyle 3}$	${\displaystyle 1}$	${\displaystyle 2}$	${\displaystyle 2}$	${\displaystyle 1}$
${\displaystyle 4}$	${\displaystyle 1}$	${\displaystyle 2.6131}$	${\displaystyle 3.4142}$	${\displaystyle 2.6131}$	${\displaystyle 1}$
${\displaystyle 5}$	${\displaystyle 1}$	${\displaystyle 3.2361}$	${\displaystyle 5.2361}$	${\displaystyle 5.2361}$	${\displaystyle 3.2361}$	${\displaystyle 1}$
${\displaystyle 6}$	${\displaystyle 1}$	${\displaystyle 3.8637}$	${\displaystyle 7.4641}$	${\displaystyle 9.1416}$	${\displaystyle 7.4641}$	${\displaystyle 3.8637}$	${\displaystyle 1}$
${\displaystyle 7}$	${\displaystyle 1}$	${\displaystyle 4.4940}$	${\displaystyle 10.0978}$	${\displaystyle 14.5918}$	${\displaystyle 14.5918}$	${\displaystyle 10.0978}$	${\displaystyle 4.4940}$	${\displaystyle 1}$
${\displaystyle 8}$	${\displaystyle 1}$	${\displaystyle 5.1258}$	${\displaystyle 13.1371}$	${\displaystyle 21.8462}$	${\displaystyle 25.6884}$	${\displaystyle 21.8462}$	${\displaystyle 13.1371}$	${\displaystyle 5.1258}$	${\displaystyle 1}$
${\displaystyle 9}$	${\displaystyle 1}$	${\displaystyle 5.7588}$	${\displaystyle 16.5817}$	${\displaystyle 31.1634}$	${\displaystyle 41.9864}$	${\displaystyle 41.9864}$	${\displaystyle 31.1634}$	${\displaystyle 16.5817}$	${\displaystyle 5.7588}$	${\displaystyle 1}$
${\displaystyle 10}$	${\displaystyle 1}$	${\displaystyle 6.3925}$	${\displaystyle 20.4317}$	${\displaystyle 42.8021}$	${\displaystyle 64.8824}$	${\displaystyle 74.2334}$	${\displaystyle 64.8824}$	${\displaystyle 42.8021}$	${\displaystyle 20.4317}$	${\displaystyle 6.3925}$	${\displaystyle 1}$

정규화된 버터워스 다항식은 임의의 로우패스 필터 차단 주파수 ${\displaystyle \omega _{c}}$에 대한 전달 함수를 결정하는 데 사용할 수 있다.

${\displaystyle H(s)={\frac {G_{0}}{B_{n}(a)}}}$ , 여기서 ${\displaystyle a={\frac {s}{\omega _{c}}}.}$

다른 대역 형태로의 변환도 가능하다. 시제품 필터를 참고하라.

최대 평탄성

${\displaystyle \omega _{c}=1}$ 및 ${\displaystyle G_{0}=1}$이라고 가정하면, 주파수에 대한 이득의 미분은 다음과 같이 나타낼 수 있다.

${\displaystyle {\frac {dG}{d\omega }}=-nG^{3}\omega ^{2n-1}}$

이는 이득 ${\displaystyle G}$가 항상 양수이므로 모든 ${\displaystyle \omega }$에 대해 단조적으로 감소한다. 따라서 버터워스 필터의 이득 함수는 잔물결이 없다. 이득 함수의 급수 전개는 다음과 같다.

${\displaystyle G(\omega )=1-{\frac {1}{2}}\omega ^{2n}+{\frac {3}{8}}\omega ^{4n}+\ldots }$

다른 말로, 2${\displaystyle n}$차 미분을 포함하지 않는 이득의 모든 미분은 ${\displaystyle \omega =0}$에서 0이 되어 "최대 평탄성"을 갖게 된다. 단조성의 요구 사항이 통과 대역에만 국한되고 저지 대역에 잔물결이 허용된다면, "최대 평탄" 버터워스 필터보다 통과 대역에서 더 평탄한 역체비셰프 필터와 같은 동일 차수의 필터를 설계하는 것이 가능하다.

고주파 롤오프

다시 ${\displaystyle \omega _{c}=1}$이라고 가정하면, 큰 ${\displaystyle \omega }$에 대한 이득의 로그 기울기는 다음과 같다.

${\displaystyle \lim _{\omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega )}}=-n.}$

데시벨 단위로, 고주파 롤오프는 따라서 20${\displaystyle n}$ dB/decade 또는 6${\displaystyle n}$ dB/octave이다(20배수는 전력이 전압 이득의 제곱에 비례하기 때문에 사용된다. 20 log rule을 참고하라).

최소 차수

최소 개수의 소자를 사용하여 버터워스 필터를 설계하기 위해, 버터워스 필터의 최소 차수는 다음과 같이 계산할 수 있다.^[8]

${\displaystyle n=\left\lceil {\frac {\log {{\bigr (}{\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}{\bigr )}}{2\log {(\omega _{s}/\omega _{p})}}}\right\rceil }$

여기서:

${\displaystyle \omega _{p}}$ 및 ${\displaystyle \alpha _{p}}$는 통과대역 주파수 및 해당 주파수에서의 감쇠(dB 단위)이다.

${\displaystyle \omega _{s}}$ 및 ${\displaystyle \alpha _{s}}$는 저지대역 주파수 및 해당 주파수에서의 감쇠(dB 단위)이다.

${\displaystyle n}$은 최소 극 개수, 즉 필터의 차수이다.

${\displaystyle \lceil \cdot \rceil }$는 천장 함수를 나타낸다.

비표준 차단 감쇠

버터워스 필터의 차단 감쇠는 일반적으로 -3.01 dB로 정의된다. 차단 주파수에서 다른 감쇠를 사용하고자 한다면, 각 극에 다음 계수를 적용할 수 있으며, 그러면 극은 원 위에 계속 놓이지만 반경은 더 이상 단위가 되지 않는다.^[8] 차단 감쇠 방정식은 페이지 상단에 명시된 버터워스 정의 방정식의 대수 조작을 통해 도출될 수 있다.^[9]

$${\displaystyle {\begin{aligned}p_{A}=p_{1}\times (10^{\alpha /10}-1)^{{-1}/{2n}}&\qquad {\text{For 0}}\leq \alpha <\infty \end{aligned}}}$$

여기서:

${\displaystyle p_{A}}$는 원하는 차단 감쇠를 설정하도록 재배치된 극이다.

${\displaystyle p_{1}}$은 단위 원 위에 놓이는 -3.01 dB 차단 극이다.

${\displaystyle \alpha }$는 차단 주파수에서 원하는 감쇠(dB 단위, 1 dB, 10 dB 등)이다.

${\displaystyle n}$은 극 개수, 즉 필터의 차수이다.

필터 구현 및 설계

선형 아날로그 필터를 구현하기 위해 사용할 수 있는 여러 가지 필터 토폴로지가 있다. 수동 구현에 가장 자주 사용되는 토폴로지는 카우어 토폴로지이고, 능동 구현에 가장 자주 사용되는 토폴로지는 셀렌-키 토폴로지이다.

카우어 토폴로지

카우어 토폴로지를 사용한 버터워스 필터

카우어 토폴로지는 수동 소자(병렬 콘덴서 및 직렬 유도자)를 사용하여 선형 아날로그 필터를 구현한다. 주어진 전달 함수를 갖는 버터워스 필터는 카우어 1형을 사용하여 실현할 수 있다. k번째 소자는 다음으로 주어진다.^[10]

${\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{odd}}}$

${\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{even}}.}$

원한다면 직렬 유도자로 시작할 수 있으며, 이 경우 L_k는 k가 홀수이고 C_k는 k가 짝수이다. 이 공식들은 L_k와 C_k를 모두 g_k와 같게 만들어서 유용하게 결합할 수 있다. 즉, g_k는 이미턴스를 s로 나눈 값이다.

${\displaystyle g_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k=1,2,3,\ldots ,n.}$

이 공식들은 ${\displaystyle \omega }$_c = 1인 양측 종단 필터(즉, 소스 및 부하 온저항이 모두 1과 같음)에 적용된다. 이 시제품 필터는 다른 온저항 및 주파수 값에 대해 스케일링할 수 있다. 단일 종단 필터(즉, 이상적인 전압 또는 전류원에 의해 구동되는 필터)의 경우 소자 값은 다음으로 주어진다.^[3]

${\displaystyle g_{j}={\frac {a_{j}a_{j-1}}{c_{j-1}g_{j-1}}}\qquad j=2,3,\ldots ,n}$

여기서

${\displaystyle g_{1}=a_{1}}$

그리고

${\displaystyle a_{j}=\sin \left[{\frac {(2j-1)}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n}$

${\displaystyle c_{j}=\cos ^{2}\left[{\frac {j}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n.}$

전압 구동 필터는 직렬 소자로 시작해야 하고 전류 구동 필터는 병렬 소자로 시작해야 한다. 이 형식들은 다이플렉서 및 멀티플렉서 설계에 유용하다.^[3]

셀렌-키 토폴로지

셀렌-키 토폴로지

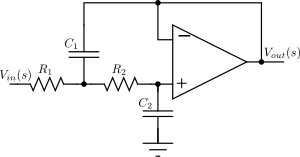
셀렌-키 토폴로지는 능동 및 수동 소자(비반전 버퍼, 일반적으로 연산 증폭기, 저항, 콘덴서)를 사용하여 선형 아날로그 필터를 구현한다. 각 셀렌-키 단은 공액 극 쌍을 구현한다. 전체 필터는 모든 단을 직렬로 캐스케이드하여 구현된다. 실수 극이 있는 경우(${\displaystyle n}$이 홀수인 경우), 이는 별도로, 일반적으로 RC 회로로 구현하고 능동 단과 캐스케이드 해야 한다.

오른쪽에 표시된 2차 셀렌-키 회로에 대한 전달 함수는 다음으로 주어진다.

${\displaystyle H(s)={\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {1}{1+C_{2}(R_{1}+R_{2})s+C_{1}C_{2}R_{1}R_{2}s^{2}}}.}$

분모가 버터워스 다항식의 2차 항 중 하나이기를 바란다. ${\displaystyle \omega _{c}=1}$이라고 가정하면, 이는 다음을 의미한다.

${\displaystyle C_{1}C_{2}R_{1}R_{2}=1\,}$

그리고

${\displaystyle C_{2}(R_{1}+R_{2})=-2\cos \left({\frac {2k+n-1}{2n}}\pi \right).}$

이것은 임의로 선택할 수 있는 두 개의 미정 구성 요소 값을 남겨둔다.

하나의 연산 증폭기만 사용하는 3차 및 4차 셀렌-키 토폴로지를 갖는 버터워스 로우패스 필터는 Huelsman^[11][12]에 의해 기술되었으며, Jurišić 외 연구진에 의해 더 높은 차수의 단일 앰프 버터워스 필터도 제시되었다.^[13]

디지털 구현

버터워스 및 다른 필터의 디지털 구현은 종종 아날로그 필터 설계를 이산화하는 두 가지 다른 방법인 쌍선형 변환 방법 또는 매칭 Z 변환 방법에 기반한다. 버터워스와 같은 전극 필터의 경우, 매칭 Z 변환 방법은 임펄스 불변 방법과 동일하다. 고차의 경우, 디지털 필터는 양자화 오류에 민감하므로 홀수 차수에 대해 종종 캐스케이드된 바이쿼드 섹션과 하나의 1차 또는 3차 섹션으로 계산된다.

다른 선형 필터와의 비교

버터워스 필터의 속성은 다음과 같다.

• 통과대역과 저지대역 모두에서 단조 진폭 응답
• 차단 주파수 주변에서 빠른 롤오프, 이는 차수가 증가함에 따라 향상됨
• 계단 응답에서 상당한 오버슈트 및 링잉, 이는 차수가 증가함에 따라 악화됨
• 약간 비선형적인 위상 응답
• 주파수에 크게 의존하는 군지연

다음은 다른 일반적인 필터 유형과 함께 이산 시간 버터워스 필터의 이득을 보여주는 이미지이다. 이 필터는 모두 5차 필터이다.

버터워스 필터는 체비셰프 필터 또는 타원 필터보다 차단 주파수 주변에서 더 느리게 롤오프하지만, 잔물결이 없다.

같이 보기

• 베셀 필터
• 체비셰프 필터
• 콤 필터
• 타원 필터
• 필터 설계