완전수

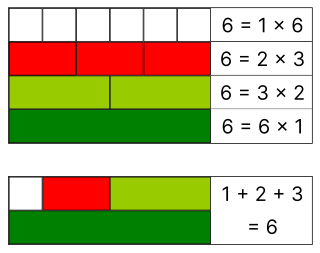
완전수(完全數, 영어: perfect number)는 수론에서 자신을 제외한 양의 약수의 합과 같은 양의 정수를 가리킨다.^[1] 예를 들어, 6의 진약수는 1, 2, 3이며, 1 + 2 + 3 = 6이므로 6은 완전수다. 다음 완전수는 28인데, 1 + 2 + 4 + 7 + 14 = 28이기 때문이다.

완전수 6을 퀴즈네어 막대로 표현한 그림

처음 일곱 개의 완전수는 6, 28, 496, 8128, 33550336, 8589869056, 137438691328이다.^[2]

수의 진약수의 합은 진약수의 합이라 불리며, 따라서 완전수는 진약수의 합과 같은 수다. 이와 같은 말로 완전수는 모든 양의 약수의 합의 절반과 같은 수다. 기호로 표현하면, ${\displaystyle \sigma _{1}(n)=2n}$이며, 여기서 ${\displaystyle \sigma _{1}}$은 약수 함수다.

이 정의는 고대부터 있었으며, 에우클레이데스의 원론 (VII.22)에 τέλειος ἀριθμός(완전, 이상적 또는 완전한 수)로 처음 등장한다. 에우클레이데스는 또한 ${\displaystyle q}$가 양의 정수 ${\displaystyle p}$에 대해 ${\displaystyle 2^{p}-1}$ 형태의 소수일 때, ${\textstyle {\frac {q(q+1)}{2}}}$가 짝수 완전수임을 증명했다(IX.36). 이것은 오늘날 메르센 소수라고 불린다. 2천 년 후, 레온하르트 오일러는 모든 짝수 완전수가 이 형태임을 증명했다.^[3] 이것은 에우클레이데스-오일러 정리로 알려져 있다.

홀수 완전수가 존재하는지, 또는 무한히 많은 완전수가 존재하는지는 알려져 있지 않다.

역사

기원전 약 300년에 에우클레이데스는 2^p − 1이 소수이면 2^p−1(2^p − 1)이 완전수임을 보였다. 처음 네 개의 완전수는 초기 그리스 수학에서 알려진 유일한 수였고, 수학자 니코마코스는 이미 서기 약 100년에 8128을 언급했다.^[4] 현대 언어로, 니코마코스는 모든 완전수가 ${\displaystyle 2^{n}-1}$이 소수일 때 ${\displaystyle 2^{n-1}(2^{n}-1)}$ 형태를 가진다고 증명 없이 진술했다.^[5][6] 그는 n 자체가 소수여야 한다는 것을 모르는 것 같았다. 그는 또한 완전수가 6 또는 8로 번갈아 끝난다고 (잘못) 말했다. (첫 5개의 완전수는 6, 8, 6, 8, 6으로 끝나지만, 여섯 번째도 6으로 끝난다.) 알렉산드리아의 필론은 1세기 저서 "창조에 관하여"에서 완전수를 언급하며, 세상이 6일 만에 창조되었고 달이 28일 주기로 공전하는 것은 6과 28이 완전수이기 때문이라고 주장했다. 필론의 뒤를 이어 오리게네스,^[7] 디디모스는 10,000 미만의 완전수가 4개뿐이라는 관찰을 덧붙였다. (창세기 주해 1. 14–19).^[8] 아우구스티누스는 5세기 초 "신국론"(책 XI, 챕터 30)에서 완전수를 정의하며, 신이 6일 만에 세상을 창조한 것은 6이 가장 작은 완전수이기 때문이라는 주장을 반복했다. 이집트 수학자 이스마일 이븐 팔루스 (1194~1252년)는 다음 세 완전수(33,550,336; 8,589,869,056; 137,438,691,328)를 언급했으며, 현재는 잘못된 것으로 알려진 몇 가지를 더 나열했다.^[9] 다섯 번째 완전수에 대한 유럽의 첫 언급은 1456년에서 1461년 사이에 알려지지 않은 수학자가 쓴 필사본이다.^[10] 1588년, 이탈리아 수학자 피에트로 카탈디는 여섯 번째(8,589,869,056)와 일곱 번째(137,438,691,328) 완전수를 확인했으며, 또한 에우클레이데스의 규칙으로 얻은 모든 완전수가 6 또는 8로 끝남을 증명했다.^[11][12][13]

짝수 완전수

 에우클레이데스-오일러 정리 문서를 참고하십시오.

수학의 미해결 문제 무한히 많은 완전수가 존재할까? (더 많은 수학의 미해결 문제 보기)

에우클레이데스는 ${\displaystyle 2^{p-1}(2^{p}-1)}$가 ${\displaystyle 2^{p}-1}$이 소수일 때마다 짝수 완전수임을 증명했다 (원론, 명제 IX.36).

예를 들어, 처음 네 개의 완전수는 소수 p에 대해 ${\displaystyle 2^{p-1}(2^{p}-1)}$ 공식을 통해 생성된다. $${\displaystyle {\begin{aligned}p=2&:\quad 2^{1}(2^{2}-1)=2\times 3=6\\p=3&:\quad 2^{2}(2^{3}-1)=4\times 7=28\\p=5&:\quad 2^{4}(2^{5}-1)=16\times 31=496\\p=7&:\quad 2^{6}(2^{7}-1)=64\times 127=8128.\end{aligned}}}$$

${\displaystyle 2^{p}-1}$ 형태의 소수는 17세기 수도사 마랭 메르센의 이름을 따서 메르센 소수로 알려져 있으며, 그는 수론과 완전수를 연구했다. ${\displaystyle 2^{p}-1}$이 소수이기 위해서는 p 자체가 소수여야 한다. 그러나 소수 p를 가진 모든 ${\displaystyle 2^{p}-1}$ 형태의 수가 소수인 것은 아니다. 예를 들어, 2¹¹ − 1 = 2047 = 23 × 89는 소수가 아니다.^[a] 사실, 메르센 소수는 매우 희귀하다. 68,874,199까지의 약 4백만 개의 소수 p 중에서 ${\displaystyle 2^{p}-1}$이 소수인 경우는 48개에 불과하다.^[14]

니코마코스는 (증명 없이) "모든" 완전수가 ${\displaystyle 2^{n}-1}$이 소수일 때 ${\displaystyle 2^{n-1}(2^{n}-1)}$ 형태를 가진다고 진술했지만, 서기 1000년경 이븐 알하이삼 (알하젠)은 그 정도로 나아가기를 꺼려하며, 대신 (증명 없이) 이 공식이 모든 짝수 완전수를 산출한다고 선언했다.^[15] 레온하르트 오일러가 18세기에 이르러서야 공식 ${\displaystyle 2^{p-1}(2^{p}-1)}$이 모든 짝수 완전수를 산출함을 증명했다. 따라서 짝수 완전수와 메르센 소수 사이에는 일대일 대응이 존재한다. 각 메르센 소수는 하나의 짝수 완전수를 생성하고, 그 반대도 마찬가지이다. 이 결과는 종종 에우클레이데스-오일러 정리라고 불린다.

GIMPS 분산 컴퓨팅 프로젝트의 철저한 탐색 결과, 처음 49개의 짝수 완전수는 다음과 같은 ${\displaystyle p}$에 대해 ${\displaystyle 2^{p-1}(2^{p}-1)}$ 형태를 갖는 것으로 밝혀졌다.

p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609, 57885161, 74207281  A000043.^[14]

세 개의 더 큰 완전수도 발견되었는데, 이들은 p = 77232917, 82589933, 136279841에 해당한다. 이 범위 내에 다른 수가 존재할 가능성은 여전히 있지만, GIMPS의 초기 철저한 테스트 결과 p가 137750177 미만인 다른 완전수는 발견되지 않았다. 2025년 기준 52개의 메르센 소수가 알려져 있으며,^[16] 따라서 52개의 짝수 완전수가 있다 (이 중 가장 큰 것은 2^136279840 × (2^136279841 − 1)로 82,048,640자리 숫자이다). 무한히 많은 완전수가 존재하는지, 또는 무한히 많은 메르센 소수가 존재하는지는 알려져 있지 않다.

${\displaystyle 2^{p-1}(2^{p}-1)}$ 형태를 가지는 것 외에도, 모든 짝수 완전수는 ${\displaystyle (2^{p}-1)}$번째 삼각수이며 (따라서 1부터 ${\displaystyle 2^{p}-1}$까지의 정수의 합과 같다) ${\displaystyle 2^{p-1}}$번째 육각수이다. 또한 6을 제외한 모든 짝수 완전수는 ${\displaystyle {\tfrac {2^{p}+1}{3}}}$번째 중심있는 구각수이며, 처음 ${\displaystyle 2^{\frac {p-1}{2}}}$개의 홀수 세제곱수의 합과 같다.(즉, ${\displaystyle 2^{\frac {p+1}{2}}-1}$의 세제곱까지의 홀수 세제곱수이다)

$${\displaystyle {\begin{alignedat}{3}6&=2^{1}(2^{2}-1)&&=1+2+3,\\[8pt]28&=2^{2}(2^{3}-1)&&=1+2+3+4+5+6+7\\&&&=1^{3}+3^{3}\\[8pt]496&=2^{4}(2^{5}-1)&&=1+2+3+\cdots +29+30+31\\&&&=1^{3}+3^{3}+5^{3}+7^{3}\\[8pt]8128&=2^{6}(2^{7}-1)&&=1+2+3+\cdots +125+126+127\\&&&=1^{3}+3^{3}+5^{3}+7^{3}+9^{3}+11^{3}+13^{3}+15^{3}\\[8pt]33550336&=2^{12}(2^{13}-1)&&=1+2+3+\cdots +8189+8190+8191\\&&&=1^{3}+3^{3}+5^{3}+\cdots +123^{3}+125^{3}+127^{3}\end{alignedat}}}$$

짝수 완전수(6 제외)는 다음과 같은 형태를 갖는다. $${\displaystyle T_{2^{p}-1}=1+{\frac {(2^{p}-2)\times (2^{p}+1)}{2}}=1+9\times T_{(2^{p}-2)/3}}$$

각각의 결과 삼각수 (완전수에서 1을 뺀 후 결과를 9로 나눈 값)는 3 또는 5로 끝나며, 수열은 T₇ = 28, T₃₁ = 496, T₁₂₇ = 8128로 시작하며, 이어서 T₂ = 3, T₁₀ = 55, T₄₂ = 903, T₂₇₃₀ = 3727815, ...^[17] 따라서 6을 제외한 모든 짝수 완전수의 자릿수를 더하고, 그 결과 숫자의 자릿수를 더하고, 이 과정을 한 자리 숫자(자릿수근)가 나올 때까지 반복하면 항상 숫자 1이 나온다. 예를 들어, 8128의 자릿수근은 1이다. 왜냐하면 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, 그리고 1 + 0 = 1이기 때문이다. 이는 홀수 소수 p를 갖는 모든 완전수 ${\displaystyle 2^{p-1}(2^{p}-1)}$에 적용되며, 사실 홀수 정수 (반드시 소수일 필요는 없는) m에 대해 "모든" ${\displaystyle 2^{m-1}(2^{m}-1)}$ 형태의 수에 적용된다.

${\displaystyle 2^{p-1}(2^{p}-1)}$ 형태 때문에, 모든 짝수 완전수는 이진법으로 p개의 1 뒤에 p − 1개의 0이 붙는 형태로 표현된다. 예를 들어,

$${\displaystyle {\begin{array}{rcl}6_{10}=&2^{2}+2^{1}&=110_{2}\\28_{10}=&2^{4}+2^{3}+2^{2}&=11100_{2}\\496_{10}=&2^{8}+2^{7}+2^{6}+2^{5}+2^{4}&=111110000_{2}\\8128_{10}=&\!\!2^{12}+2^{11}+2^{10}+2^{9}+2^{8}+2^{7}+2^{6}\!\!&=1111111000000_{2}\end{array}}}$$

따라서 모든 짝수 완전수는 유해수이다.

모든 짝수 완전수는 또한 실용수이다. (참고: 관련 개념)

홀수 완전수

수학의 미해결 문제 홀수 완전수가 존재할까? (더 많은 수학의 미해결 문제 보기)

홀수 완전수가 존재하는지는 알려져 있지 않지만, 다양한 결과가 도출되었다. 1496년, 자크 르페브르 데타플은 에우클레이데스의 규칙이 모든 완전수를 제공한다고 진술하여,^[18] 홀수 완전수가 존재하지 않는다는 것을 암시했지만, 오일러 자신은 "홀수 완전수가 존재하는지는... 매우 어려운 질문이다"라고 말했다.^[19] 최근에는 칼 포메란스가 홀수 완전수가 실제로 존재하지 않음을 시사하는 경험적 논증을 제시했다.^[20] 모든 완전수는 또한 조화 약수수이며, 1을 제외하고는 홀수 조화 약수수가 없다는 추측도 제기되었다. 홀수 완전수에 대해 증명된 많은 속성들은 데카르트 수에도 적용되며, 페이스 닐슨은 이 숫자들에 대한 충분한 연구가 홀수 완전수가 존재하지 않는다는 증명으로 이어질 수 있다고 제안했다.^[21]

홀수 완전수 N은 다음 조건을 만족해야 한다.

• N > 10¹⁵⁰⁰.^[22]
• N은 105로 나누어지지 않는다.^[23]
• N은 N ≡ 1 (mod 12) 또는 N ≡ 117 (mod 468) 또는 N ≡ 81 (mod 324)의 형태를 갖는다.^[24]
• N의 가장 큰 소인수는 10⁸보다 크고,^[25] ${\displaystyle {\sqrt[{3}]{3N}}}$보다 작다.^[26]
• 두 번째로 큰 소인수는 10⁴보다 크고,^[27] ${\displaystyle {\sqrt[{5}]{2N}}}$보다 작다.^[28]
• 세 번째로 큰 소인수는 100보다 크고,^[29] ${\displaystyle {\sqrt[{6}]{2N}}}$보다 작다.^[30]
• N은 적어도 101개의 소인수와 적어도 10개의 서로 다른 소인수를 갖는다.^[22][31] 3이 N을 나누지 않으면, N은 적어도 12개의 서로 다른 소인수를 갖는다.^[32]
• N은 다음과 같은 형태를 갖는다.

${\displaystyle N=q^{\alpha }p_{1}^{2e_{1}}\cdots p_{k}^{2e_{k}},}$

여기서:

• q, p₁, ..., p_k는 서로 다른 홀수 소수이다 (오일러).
• q ≡ α ≡ 1 (mod 4)이다 (오일러).
• N의 가장 작은 소인수는 최대 ${\textstyle {\frac {k-1}{2}}}$이다.^[33]
• N을 나누는 소수 거듭제곱 중 적어도 하나는 10⁶²를 초과한다.^[22]
• ${\displaystyle N<2^{(4^{k+1}-2^{k+1})}}$^[34][35]
• ${\textstyle \alpha +2e_{1}+2e_{2}+2e_{3}+\cdots +2e_{k}\geq {\frac {99k-224}{37}}}$.^[33][36][37]
• ${\displaystyle qp_{1}p_{2}p_{3}\cdots p_{k}<2N^{\frac {17}{26}}}$.^[38]
• ${\textstyle {\frac {1}{q}}+{\frac {1}{p_{1}}}+{\frac {1}{p_{2}}}+\cdots +{\frac {1}{p_{k}}}<\ln 2}$.^[39][40]

또한 지수 e₁, ..., e_k에 대해 몇 가지 사소한 결과가 알려져 있다.

• 모든 e_i ≡ 1 (mod 3)은 아니다.^[41]
• 모든 e_i ≡ 2 (mod 5)는 아니다.^[42]
• 모든 e_i ≡ 1 (mod 3) 또는 2 (mod 5)이면, N의 가장 작은 소인수는 10⁸과 10¹⁰⁰⁰ 사이에 있어야 한다.^[42]
• 더 일반적으로, 모든 2e_i+1이 주어진 유한 집합 S에 소인수를 가지면, N의 가장 작은 소인수는 S에만 의존하는 효과적으로 계산 가능한 상수보다 작아야 한다.^[42]
• (e₁, ..., e_k) =  (1, ..., 1, 2, ..., 2)이고 t개의 1과 u개의 2가 있다면, ${\textstyle {\frac {t-1}{4}}\leq u\leq 2t+{\sqrt {\alpha }}}$이다.^[43]
• (e₁, ..., e_k) ≠ (1, ..., 1, 3),^[44] (1, ..., 1, 5), (1, ..., 1, 6).^[45]
• e₁ = ... = e_k = e인 경우,
  • e는 3,^[46] 5, 24,^[47] 6, 8, 11, 14 또는 18일 수 없다.^[45]
  • ${\displaystyle k\leq 2e^{2}+8e+2}$이고 ${\displaystyle N<2^{4^{2e^{2}+8e+3}}}$이다.^[48]

1888년, 제임스 조지프 실베스터는 다음과 같이 말했다.^[49]

... 이 [홀수 완전수]가 존재한다면, 즉, 모든 면에서 자신을 둘러싼 복잡한 조건의 거미줄을 피하는 데 성공한다면 그것은 기적에 가까울 것이다.

반면에, 여러 홀수가 완전수에 가깝다. 르네 데카르트는 D = 3² ⋅ 7² ⋅ 11² ⋅ 13² ⋅ 22021 = (3⋅1001)² ⋅ (22⋅1001 − 1) = 198585576189이 22021 (= 19² ⋅ 61)이 소수였다면 홀수 완전수가 될 것이라고 관찰했다. 이 속성을 가진 홀수 (합성 인수 중 하나가 소수였다면 완전수가 될 수 있는 수)은 데카르트 수이다.

사소한 결론

모든 짝수 완전수는 매우 정확한 형태를 가지며, 홀수 완전수는 존재하지 않거나 희귀하다. 완전수에 대해 증명하기는 매우 쉽지만 겉보기에는 인상적인 결과가 많이 있다. 그 중 일부는 리처드 K. 가이의 작은 수의 강력한 법칙에도 속한다.

• n³ + 1 형태의 유일한 짝수 완전수는 28이다 (Makowski 1962).^[50]
• 28은 또한 두 양의 정수 세제곱의 합인 유일한 짝수 완전수이다 (Gallardo 2010).^[51]
• 완전수 N의 약수들의 역수들의 합은 2가 되어야 한다 (이를 얻기 위해 완전수의 정의 ${\displaystyle \sigma _{1}(n)=2n}$을 양변을 n으로 나눈다).
  • 6의 경우, ${\textstyle {\frac {1}{6}}+{\frac {1}{3}}+{\frac {1}{2}}+{\frac {1}{1}}={\frac {1}{6}}+{\frac {2}{6}}+{\frac {3}{6}}+{\frac {6}{6}}={\frac {1+2+3+6}{6}}={\frac {2\cdot 6}{6}}=2}$이다.
  • 28의 경우, ${\textstyle {\frac {1}{28}}+{\frac {1}{14}}+{\frac {1}{7}}+{\frac {1}{4}}+{\frac {1}{2}}+{\frac {1}{1}}=2}$ 등이다.
• 완전수 (짝수든 홀수든)의 약수의 개수는 짝수여야 한다. 왜냐하면 N은 완전 제곱수가 될 수 없기 때문이다.^[52]
  • 이 두 결과로부터 모든 완전수는 오어의 조화수임을 알 수 있다.
• 짝수 완전수는 사다리꼴 수가 아니다. 즉, 서로 다른 두 개의 연속하지 않는 양의 삼각수의 차이로 표현할 수 없다. 사다리꼴 수가 아닌 숫자는 세 가지 유형만 있다. 짝수 완전수, 2의 거듭제곱, 페르마 소수 ${\displaystyle 2^{n}+1}$과 2의 거듭제곱의 곱으로 이루어진 ${\displaystyle 2^{n-1}(2^{n}+1)}$ 형태의 수로, 메르센 소수에서 짝수 완전수를 구성하는 방식과 유사하다.^[53]
• n 미만의 완전수 개수는 ${\displaystyle c{\sqrt {n}}}$ 미만인데, 여기서 c > 0은 상수이다.^[54] 사실 o(${\displaystyle {\sqrt {n}}}$)이다.^[55]
• 모든 짝수 완전수는 십진법에서 6 또는 28로 끝나며, 6을 제외하고는 구진법에서 1로 끝난다.^[56][57] 따라서 특히 6을 제외한 모든 짝수 완전수의 자릿수근은 1이다.
• 유일한 제곱 인수가 없는 완전수는 6이다.^[58]

관련 개념

100 미만의 수에 대한 오일러 다이어그램

   과잉수

   원시 과잉수

   고도 과잉수

   초과잉수 및 고도 합성수

   거대 과잉수 및 초고도 합성수

   기묘수

   완전수

   합성수

   부족수

진약수의 합은 다양한 다른 종류의 숫자를 제공한다. 합이 그 수 자체보다 작으면 부족수라고 하고, 합이 그 수 자체보다 크면 과잉수라고 한다. 이 용어들은 '완전수' 자체와 함께 그리스 수비학에서 유래했다. 서로의 진약수의 합이 되는 두 수의 쌍은 친화수라고 불리며, 더 큰 수의 주기는 사교수라고 불린다. 모든 작은 양의 정수가 자신과 구별되는 약수들의 합인 양의 정수는 실용수이다.

정의에 따르면, 완전수는 고정점이며, s(n) = σ(n) − n으로 정의되는 약수 함수의 고정점이며, 완전수와 관련된 진약수의 합은 상수 수열이다. 모든 완전수는 또한 ${\displaystyle {\mathcal {S}}}$-완전수, 즉 그랜빌 수이다.

반완전수는 자신 또는 일부 진약수의 합과 같은 자연수이다. 모든 진약수의 합과 같은 반완전수는 완전수이다. 대부분의 과잉수는 또한 반완전수이다. 반완전수가 아닌 과잉수는 기묘수라고 불린다.

같이 보기

• 조화 약수수
• 초완전수
• 렌스터 집합
• 메르센 소수와 완전수 목록
• 배수 완전수
• 초완전수
• 유니타리 완전수

내용주

1. ${\displaystyle 2^{p}-1}$의 모든 약수는 1 mod 2p와 합동이다. 예를 들어, 2¹¹ − 1 = 2047 = 23 × 89이며 여기서 23와 89 모두 22로 나누었을 때 나머지가 1이다. 또한 p가 소피 제르맹 소수, 즉 2p + 1도 모두 소수이며 2p + 1가 mod 8 연산으로 1 또는 7이라면 2p + 1은 ${\displaystyle 2^{p}-1}$의 약수가 된다. 이에 해당하는 수는 p = 11, 23, 83, 131, 179, 191, 239, 251, ...  A002515이다.