Коефициент на асиметрија

Мерките на асиметрија во статистиката се вбројуваат во показателите на обликот на распределбата. Во статистичката анализа се воведени мерки на обликот на распределбата за да се диференцираат распределбите од ист степен на хомогеност. Мерки на обликот на распределба се: коефициент на асиметрија и коефициент на сплеснатост (збирно „наклон, накосеност“).

Споредба на средина, медијана и модус на два логаритамски нормални распределби со различна асиметрија (наклон).

Распределбата е асиметрична доколку опсервациите не се симетрично распределени на двете страни.

Мерките на асиметрија се бројчена одлика на начинот на распределбата на податоците. Со помош на мерките на асиметрија се мери начинот на распределба на единиците на статистичката маса спрема некои вредности, односно спрема оската на симетрија. Мерките на обликот на распределбата се пресметуваат со помошни и централни моменти на распределба.^[1]

Пресметување на коефициентот на асиметрија

Коефициентот на асиметрија е релативна мерка на асиметрија. За мерење на асиметријата потребни се отстапувањата на вредностите на бројчената променлива од аритметичката средина – трет централен момент.

• за негрупирани податоци:

${\displaystyle \mu _{3}={\frac {\sum \limits _{i=1}^{N}(x_{i}-{\bar {x}})^{3}}{N}}}$

• за групирани податоци

${\displaystyle \mu _{3}={\frac {\sum \limits _{i=1}^{k}f_{i}(x_{i}-{\bar {x}})^{3}}{N}}}$

Коефициентот на асиметрија (α3) е бројчен показател кој покажува до кој степен определена распределба е симетрична во однос на нормалната. Тој се добива кога третиот централен момент се става во однос со стандардното отстапување на трет степен.

формула за коефициент на асиметрија:

${\displaystyle \alpha _{3}={\frac {\mu _{3}}{\sigma ^{3}}}}$

Најчесто се движи во интервал [-2, +2] а понекогаш зазема и поголеми вредности.

Коефициентот на асиметрија ги користи сите отстапувања на вредностите на бројчената променлива од аритметичката средина и според тоа таа е потполна мерка на асиметрија.

Кај симетричните распределби на честотите α3 = 0. Ако α3 > 0, тогаш распределбата е позитивно асиметричен (асиметричен на десно). И обратно, ако α3 < 0, тогаш распределбата е негативно асиметрична (асиметрична на лево).
^[2]

Симетрична распределба

позитивно асиметрична распределба

негативно асиметрична распределба

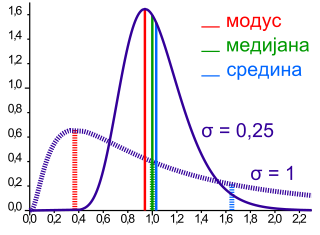
За определување на насоката на асиметријата се користи знакот на третиот централен момент или редот на големините на средните вредности. Кај симетричните распределби важи: М=Ме=Мо. Кај лево асиметричните (негативно асиметричните) важи: М<Ме<Мо. Кај десно асиметричните ( позитивно асиметричните) важи: М>Ме>Мо. Квалитативните толкувања на искривеноста се комплицирани. За едномодална распределба, негативната искривеност укажува на тоа дека опашката на левата страна на густината на веројатност е подолга и подебела од десната страна. Спротивно на тоа, позитивната искривеност укажува на тоа дека опшката од десната страна е подолга и подебела од левата страна. Во случаите каде една опашка е подолга, а другата е подебела, искривеноста не се придржува на едноставното правило. На пример, нула вредност укажува на тоа дека опашките се наоѓаат рамнотежно на двете страни од средината, што е случај кај симетричната распределба, и за асиметричните распределби каде асиметриите се надоместуваат, како на пример, една опашка е долга, но тенка, а другата е кратка и дебела. Понатаму, во повеќемодалните распределби и дисктретни распределби, искривеноста е исто така тешко да се протолкува. Поважно, искривеноста не го утврдува односот на средината и медијаната.

Нормалната распределба е распределба на податоците во облик на ѕвоно, каде средината, медијаната и модата се софпаѓаат. А кривата на честота покажува нормална распределба. Кај нормалната распределба, околу 68% од вредностите лежат во една стандардно отстапување од средината и околу 95% од податоците лежат во две стандардни отстапувања од средината.

Ако има крајните (екстремни) вредности кон позитивниот крај на распределбата, се вели дека распределбата е позитивно искривена. Во позитивно искривената распределба, средината е поголема од модата. Негативна искривеност, од другата страна, има средина која е помала од модата поради присуството на краните вредности на негативниот крај на распределбата.^[3]

Јачина на асиметрија

Во зависност од големината на коефициентот на асиметрија се одредува и јачината на асиметрија.

| α3 | ≤ 0,25 – мала јачина

0,25 < | α3 | ≤ 0,50 – средна јачина

| α3 | > 0,50 – јака јачина^[4]

Доколку коефициентот е во интервал [-0,5; +0,5] тогаш се смета дека распределбата има умерена асиметрија.

Поедноставено пресметување на третиот централен момент

Пресметувањето на третиот централен момент може да се поедностави со формулата:

формула за трет централен момент

Во претходниот израз mr претставува помошен момент дефиниран за:

• за негрупирани податоци

формула за мр од негрупирани податоци

• за групирани податоци

формула за мр од групирани податоци

Користејќи ги помошните моменти може да се пресмета и стандардното отстапување.^[5]

формула за стандардно отстапување

Прв Пирсонов коефициент (β1)

Меѓусебните односи на средните големини и нивните својства, се значајни за изработка на Пирсоновиот модел на коефициентот на асиметрија. Најпогодни за матеметичка анализа се структурните серии со бројчени белези или распределби на честоти. Врз нив се врши комплексна статистичка анализа. Во показателите на распределбите, покрај средните големини и мерките на дисперзија се вбројуваат и мерките на асиметрија и сплеснатост на распределбата кои се однесуваат на неговиот облик.^[6]

Пирсоновата мерка на асиметрија се темели на односите на аритметичката средина и модата,односно медијаната во бројчената низа.

• симетрична распределба
• позитивно асиметрична
• негативно асиметрична

Помеѓу крајот на 19 век и почетокот на 20 век , Карл Пирсон истражувал огромни бази на податоци од кои некои значително се разликувале од нормалните распределби и воедно ги изучувал таквите отстапувања. За таа цел го конструирал коефициентот на асиметрија, кој според него е наречен прв Пирсонов коефициент. Според оваа мерка доколку коефициентот е еднаков на нула распределбите се симетрични. Тој открил дека за умерено асиметричната распределба каде што Мо е ознака за модус и Ме ознака за медијана: Мо - ẍ≈ 3*(Ме - ẍ )^[7]

Пирсоновиот коефициент претставува однос на разликата на аритметичката средина и модусот спрема стандардното отстапување.

формула за пирсонов коефициент

Пирсоновите мерки се дадени со изразот:

Пирсоновиот коефициент вообичаено се движи во интервал [-3; +3].

Доколку распределбата Sk=0 има симетричен облик. Ако Sk = ±3 се смета дека распределбата има позитивна или негативна асиметрија.^[1]

Боулиева мерка на асиметрија

Боулиевата мерка на асиметрија се темели на односите на квартилите и медијаната. Пресметувањето на Боулиевиот коефициент на асиметрија е дадено со изразот:

формула за боулиев коефициент

Вообичаено се движи во интервал ± 1.

Во симетричната распределба, Буловиот коефициент е 0. Во позитивна асиметрија е позитивен, а во негативна асиметрија е негативен.

• симетрична распределба
• позитивна асиметрија
• негативна асиметрија

Буловата и Пирсоновата мерка се непотполни мерки на асиметрија и се помалку информативни од коефициентот на асиметрија, но се пресметуваат поедноставно и побрзо.^[8]

Поврзано

• Симетрија
• Веројатносна распределба