Просек

Во математиката, просек или средна тенденција ^[1] на податоци ја претставува „средната“ или „очекувана“ вредност на податокот. Има различни дескриптивни статистики кои може да се одберат за одредување на средната тенденција на податоците.

Просечната е поединечна вредност која се одликува со различни вредности. Ако сите броеви на списокот се исти, тогаш тој број се применува. А, ако сите броеви не се исти, тогаш најлесен начин да се дојде до претставителна вредност од списокот е случајно да се избере еден број од списокот. И покрај тоа, поимот „просек“ обично се придржува до пософистицирани методи, кои се сметаат за покорисни.

Највообичаениот метод е аритметичката средина. Има многу други видови на просек, како медијана (скоро секогаш се употребува за да се опишат цените и приходите).^[2] Пресекот се пресметува со комбинација на величините поврзани со множеството и за да се пресмета бројот кој е просек во тоа множество.

Пресметка

Споредба на модус, медијана и средина

Аритметичка средина

Главна статија: Аритметичка средина

Ако се дадени ${\displaystyle n}$ броеви, секој број обележан како a_i, каде ${\displaystyle i=1,\dots ,n}$, аритметичката средина е збир од a_i'-те поделен со ${\displaystyle n}$ или

${\displaystyle AM={\frac {1}{n}}\sum _{i=1}^{n}a_{i}}$.

Аритметичката средина, често поедноставно се нарекува средина, ако два броја како 2 и 8 се дадени со претставување на вредноста 2 + 8 = A + A. Вредноста на А е (2 + 8)/2 = 5. Промената на редот 2 и 8 во 8 и 2 не ја менува вредноста добиена за А. Средината 5 не е помала од минимумот 2, и не е поголема од максимумот 8. Ако го зголемиме бројот на елементи на списокот и сакаме да најдеме средна вредност, на пр. аритметичка средина од 2, 8 и 11 се наоѓа со решавање на равенката 2 + 8 + 11 = A + A + A. Каде A = (2 + 8 + 11)/3 = 7.

Повторно, промената на местата на трите елементи во списокот не предизвикува промени во резултатот: A = (8 + 11 + 2)/3 = 7 и дека 7 е меѓу 2 и 11. Овој метод на собирање лесно се применува и важи за списоци и со повеќе елементи. И покрај тоа, средната вредност на списокот од цели броеви не е секогаш цел број. „Просечното семејство има 1,7 деца„ води кон тоа да се заклучи дека „просечниот број на деца во семејството е 1,7“.

Геометриска средина

Главна статија: Геометриска средина

Геометриската средина од n броеви се добива со нивно множење и потоа наоѓање на n-ти корен. Со алгебарски термини, геометриската средина од ${\displaystyle a_{1},a_{2},...,a_{n}}$ е дефинирана како

${\displaystyle GM={\sqrt[{n}]{\prod _{i=1}^{n}a_{i}}}={\sqrt[{n}]{a_{1}a_{2}...a_{n}}}}$

Геометриската средина може да се смета како антилогаритам на аритметичката средина на логаритмите на броевите.

На пр. геометрсика средина од 2 и 8 е ${\displaystyle GM={\sqrt {2\cdot 8}}=4}$.

Хармониска средина

Главна статија: Хармониска средина

Хармониската средина на множеството броеви ${\displaystyle a_{1},a_{2},...,a_{n}}$ се дефинира како реципрочна вредност на аритметичката средина на вредностите на ${\displaystyle a_{i}}$:

${\displaystyle HM={\frac {1}{{\frac {1}{n}}\sum _{i=0}^{n}{\frac {1}{a_{i}}}}}={\frac {n}{{\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+...+{\frac {1}{a_{n}}}}}}$

На пример, ако брзината со која од точката A се стигнува до точката B била 60 км/ч и брзината со која се враќа од точката B до точката A била 40 км/ч, тогаш просечната брзина изнесува ${\displaystyle {\frac {2}{1/60+1/40}}=48}$.

Нееднаквост на AM, GM и HM

Нееднаквоста која ги опфаќа аритметичката, геометриската и хармониската средина за кое било множество на позитивни броеви е:

${\displaystyle AM\geq GM\geq HM}$

Лесно е да се запамети дека ништо не значат буквите A, G и H во нееднаквоста, ако не се знае што означуваат. Видете нееднаквост на аритметичката и геометриската средина.

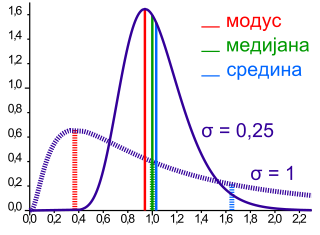
Медијана и модус

Главна статија: Медијана

Медијана е средниот број од група на броеви, кои се распоредени редоследно. (ако има парен број на броеви, тогаш за медијана се аритметичката средина од двата средни броја.)

За да се најде медијаната, потребно е да е најде бројот на елементите, и тогаш да се отстранува по еден број од лево и од десно наизменично, сѐ додека не се дојде до последниот број од лево. Ако остане еден број од лево, тогаш неговата вредност е медијана, а ако останат два тогаш медијаната претставува аритметичка средина на овие два броја. Овој метод во списокот на броеви 1, 7, 3, 13 може да се прочита и како 1, 3, 7, 13. Тогаш 1 и 13 се отстрануваат, по што остануваат само 3 и 7. Бидејќи остануваат само два елементи во списокот, медијаната е нивната аритметичка средина (3 + 7)/2 = 5.

Главна статија: Модус (статистика)

Бројот којшто најмногу пати се појавува во списокот на броеви се нарекува модус. Модусот во списокот на броеви 1, 2, 2, 3, 3, 3, 4 е бројот 3. Модусот не е секогаш дефиниран, така што да има една вредност. Списокот на броеви 1, 2, 2, 3, 3, 5 има два модуси: 2 и 3. Модусот може да се вклучи во главниот метод на дефинирање на просекот со земање на списокот и преместување на секој член, зависно од неговата вредност, почнувајќи од најмалиот. Тогаш, овој списокот е изедначен со дадениот, само што неговите членови се распоредени, почнувајќи од најмалиот. Сега, кога тие се еднакви, тогаш е очигледно да се забележи честота на секој број и да се утврди модусот. Модусот може да се употребува и ако има многу членови во списокот и ако честотата на броевите праволиниски се зголемува (на пр. ако во група од 1.000 луѓе, 30 се со маса 61 кг, 32 тежат 62 кг, 29 тежат 63 кг и ако останатите луѓе се со помала честота за некоја маса, тогаш 62 кг е модус).

Годишно враќање

Годишното враќање е вид на просек кој се користи во финансиите. Тоа е пример на геометриска средина. На пример, ако е даден период од две години и враќањето на вложувањето во првата година изнесува −10%, а во втората +60%, тогаш годишното враќање R, може да се пресмета со решавање на равенката: (1 − 10%) × (1 + 60%) = (1 − 0,1) × (1 + 0,6) = (1 + R) × (1 + R). Вредноста на R за која равенството е точно е 0,2 или 20%. Забележително е дека промената на редоследот во наоѓањето на годишното враќање ма +60% и −10% го дава истиот резултат како и при множењето на враќањата од −10% и +60%.

Овој метод може да се воопшти во примерите во кои сите периоди не се со траење од една година. Годишното враќање е варијација од геометриска средина, која обезбедува интензивна примена на годишното враќање, во согласност со списокот на враќања. На пример, за период од половина година за која враќањето е −23% и период за две и пол години, за кои враќањето е +13%. Годишното враќање за комбинираниот период е единично годишно враќање, R, кое е решение на следнава равенка: (1 − 0,23)^0,5 × (1 + 0,13)^2,5 = (1 + R)^0,5+2,5, што дава вредност на годишното враќање R еднаква на 0,0600 или 6,00%.

Видови

Таблицата на математички симболи ги објаснува симболите користени подолу.

Назив	Равенка или објаснување
Аритметичка средина	${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n})}$
Медијана	Средната вредност, која ги одвојува едната од другата половина од дадените податоци
Геометриска медијана	Вртежна инваријанта проширена од медијаната за вредностите во Rn
Модус	Вредноста која најчесто се појавува во групата на податоци
Геометриска средина	${\displaystyle {\bigg (}\prod _{i=1}^{n}x_{i}{\bigg )}^{1/n}={\sqrt[{n}]{x_{1}\cdot x_{2}\dotsb x_{n}}}}$
Хармониска средина	${\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}}$
Квадратна средина	${\displaystyle {\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{2}}}={\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}{n}}}}$
Експоненцијална средина	${\displaystyle {\sqrt[{p}]{{\frac {1}{n}}\cdot \sum _{i=1}^{n}x_{i}^{p}}}}$
Аритметичка средина на популација	${\displaystyle {\frac {\sum _{i=1}^{n}w_{i}x_{i}}{\sum _{i=1}^{n}w_{i}}}={\frac {w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}}{w_{1}+w_{2}+\cdots +w_{n}}}}$
Скратена средина	Аритметичка средина на вредностите на податоци, по отстранување на најголемиот и најмалиот член од групата
Интерквартална средина	Специјален случај на скратена средина со примена на интерквартален опсег
Среден опсег	${\displaystyle {\frac {\max x+\min x}{2}}}$
Изедначувачка средина	Слично како кај скратената средина, само што не доаѓа до отстранување на екстремните вредности, туку изедначување со најголемата и најмалата вредност којашто остануваат
Годишно враќање	${\displaystyle {\left[\prod (1+R_{i})^{t_{i}}\right]}^{1/\sum t_{i}}-1}$

Решенија на варијациските проблеми

Некои пресметувања на средната тенденција може да се одликуваат како решавање на варијациски проблем, познати и како анализа на варијации, имено минимизациска варијација од средината. Тоа е дадената вредност на статистичка дисперзија, која ја мери средната тенденција на минимизираната варијација: како варијацијата од средината која е еднаква на сите минимуми меѓу сите избори за средината. Духовито речено, „дисперзијата ѝ претходи на локацијата“. Во значењето на ${\displaystyle L^{p}}$ просторот, односите се:

${\displaystyle L^{p}}$	дисперзија	централна тенденција
${\displaystyle L^{1}}$	просечно апсолутно отстапување	медијана
${\displaystyle L^{2}}$	стандардно отстапување	средина
${\displaystyle L^{\infty }}$	максимално отстапување	среден опсег

Стандардното отстапување за средината е помало од стандардното отстапување за некоја друга точка; единственоста на оваа одлика на средината и средниот опсег следува од конвексната оптимизација, како што ${\displaystyle L^{2}}$ и ${\displaystyle L^{\infty }}$ се конвексни функции. Се забележува дека медијаната овде е главен уникат и всушност секоја точка меѓу две средни точки на дискретната распределба го минимизира просечното апсолутно отстапување.

Слично, модусот ја минимизира квалитативната варијација.^{[се бара извор]}

Мешовити видови

Други пософистицирани просеци се: трисредина, тримедијана и нормализираната средина. Овие обично се порепрезентативни до целата група на податоци. ^{[се бара извор]}

Еден може да создаде сопствен просек со примена на Колмогоровата средина:

${\displaystyle y=f^{-1}\left({\frac {f(x_{1})+f(x_{2})+\cdots +f(x_{n})}{n}}\right),}$

каде f е секоја инверзна функција. Хармоничната средина е пример на употребата наf(x) = 1/x и геометриската средина е друга, со примена на f(x) = log x. Друг пример, експоненцијалната средина е средина со примена на функцијата f(x) = e^x и во самата природа се склони вредностите кон најголемата. И покрај тоа, овој метод на експоненцијална средина не е доволен за да се одредат сите средини. Подобар метод за одредување на средината, y, земајќи некоја функција од списокот g(x₁, x₂, ..., x_n), која е симетрична со пермутацијата од членовите во списокот и се изедначува со истата функција со вредност на просечната, распоредувајќи го секој член од списокот: g(x₁, x₂, ..., x_n) = g(y, y, ..., y). Оваа најважна дефиниција има значајна примена во одредувањето на сите просеци од елементите во списокот: Функцијата g(x₁, x₂, ..., x_n) =x₁+x₂+ ...+ x_n ја дава аритметичката средина. Функцијата g(x₁, x₂, ..., x_n) =x₁·x₂· ...· x_n ја дава геометриската средина. Функцијата g(x₁, x₂, ..., x_n) =x₁⁻¹+x₂⁻¹+ ...+ x_n⁻¹ ја дава хармоничната средина ^[3]

Во базата на податоци

Концептот на просечната вредност може да биде претставен како база на податоци, односно голема низа, во рамките на која целта е да се најде вредноста која е на некој начин подеднакво поврзана со секој податок. Базата може да биде распоредена во време, како и збогатениот систем на податоци од којшто се сака да се отстрани збиеноста или просторот, а како во пиксели на сликата од која се сака да се извлече примена. Лесно разбирлива и применувана примена на просечната вредност до базата е едноставниот движечки просек во кој се пресметува аритметичка средина од најсвежите N податоци во базата. За да се напредува една позиција во базата, се додава 1/N пати новиот податок и се одзема 1/N податокот N вратен во базата.

Потекло на поимот

Оригиналното значење на зборот просек е „долготрајна опасност на море“: истиот збор е пронајден во арапскиот јазик како awar, во италијанскиот avaria и во францускиот avarie. Според тоа пресметувач на просек е лице коешто проценува загуба којашто може да се осигура.

Поморскиот ризик е или делумен просек, кој настанува само за сопственикот на ризичниот имот, или хаварија, кога сопственикот може да потврди пропорционални придонеси од сите учесници во поморскиот ризик. Видот на пресметката користена во пресметувањето на хаваријата го зголемува толкувањето на терминот „просек“ како „аритметичка средина“.

Поврзано

• Статистика