Goniometrie

Goniometrie, trigonometrie (Oudgrieks: τρεῖς (treis), drie, γωνία (gōnia), hoek en μετρεῖν (metrein), meten) of driehoeksmeetkunde is een tak van de wiskunde die zich bezighoudt met driehoeken en in het bijzonder de oorspronkelijk op driehoeken gebaseerde goniometrische functies zoals sinus (sin), cosinus (cos) en tangens (tan). Dit is een basisvak van de vlakke meetkunde, omdat alle andere vormen die door rechte lijnen worden ingesloten, opgebouwd kunnen worden uit driehoeken.

Goniometrische cirkel met de desbetreffende aanduiding van de sinus en cosinus van een hoek α.

Sinus en cosinus op de goniometrische cirkel.

De goniometrische cirkel.

De goniometrie kent vele toepassingen, onder andere bij de driehoeksmeting.

De goniometrische cirkel

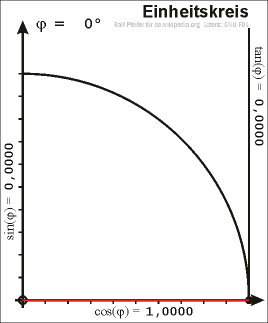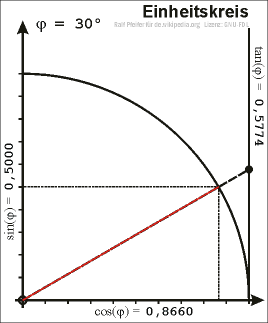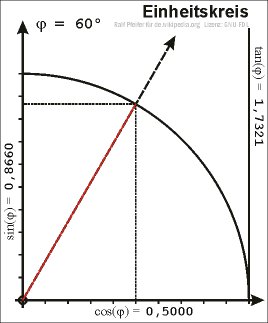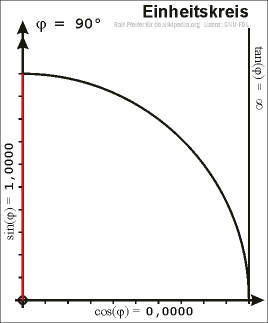
Een goniometrische cirkel of eenheidscirkel is een cirkel met als middelpunt de oorsprong van het assenstelsel en een straal met lengte 1. De voerstraal naar een punt P op de cirkel maakt een hoek ${\displaystyle \alpha }$ met de ${\displaystyle x}$-as. De sinus van deze hoek, ${\displaystyle \sin(\alpha )}$, is gelijk aan de ${\displaystyle y}$-coördinaat van het punt P. De cosinus van de hoek, ${\displaystyle \cos(\alpha )}$, is gelijk aan de ${\displaystyle x}$-coördinaat van het punt P. Hieruit volgt dat de cosinus van ${\displaystyle \alpha }$ gelijk is aan de sinus van het complement van ${\displaystyle \alpha }$, wat de naam cosinus ("complementaire sinus" of "complementsinus") verklaart.

Als punt P de cirkel doorloopt zullen de waarden van ${\displaystyle \cos(\alpha )}$ en ${\displaystyle \sin(\alpha )}$ de waarden doorlopen uit het interval [−1,1].

Ook andere goniometrische getallen krijgen een meetkundige betekenis op de eenheidscirkel. De tangens, gewoonlijk rekenkundig gedefinieerd als het quotiënt van sinus en cosinus, is onder meer ook gelijk aan de ${\displaystyle y}$-coördinaat van het snijpunt van de voerstraal met de rechter verticale raaklijn aan de cirkel (${\displaystyle x=1}$). De cotangens is gelijk aan het omgekeerde van de tangens, maar is ook de ${\displaystyle x}$-coördinaat van het snijpunt van de voerstraal met de bovenste horizontale raaklijn aan de cirkel (${\displaystyle y=1}$). Gelijkaardige constructies leveren de secans (de reciproke van de cosinus) en de cosecans (de reciproke van de sinus).

Met behulp van de goniometrische cirkel kan de hoekeenheid radiaal afgeleid worden: 1 (één) radiaal is de hoek waarbij de booglengte gelijk is aan de straal (${\displaystyle =180^{\circ }\!/\pi }$, is gelijk aan ruim 57°). De booglengte tussen twee punten op de goniometrische cirkel is de absolute waarde van de hoek, uitgedrukt in radialen, tussen de voerstralen naar deze punten.

Tegenwijzerzin is de positieve oriëntatiezin op een goniometrische cirkel. Een hoek gemeten in tegenwijzerzin vanaf het beginbeen tot eindbeen heeft dan een positieve waarde. Meet men in wijzerzin dan heeft de hoek een negatieve waarde.

Geschiedenis

Griekse wetenschappers raakten voor het eerst geïnteresseerd in goniometrische getallen vanuit de praktische noodzaak van sterrenkundige berekeningen. Het belangrijkste Griekse leerboek over astronomie waar we vandaag nog over beschikken, is dat van Ptolemaeus, het best bekend onder de titel van de Arabische vertaling Almagest. Bij Ptolemaeus is de schijnbare beweging van een hemellichaam het resultaat van de samenstelling van de dagelijkse rotatie van de hemelkoepel en de jaarlijkse omwenteling van de zon rond de aarde. Om die samenstelling uit te rekenen heeft hij de lengte van de koorde van een hoek nodig; in moderne terminologie is dat het dubbel van de sinus van de halve hoek, vermenigvuldigd met de straal van de cirkel die bij Ptolemaeus gestandaardiseerd wordt op 60 naar Babylonisch voorbeeld.^[1]

Ook in de Chinese traditie, vastgelegd in het boek Zhoubi Suanjing, ligt de sterrenkunde aan de basis van de goniometrie.^[2]

Relaties tussen hoeken

Met behulp van de cirkel worden de volgende relaties zichtbaar:

${\displaystyle \sin(-\alpha )=-\sin \alpha }$

${\displaystyle \cos(-\alpha )=\cos \alpha }$

${\displaystyle \cos(\alpha )=\sin \left({\frac {\pi }{2}}-\alpha \right)}$

De tangens van een hoek is gedefinieerd als de verhouding tussen ${\displaystyle \sin \alpha }$ en ${\displaystyle \cos \alpha }$, dus:

${\displaystyle \tan \alpha ={\frac {\sin \alpha }{\cos \alpha }}}$

zodat:

${\displaystyle \tan(-\alpha )=-\tan \alpha }$

Uit de stelling van Pythagoras volgt^[3] de grondformule van de goniometrie:

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$

Cotangens (cot), secans (sec) en cosecans (csc) zijn de reciproque functies van respectievelijk: de tangens, cosinus en de sinus.

${\displaystyle \cot \alpha ={\frac {1}{\tan \alpha }}}$

${\displaystyle \sec \alpha ={\frac {1}{\cos \alpha }}}$

${\displaystyle \csc \alpha ={\frac {1}{\sin \alpha }}}$

Met de basisrelaties kan steeds een van de functies in een andere worden uitgedrukt, zij het slechts voor een rechthoekige driehoek. De 'kunst' bij goniometrie is dan ook vaak om een willekeurige driehoek of veelhoek op te delen in rechthoekige driehoeken, zodat de basisrelaties toegepast kunnen worden. De volgende 6 formules gelden voor ${\displaystyle \alpha }$ tussen 0 en ${\displaystyle \pi /2}$ radialen.

${\displaystyle \sin \alpha ={\sqrt {1-\cos ^{2}\alpha }}}$

${\displaystyle \sin \alpha ={\frac {\tan \alpha }{\sqrt {1+\tan ^{2}\alpha }}}}$

${\displaystyle \cos \alpha ={\sqrt {1-\sin ^{2}\alpha }}}$

${\displaystyle \cos \alpha ={\frac {1}{\sqrt {1+\tan ^{2}\alpha }}}}$

${\displaystyle \tan \alpha ={\frac {\sqrt {1-\cos ^{2}\alpha }}{\cos \alpha }}}$

${\displaystyle \tan \alpha ={\frac {\sin \alpha }{\sqrt {1-\sin ^{2}\alpha }}}}$

Verdere omrekenregels

Illustratie van de somregel.

Zie ook

• Nasir al-Din al-Toesi
• Sinus en cosinus
• Tangens en cotangens
• Lijst van goniometrische gelijkheden
• Driehoeksmeting
• Boldriehoeksmeting

Bronnen, noten en/of referenties

1. Hoofdstuk 3 in Hodgkin, Luke, "A History of Mathematics - From Mesopotamia to Modernity," Oxford University Press 2005.
2. Hoofdstuk 4 in Hodgkin, op. cit.
3. Lange tijd werd gedacht dat de Stelling van Pythagoras nodig was voor deze identiteit. Dit is echter niet het geval, zie:
   Jason Zimba (2009) "On the possibility of trigonometric proofs of the Pythagorean theorem" Forum Geometricorum jg. 9, pp. 275-278. Gearchiveerd op 15 april 2023.

Wiskunde

algebra · lineaire algebra · meetkunde · goniometrie · rekenkunde · integraalrekening · getaltheorie · speltheorie · groepentheorie · verzamelingenleer · statistiek · kansrekening · topologie