Top Qs
Linha do tempo
Chat
Contexto
Matemática
ciência que estuda as propriedades e as relações entre os números Da Wikipédia, a enciclopédia livre
Remove ads
Matemática é uma área do conhecimento que inclui os tópicos dos números, fórmulas e estruturas relacionadas, formas e os espaços em que estão contidos, e quantidades e suas mudanças. Esses tópicos são representados na matemática moderna com as principais subdisciplinas da teoria dos números,[1] álgebra,[2] geometria[1] e análise,[3] respectivamente. No entanto, não há consenso entre os matemáticos sobre uma definição comum para a disciplina acadêmica que estudam.
Grande parte da atividade matemática envolve a descoberta de propriedades de objetos abstratos e o uso da razão pura para prová-las. Estes objetos consistem em abstrações da natureza ou — segundo a matemática moderna — entidades que são estipuladas por certas propriedades, chamadas axiomas. Uma prova matemática consiste em uma sucessão de aplicações de regras dedutivas a resultados já estabelecidos. Estes resultados incluem teoremas previamente provados, axiomas e — no caso de abstração da natureza — algumas propriedades básicas que são consideradas pontos de partida da teoria em consideração.[4]
A matemática é essencial nas ciências naturais, engenharia, medicina, finanças, ciências da computação e ciências sociais. Embora seja amplamente utilizada para modelar fenômenos, as verdades fundamentais da matemática são independentes de qualquer experimentação científica. Algumas áreas da matemática, como estatística e teoria dos jogos, são desenvolvidas em estreita correlação com suas aplicações e, portanto, são frequentemente agrupadas na matemática aplicada. Outros campos de estudo são desenvolvidos independentemente de qualquer aplicação (e por este motivo são chamados de matemática pura), mas muitas vezes encontram aplicações práticas posteriormente.[5][6]
Historicamente, o conceito de prova e o rigor matemático associado apareceram pela primeira vez na matemática grega, mais notavelmente na obra Os Elementos de Euclides.[7] Desde o seu início, a matemática foi dividida principalmente em geometria e aritmética (a manipulação de números naturais e frações), até os séculos XVI e XVII, quando a álgebra[a] e o cálculo infinitesimal foram introduzidos como novos campos. Desde então, a interação entre inovações matemáticas e descobertas científicas levou a um aumento correlacionado no desenvolvimento de ambas.[8] No final do século XIX, a crise fundamental da matemática levou à sistematização do método axiomático,[9] que anunciou um aumento dramático no número de áreas matemáticas e seus campos de aplicação.
Remove ads
Etimologia
Resumir
Perspectiva
A palavra matemática vem do grego antigo máthēma e significa "aquilo que se aprende",[10] "aquilo que se conhece", assim como "estudo" e "ciência". A palavra passou a ter o significado mais restrito e técnico de "estudo matemático" mesmo no período clássico.[b] Seu adjetivo é mathēmatikós (μαθηματικός), que significa "relacionado à aprendizagem" ou "estudioso", que também passou a significar "matemático".[14] Em particular, mathēmatikḗ tékhnē (μαθηματικὴ τέχνη; em latim: ars mathematica) significava "a arte matemática".[10]
Da mesma maneira, uma das duas principais escolas de pensamento do pitagorismo era conhecida em grego antigo como mathēmatikoi (μαθηματικοί) — que na época significava "alunos" ao invés do significado moderno dado ao termo "matemáticos". Os pitagóricos foram provavelmente os primeiros a restringir o uso da palavra apenas ao estudo da aritmética e da geometria. Na época de Aristóteles (384-322 a.C.) este significado foi totalmente estabelecido.[15]
Em latim até cerca de 1700, o termo matemática tinha como significado mais comum "astrologia" (ou às vezes "astronomia"); isto mudou gradualmente para o significado atual entre 1500 e 1800. Esta mudança resultou em vários erros de tradução: Por exemplo, a advertência de Santo Agostinho de que os cristãos deveriam tomar cuidado com os mathematici, que significa "astrólogos", às vezes é mal traduzida como uma condenação dos matemáticos.[16]
Remove ads
Áreas da matemática
Resumir
Perspectiva
Antes do período do Renascimento, a matemática era dividida em duas áreas principais: a aritmética, a manipulação dos números, e a geometria, o estudo das formas.[17] Alguns tipos de pseudociência, como a numerologia e a astrologia, não eram então claramente distinguidas da matemática.[18]
Durante o período do Renascimento, surgiram mais dois campos de estudo matemáticos. A notação deu origem à álgebra que, a grosso modo, consiste no estudo e na manipulação de fórmulas. O cálculo, que consiste nos dois subcampos diferencial e integral, é o estudo de funções contínuas que modelam as relações tipicamente não lineares entre quantidades representadas por variáveis. Esta divisão em quatro áreas principais – aritmética, geometria, álgebra, cálculo[19] – perdurou até o final do século XIX. Áreas como mecânica celeste e mecânica dos sólidos eram então estudadas por matemáticos, mas agora são consideradas pertencentes à física.[20] O tema da combinatória foi estudado durante grande parte da história registrada, mas não se tornou um ramo separado da matemática até o século XVII.[21]
No final do século XIX, a crise fundamental da matemática e a resultante sistematização do método axiomático levaram a uma explosão de novas áreas da matemática nunca antes vista.[22][9] A edição de 2020 da Classificação de Disciplinas de Matemática, por exemplo, contém nada menos que 63 áreas matemáticas consideradas de primeiro nível.[23] Algumas delas correspondem à divisão mais antiga, como é o caso da teoria dos números e da geometria. Várias outras têm "geometria" em seus nomes ou são comumente consideradas parte da geometria. Álgebra e cálculo não aparecem como áreas de primeiro nível, mas são campos divididos em várias áreas. Outras áreas de primeiro nível surgiram durante o século XX ou não eram consideradas anteriormente como parte da matemática, como a lógica e os fundamentos matemáticos.[24]
Teoria dos Números

A teoria dos números teve início com as primeiras manipulações dos números naturais e posteriormente expandiu-se para números inteiros e números racionais . Ela já foi chamada de aritmética, mas atualmente este termo é usado principalmente para se referir aos cálculos numéricos.[25] A teoria dos números remonta à antiga Babilônia e provavelmente à China Antiga. Dois proeminentes teóricos deste campo de estudo matemático foram os gregos Euclides e Diofanto de Alexandria.[26] O estudo moderno da teoria dos números na sua forma abstrata é amplamente atribuído a Pierre de Fermat e Leonhard Euler, mas este campo se concretizou totalmente com as contribuições do francês Adrien-Marie Legendre e do alemão Carl Friedrich Gauss.[27]
Muitos problemas numéricos têm soluções que requerem métodos sofisticados. Um exemplo proeminente é o Último Teorema de Fermat, conjectura descrita no ano de 1637 por Pierre de Fermat, mas que foi provada apenas em 1994 por Andrew Wiles, que usou ferramentas incluindo teoria de esquemas de geometria algébrica, teoria de categorias e álgebra homológica.[28] Outro exemplo é a Conjectura de Goldbach, que afirma que todo número inteiro par maior que 2 é a soma de dois números primos. Declarada em 1742 por Christian Goldbach, permanece sem comprovação, apesar de esforços consideráveis.[29]
A teoria dos números abrange inúmeras subáreas, como teoria analítica dos números, teoria algébrica dos números, geometria dos números (orientada a métodos), equações diofantinas e teoria da transcendência (orientada a problemas).[24]
Geometria
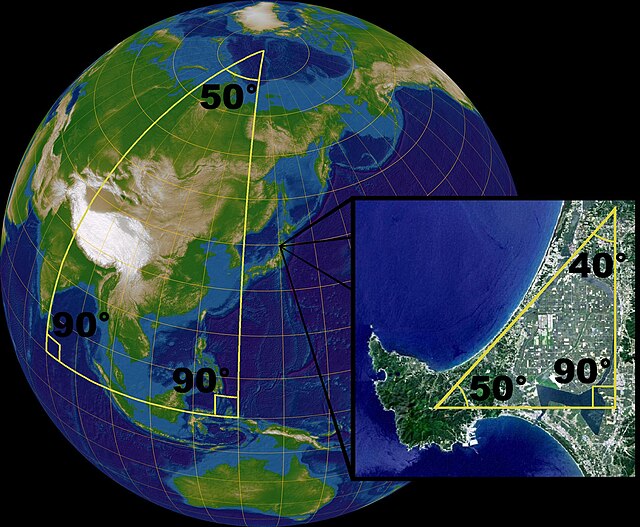
A geometria é um dos ramos mais antigos da matemática e começou com receitas empíricas sobre formas, como linhas, ângulos e círculos, que foram desenvolvidas principalmente para a topografia e a arquitetura, mas desde então floresceram em muitos outros subcampos.[30]
Uma inovação fundamental foi a introdução, pelos antigos gregos, do conceito de provas, que exige que cada afirmação seja provada. Por exemplo, não é suficiente verificar por medição que, digamos, dois comprimentos são iguais; sua igualdade deve ser provada através do raciocínio a partir de resultados previamente aceitos (teoremas) e de algumas afirmações básicas que não estão sujeitas a prova porque são evidentes (postulados) ou que fazem parte da definição do objeto de estudo (axiomas). Este princípio, fundamental para toda a matemática, foi elaborado pela primeira vez para a geometria e foi sistematizado por Euclides por volta do ano 300 a.C. em sua obra Os Elementos.[31][32]
A geometria euclidiana é o estudo das formas e seus arranjos construídos a partir de retas, planos e círculos no plano e no espaço euclidiano tridimensional.[c][30] Foi desenvolvida sem mudança de métodos ou escopo até o século XVII, quando René Descartes introduziu o que hoje é chamado de coordenadas cartesianas, o que constituiu uma grande mudança de paradigma: em vez de definir números reais como comprimentos de segmentos de reta (ver reta numérica), permitiu a representação de pontos usando suas coordenadas, que são números. A álgebra (e mais tarde o cálculo) pode, portanto, ser usada para resolver problemas geométricos. A geometria foi dividida em dois novos subcampos: geometria sintética, que utiliza métodos puramente geométricos, e geometria analítica, que utiliza coordenadas sistemicamente.[33] A geometria analítica permite o estudo de curvas não relacionadas a círculos e linhas. Tais curvas podem ser definidas como o gráfico de funções, cujo estudo levou à geometria diferencial. Elas também podem ser definidas como equações implícitas, muitas vezes equações polinomiais (que geraram a geometria algébrica). A geometria analítica também permite considerar espaços euclidianos superiores a três dimensões.[30]
A geometria analítica permite o estudo das curvas não relacionadas a círculos e linhas que podem ser definidas como o gráfico de funções, cujo estudo levou ao surgimento da área da geometria diferencial. Tais curvas também podem ser definidas como equações implícitas, muitas vezes equações polinomiais (que geraram a geometria algébrica). A geometria analítica também permite considerar espaços euclidianos superiores a três dimensões.[30]
No século XIX, os matemáticos descobriram geometrias não euclidianas, ou seja, que não seguem o postulado das paralelas. Ao questionar a verdade deste postulado, esta descoberta foi interpretada como uma adesão ao Paradoxo de Russell ao revelar a crise fundamental da matemática. Este aspecto da crise foi resolvido por meio da sistematização do método axiomático e pela noção de que a verdade dos axiomas escolhidos, na verdade, não é um problema matemático.[34][9] Por sua vez, o método axiomático permite o estudo de diversas geometrias obtidas quer pela alteração dos axiomas, quer pela consideração de propriedades que não mudam sob transformações específicas do espaço.[35]
As subáreas atuais da geometria incluem:[24]
- Geometria projetiva, introduzida no século XVI por Girard Desargues, estende a geometria euclidiana adicionando pontos impróprios nos quais linhas paralelas se cruzam. Isto simplifica muitos aspectos da geometria clássica, unificando os tratamentos para linhas paralelas e que se cruzam.
- Geometria afim, o estudo das propriedades relativas ao paralelismo e independentes do conceito de comprimento.
- Geometria diferencial, o estudo de curvas, superfícies e suas generalizações, que são definidas por meio de funções diferenciáveis.
- Teoria múltipla, o estudo de formas que não estão necessariamente incorporadas em um espaço maior.
- Geometria riemanniana, o estudo das propriedades de distância em espaços curvos.
- Geometria algébrica, o estudo de curvas, superfícies e suas generalizações, que são definidas por meio de polinômios.
- Topologia, estudo das propriedades que se mantêm sob deformações contínuas.
- Topologia algébrica, o uso em topologia de métodos algébricos, principalmente álgebra homológica.
- Geometria discreta, o estudo de configurações finitas em geometria.
- Geometria convexa, estudo de conjuntos convexos.
- Geometria complexa, a geometria obtida pela substituição de números reais por números complexos.
Álgebra


A álgebra é a arte de manipular equações e fórmulas. Diofanto (século III) e Alcuarismi (século IX) foram os dois principais precursores deste campo de estudo matemático.[37][38] O grego Diofanto resolveu algumas equações envolvendo números naturais desconhecidos ao deduzir novas relações até obter a solução. O persa Alcuarismi, por sua vez, introduziu métodos sistemáticos para transformar equações, como mover um termo de um lado de uma equação para o outro lado. O termo "álgebra" é derivado da palavra árabe al-jabr que significa 'a reunião de partes quebradas' que ele usou para nomear um desses métodos no título de seu tratado principal.[39]
A álgebra tornou-se uma área independente apenas com François Viète (1540-1603), que introduziu o uso de variáveis para representar números desconhecidos ou não especificados.[40]
Até o século XIX, a álgebra consistia principalmente no estudo de equações lineares (atualmente álgebra linear) e de equações polinomiais em uma única incógnita, que eram chamadas de equações algébricas (termo ainda em uso, embora possa ser ambíguo). Durante o século XIX, os matemáticos começaram a usar variáveis para representar outras coisas além dos números (como matrizes, inteiros modulares e transformações geométricas), nas quais generalizações de operações aritméticas são frequentemente válidas.[41] O conceito de estrutura algébrica aborda isto, consistindo em um conjunto cujos elementos não são especificados, em operações que atuam sobre os elementos do conjunto e em regras que essas operações devem seguir. O escopo da álgebra cresceu assim para incluir o estudo de estruturas algébricas. Este objeto da álgebra foi denominado álgebra moderna ou álgebra abstrata, conforme estabelecido pela influência e trabalhos da matemática alemã Emmy Noether.[42]
Alguns tipos de estruturas algébricas têm propriedades úteis e muitas vezes fundamentais em muitas áreas da matemática. Seu estudo tornou-se parte autônoma da álgebra e inclui vários campos de estudos:[24]
- Teoria dos grupos;
- Teoria de campo;
- Espaços vetoriais, cujo estudo é essencialmente igual ao da álgebra linear;
- Teoria dos anéis;
- Álgebra comutativa, que é o estudo dos anéis comutativos, inclui o estudo dos polinômios e é uma parte fundamental da geometria algébrica;
- Álgebra homológica;
- Álgebra de Lie e teoria dos Grupos de Lie;
- Álgebra booliana, que é amplamente utilizada para o estudo da estrutura lógica de computadores.
O estudo de tipos de estruturas algébricas como objetos matemáticos é o propósito da álgebra universal e da teoria das categorias.[43] Esta última se aplica a todas as estruturas matemáticas (não apenas às algébricas). Na sua origem foi introduzida juntamente com a álgebra homológica por permitir o estudo algébrico de objetos não algébricos como espaços topológicos; esta área específica de aplicação é chamada de topologia algébrica.[44]
Cálculo e análise

O cálculo, anteriormente chamado de cálculo infinitesimal, foi introduzido de forma independente e simultânea por dois matemáticos do século XVII, Newton e Leibniz.[45] É fundamentalmente o estudo da relação de variáveis que dependem umas das outras. O cálculo foi expandido no século XVIII por Euler com a introdução do conceito de função e muitos outros resultados.[46]
Atualmente, “cálculo” refere-se principalmente à parte elementar desta teoria, e “análise” é comumente usada para partes avançadas. A análise é subdividida em análise real, onde as variáveis representam números reais, e análise complexa, onde as variáveis representam números complexos. Ela inclui muitas subáreas compartilhadas por outras áreas da matemática como:[24]
- Cálculo multivariável;
- Análise funcional, onde variáveis representam funções variáveis;
- Integração, teoria da medida e teoria do potencial, todas fortemente relacionadas com a teoria das probabilidades num continuum;
- Equações diferenciais ordinárias;
- Equações diferenciais parciais;
- Análise numérica, dedicada principalmente ao cálculo em computadores de soluções de equações diferenciais ordinárias e parciais que surgem em muitas aplicações.
Matemática discreta

A matemática discreta, em termos gerais, é o estudo de objetos matemáticos individuais e contáveis.[47] Como os objetos de estudo aqui são discretos, os métodos de cálculo e análise matemática não se aplicam diretamente.[d] Algoritmos — especialmente sua implementação e complexidade computacional — desempenham um papel importante na matemática discreta.[48]
O teorema das quatro cores e a conjectura de Kepler foram dois grandes problemas da matemática discreta resolvidos na segunda metade do século XX.[49] O problema P versus NP, que permanece não solucionado até os dias atuais, também é importante para a matemática discreta, uma vez que sua solução impactaria potencialmente um grande número de problemas computacionalmente difíceis.[50]
A matemática discreta inclui:[24]
- Combinatória, a arte de enumerar objetos matemáticos que satisfazem algumas restrições. Originalmente, estes objetos eram elementos ou subconjuntos de um determinado conjunto; isto foi estendido a vários objetos, o que estabelece uma forte ligação entre a combinatória e outras partes da matemática discreta. Por exemplo, a geometria discreta inclui a contagem de configurações de formas geométricas;
- Teoria dos grafos e hipergrafos;
- Teoria da codificação, incluindo códigos de correção de erros e uma parte da criptografia;
- Teoria matróide;
- Geometria discreta;
- Distribuições de probabilidade discretas;
- Teoria dos jogos (embora os jogos contínuos também sejam estudados, os jogos mais comuns, como xadrez e pôquer, são discretos);
- Otimização discreta, incluindo otimização combinatória, programação inteira, programação com restrições.
Lógica matemática e teoria dos conjuntos
A disciplinas de lógica matemática e teoria dos conjuntos pertencem à matemática desde o final do século XIX.[51][52] Antes deste período, os conjuntos não eram considerados objetos matemáticos, e a lógica, embora usada em provas matemáticas, pertencia à filosofia e não era estudada especificamente pelos matemáticos.[53]
Antes do estudo de Cantor sobre conjuntos infinitos, os matemáticos relutavam em considerar coleções realmente infinitas e consideravam o infinito o resultado de uma enumeração infinita. O trabalho de Cantor ofendeu muitos matemáticos não apenas por considerar conjuntos realmente infinitos,[54] mas por mostrar que isto implica em diferentes tamanhos de infinito, de acordo com o argumento de diagonalização de Cantor.[55] Esta se tornou a crise fundamental da matemática.[56] Posteriormente, este problema foi resolvido na matemática convencional, ao sistematizar o método axiomático dentro de uma teoria de conjuntos formalizada. A grosso modo, cada objeto matemático é definido pelo conjunto de todos os objetos semelhantes e pelas propriedades que esses objetos devem ter.[22] Por exemplo, na aritmética de Peano, os números naturais são definidos por "zero é um número", "cada número tem um sucessor único", "cada número exceto zero tem um antecessor único" e algumas regras de raciocínio.[57] Esta abstração matemática da realidade está incorporada na filosofia moderna do formalismo, fundada por David Hilbert por volta de 1910.[58]
A "natureza" dos objetos definidos desta forma é um problema filosófico que os matemáticos deixam para os filósofos, mesmo que muitos matemáticos tenham opiniões— por vezes chamada de "intuições" — sobre isto e as usem para orientar o seu estudo e provas. A abordagem permite considerar "lógicas" (isto é, conjuntos de regras de dedução permitidas), teoremas, provas, etc, como objetos matemáticos e, assim, provar teoremas sobre eles. Por exemplo, os teoremas da incompletude de Gödel afirmam, a grosso modo, que, em todo sistema formal consistente que contém os números naturais, existem teoremas que são verdadeiros (que são demonstráveis num sistema mais forte), mas não demonstráveis dentro do sistema.[59] Esta abordagem aos fundamentos da matemática foi desafiada durante a primeira metade do século XX por matemáticos liderados por Brouwer, que promoveram a lógica intuicionista, que carece explicitamente da lei do terceiro excluído.[60][61] Estes problemas e debates acadêmicos levaram a uma ampla expansão da abrangência da lógica matemática, com o surgimento de subáreas como teoria dos modelos (modelagem de algumas teorias lógicas dentro de outras teorias), teoria da prova, teoria dos tipos, teoria da computabilidade e teoria da complexidade computacional.[24] Embora estes aspectos da lógica matemática tenham sido introduzidos antes do surgimento dos computadores, a sua utilização no design de compiladores, certificação de programas e outros aspectos da ciência da computação, contribuíram para a expansão destas teorias lógicas.[62]
Estatísticas e outras ciências de decisão

O campo de estudo da estatística é uma aplicação matemática empregada para a coleta e o processamento de amostras de dados, por meio do uso de procedimentos baseados em métodos matemáticos, especialmente a teoria das probabilidades. Os estatísticos geram dados com experimentos ou amostragem aleatória,[64] cujo desenho determina os métodos analíticos que serão utilizados. A análise dos dados de estudos observacionais é feita pela utilização de modelos estatísticos e da teoria da inferência, por meio de modelos de seleção e estimativa. Os modelos e as previsões consequentes devem então ser testados em relação a novos dados.[e]
A teoria estatística estuda problemas de decisão como a minimização do risco de uma ação estatística ao usar um procedimento, por exemplo, estimativa de parâmetros, teste de hipóteses e seleção de algoritimos. Nestas áreas tradicionais da estatística matemática, um problema de decisão estatística é formulado minimizando uma função de perda sob restrições específicas. Por exemplo, conceber uma pesquisa estatística frequentemente envolve minimizar o custo de estimar a média da população com alguma confiança.[65] Devido ao uso da otimização, a teoria estatística se sobrepõe a outras ciências da decisão, como a pesquisa operacional, a teoria do controle e a economia matemática.[66]
Matemática computacional
A matemática computacional é o estudo de problemas matemáticos que normalmente são grandes demais para a capacidade numérica dos seres humanos.[67][68] A análise numérica estuda métodos para problemas de análise utilizando a análise funcional e a teoria de aproximação; a análise numérica inclui o estudo de aproximação e discretização com foco especial em erros de arredondamento.[69]
Remove ads
História
Resumir
Perspectiva
Antiguidade


A história da matemática é uma série cada vez maior de abstrações. Evolutivamente falando, a primeira abstração a ser descoberta, compartilhada por muitos animais,[70] foi provavelmente a dos números: a constatação de que, por exemplo, uma coleção de duas maçãs e uma coleção de duas laranjas (digamos) têm algo em comum, nomeadamente que existem duas delas. Além de reconhecerem como contar objetos físicos, os povos pré-históricos também podem ter sabido contar quantidades abstratas, como o tempo — dias, estações ou anos.[71][72]
As primeiras evidências de matemática mais complexa só começam a aparecer por volta de 3.000 a.C., quando os povos babilônios e egípcios iniciam o uso de aritmética, álgebra e geometria para estimar seus impostos e fazer outros cálculos financeiros voltados para construção e astronomia.[73] Os textos matemáticos mais antigos da Mesopotâmia e do Egito datam de 2000 a.C. a 1800 a.C.. Muitos textos antigos mencionam triplos pitagóricos e assim, por inferência, o teorema de Pitágoras parece ser o conceito matemático mais antigo e difundido depois da aritmética e geometria básicas. É na matemática babilônica que a aritmética elementar (adição, subtração, multiplicação e divisão) aparece pela primeira vez no registro arqueológico. Os babilônios também possuíam um sistema de valor posicional e usavam um sistema de numeração sexagesimal que ainda é usado atualmente para medir ângulos e o tempo.[74]
No século VI a.C., a matemática grega começou a emergir como uma disciplina distinta e alguns gregos antigos, como os pitagóricos, pareciam tê-la considerado um assunto por direito próprio.[75] Por volta do ano 300 a.C., Euclides organizou o conhecimento matemático por meio de postulados e primeiros princípios, que evoluíram para o método axiomático usado atualmente na matemática, que consiste em definição, axioma, teorema e prova matemáticas.[76] Sua obra, Os Elementos, é amplamente considerada o livro didático de maior sucesso e influência de todos os tempos.[77] O maior matemático da antiguidade é frequentemente considerado Arquimedes (c. 287) de Siracusa.[78] Ele desenvolveu fórmulas para calcular a área superficial e o volume de sólidos de revolução e usou o método da exaustão para calcular a área sob o arco de uma parábola com a soma de uma série infinita, de uma maneira não muito diferente do cálculo moderno.[79] Outras conquistas notáveis da matemática grega são seções cônicas (Apolônio de Perga, século III a.C.),[80] trigonometria (Hiparco de Nicéia, século II a.C.)[81] e os primórdios da álgebra (Diofanto, século III d.C.).[82]

O sistema de numeração hindu-arábico e as regras para o uso de suas operações, em uso atualmente em todo o planeta, evoluíram no decorrer do primeiro milênio na Índia e foram transmitidos ao mundo ocidental através da matemática islâmica.[83] Outros desenvolvimentos notáveis da matemática indiana incluem a moderna definição e aproximação de seno e cosseno, além de uma forma inicial de séries infinitas.[84][85]
Medieval e posterior

Durante a Idade de Ouro Islâmica, especialmente durante os séculos IX e X, a matemática islâmica desenvolveu várias inovações importantes baseadas na matemática grega. A conquista mais notável da matemática islâmica foi o desenvolvimento da álgebra. Outras conquistas do período islâmico incluem avanços na trigonometria esférica e a adição do ponto decimal ao sistema de numeração arábico.[86] Muitos matemáticos notáveis deste período eram persas, como Alcuarismi, Omar Caiam e Xarafadim de Tus.[87] Os textos matemáticos gregos e árabes foram, por sua vez, traduzidos para o latim durante a Idade Média e reintroduzidos na Europa.[88]
No início da Idade Moderna, a matemática começou a desenvolver-se em ritmo acelerado na Europa Ocidental, com inovações revolucionárias, como a introdução de variáveis e da notação simbólica pelo francês François Viète (1540–1603), a introdução de logaritmos pelo escocês John Napier em 1614, que simplificou bastante os cálculos numéricos, especialmente para astronomia e navegação marítima, a introdução de coordenadas pelo francês René Descartes (1596-1650) para reduzir a geometria à álgebra, além do desenvolvimento do cálculo pelo inglês Isaac Newton (1642-1726/27) e pelo alemão Gottfried Leibniz (1646–1716). O suíço Leonhard Euler (1707-1783), o mais notável matemático do século XVIII, unificou todas estas inovações com uma terminologia padronizada e completou-as com a descoberta e a prova de vários teoremas.[89]

Talvez o principal matemático do século XIX tenha sido o alemão Carl Gauss, conhecido por ter feito inúmeras contribuições nos mais variados campos, como álgebra, análise, geometria diferencial, teoria das matrizes, teoria dos números e estatística.[90] Já no início do século XX, o austríaco Kurt Gödel transformou a matemática ao publicar os seus teoremas da incompletude, que mostram em parte que qualquer sistema axiomático consistente — se for suficientemente poderoso para descrever a aritmética — conterá proposições verdadeiras que não podem ser provadas.[59]
Desde então, a matemática foi bastante ampliada e tem havido uma interação frutífera com as ciências, com benefícios para ambas. Descobertas matemáticas continuam a ser feitas até os dias atuais. Por exemplo, de acordo com a edição de janeiro de 2006 do Bulletin of the American Mathematical Society: "O número de artigos e livros incluídos no banco de dados da Mathematical Reviews desde 1940 (o primeiro ano de operação da MR) é agora superior a 1,9 milhão e mais de 75 mil itens são adicionados ao banco de dados anualmente. A esmagadora maioria dos trabalhos neste oceano contém novos teoremas matemáticos e suas provas."[91]
Remove ads
Notação simbólica e terminologia
Resumir
Perspectiva

A notação matemática é amplamente utilizada na ciência e na engenharia para representar conceitos e propriedades complexas de forma concisa, inequívoca e precisa. Esta notação consiste em símbolos usados para representar operações, números não especificados, relações e quaisquer outros objetos matemáticos, e depois montá-los em expressões e fórmulas.[92] Mais precisamente, os números e outros objetos matemáticos são representados por símbolos chamados variáveis, que geralmente são letras latinas ou gregas. Operação e relações são geralmente representadas por símbolos ou glifos específicos,[93] como + (mais), × (multiplicação), (integral), = (igual) e < (menor que).[94] Todos esses símbolos são geralmente agrupados de acordo com regras específicas.[95]
A matemática desenvolveu uma terminologia rica que cobre uma ampla variedade de campos que estudam as propriedades de vários objetos e suas interações, sendo que fornecem uma base padrão para a comunicação. Um axioma ou postulado, por exemplo, é uma afirmação matemática considerada verdadeira sem necessidade de prova. Se uma afirmação matemática ainda não foi provada (ou refutada), ela é chamada de conjectura. Através de uma série de argumentos rigorosos empregando raciocínio dedutivo, uma afirmação que é comprovadamente verdadeira torna-se um teorema. Um teorema especializado usado principalmente para provar outro teorema é chamado de lema. Um exemplo comprovado que faz parte de uma conclusão mais geral é denominado corolário.[96]
Vários termos técnicos usados em matemática são neologismos, como polinômio e homeomorfismo.[97] Outros termos técnicos são palavras da linguagem comum usadas com um significado preciso que pode diferir ligeiramente do seu significado comum. Por exemplo, em matemática, "ou" significa "um, o outro ou ambos", enquanto, na linguagem comum, é ambíguo ou significa "um ou outro, mas não ambos" (em matemática, o último é chamado de "ou exclusivo"). Muitos termos matemáticos são palavras comuns usadas com um significado completamente diferente.[98]
Remove ads
Relação com as ciências
Resumir
Perspectiva
A matemática é usada na maioria das ciências para modelar fenômenos, o que permite que previsões sejam feitas a partir de leis experimentais.[99] A independência da matemática de qualquer experimentação implica que a precisão de tais previsões depende apenas da adequação do modelo.[100] No caso de previsões imprecisas, ao invés delas serem causadas por conceitos matemáticos inválidos, na verdade implicam na necessidade de alteração do modelo utilizado.[101] Por exemplo, a precessão do periélio do planeta Mercúrio só pôde ser explicada após o desenvolvimento da relatividade geral do alemão Albert Einstein, que substituiu a lei da gravitação universal do inglês Isaac Newton como um modelo matemático melhor.[102]
Atualmente, ainda há um debate filosófico sobre se a matemática pode ser classificada como uma ciência. No entanto, na prática, os matemáticos são normalmente considerados cientistas e a matemática tem muito em comum com as ciências físicas, já que é falsificável como elas, o que significa em que, se um resultado ou uma teoria estiverem errados, isto pode ser provado por meio da apresentação de um contraexemplo. Da mesma forma que na ciência, as teorias e os resultados matemáticos (teoremas) são frequentemente obtidos a partir da experimentação,[103] que pode consistir na computação de exemplos selecionados ou no estudo de figuras ou de outras representações de objetos matemáticos (muitas vezes representações mentais sem suporte físico). Por exemplo, quando questionado sobre como conseguiu seus teoremas, Gauss certa vez respondeu "durch planmässiges Tattonieren" ("através de experimentação sistemática").[104] Contudo, alguns autores enfatizam que a matemática difere da noção moderna de ciência por não se basear em evidências empíricas.[105][106][107][108]
Matemática pura e aplicada
Até ao século XIX, o desenvolvimento da matemática no mundo ocidental era motivado principalmente pelas necessidades trazidas pela tecnologia e ciência, sendo que não havia uma distinção clara entre matemática pura e aplicada.[109] Por exemplo, os números naturais e a aritmética foram introduzidos pela necessidade de contagem, enquanto a geometria foi motivada pela topografia, arquitetura e astronomia. Mais tarde, Isaac Newton introduziu o conceito do cálculo infinitesimal para explicar o movimento dos planetas com sua lei da gravitação universal. Além disso, a maioria dos matemáticos eram cientistas e muitos cientistas também eram matemáticos.[110] Contudo, uma exceção notável ocorreu com a tradição da matemática pura na Grécia Antiga.[111] O problema da fatoração de inteiros, por exemplo, que remonta a Euclides em 300 a.C., não tinha aplicação prática antes de seu uso no criptossistema RSA, que atualmente é amplamente utilizado para a segurança de redes de computadores.[112] No século XIX, matemáticos como os alemães Karl Weierstrass e Richard Dedekind concentraram cada vez mais as suas pesquisas em problemas internos, ou seja, na chamada matemática pura.[109][113] Isto levou à divisão da matemática em matemáticas pura e aplicada, sendo a última geralmente considerada de menor valor entre os puristas matemáticos. No entanto, a linha que diferencia as duas é tênue.[114]
As consequências da Segunda Guerra Mundial levou a um aumento no desenvolvimento da matemática aplicada nos Estados Unidos e em outros lugares.[115][116] Muitas das teorias desenvolvidas para aplicações foram consideradas interessantes do ponto de vista da matemática pura e muitos resultados da matemática pura demonstraram ter aplicações fora da matemática; por sua vez, o estudo destas aplicações poderá fornecer novos desenvolvimentos sobre a “teoria pura”.[117][118] Um exemplo do primeiro caso é a teoria das distribuições, introduzida por Laurent Schwartz para validar cálculos feitos em mecânica quântica, que se tornou imediatamente uma importante ferramenta de análise matemática (pura).[119] Um exemplo do segundo caso é a decidibilidade da teoria de primeira ordem dos números reais, um problema de matemática pura que foi provado verdadeiro por Alfred Tarski, com um algoritmo impossível de implementar devido a uma complexidade computacional bastante elevada.[120] Para obter um algoritmo que possa ser implementado e possa resolver sistemas de equações e desigualdades polinomiais, o matemática estadunidense George Collins introduziu a decomposição algébrica cilíndrica que se tornou uma ferramenta fundamental na geometria algébrica real.[121] Nos dias atuais, a distinção entre matemática pura e aplicada é mais uma questão de objetivo de pesquisa do que uma divisão da matemática em áreas amplas.[122][123] A Classificação de Disciplinas de Matemática, por exemplo, tem uma seção para "matemática geral aplicada", mas não menciona "matemática pura".[24]
Eficácia irracional
A eficácia irracional da matemática é um fenômeno que foi nomeado e explicitado pela primeira vez pelo físico Eugene Wigner[6] e descreve o fato de que muitas teorias matemáticas (mesmo as mais “puras”) têm aplicações fora do seu objeto inicial. Estas aplicações podem estar completamente fora da sua área inicial e podem dizer respeito a fenômenos físicos que eram completamente desconhecidos quando a teoria matemática foi introduzida.[124] Um exemplo notável é a fatoração primária de números naturais que foi descoberta mais de 2 mil anos antes de seu uso comum para comunicações seguras na Internet através do sistema criptográfico RSA.[125] Um segundo exemplo histórico é a teoria das elipses. Elas foram estudadas pelos antigos matemáticos gregos como seções cônicas (isto é, interseções de cones com planos). Quase 2 mil anos depois, Johannes Kepler descobriu que as trajetórias dos planetas são elipses.[126]
Durante o século XIX, o desenvolvimento interno da geometria (ou matemática pura) levou à definição e ao estudo de geometrias não euclidianas, espaços de dimensão superior a três e variedades. Neste período, estes conceitos pareciam totalmente desligados da realidade física. No início do século XX, no entanto, o alemão Albert Einstein desenvolveu a teoria da relatividade que utiliza fundamentalmente estes conceitos, principalmente o espaço-tempo da relatividade restrita é um espaço não euclidiano de dimensão quatro, enquanto o espaço-tempo da relatividade geral é uma variedade (curva) de dimensão quatro.[127][128]
Um aspecto marcante da interação entre matemática e física é quando a matemática impulsiona a pesquisa em física, o que é exemplificado pelas descobertas do pósitron e do bárion . Em ambos os casos, as equações das teorias apresentavam soluções inexplicáveis, o que levou à conjectura da existência de uma partícula desconhecida. Em ambos os casos, estas partículas foram descobertas alguns anos depois através de experiências específicas.[129][130][131]
Ciências específicas
Física

A matemática e a física influenciaram-se mutuamente ao longo da história moderna. A física moderna utliza amplamente a matemática[132] e é também a motivação por trás de grandes desenvolvimentos na matemática.[133]
Informática
A ascensão da tecnologia no século XX abriu caminho para uma nova ciência: a computação.[f] Este campo está intimamente relacionado à matemática de várias maneiras. A ciência da computação teórica, por exemplo, é essencialmente de natureza matemática. Em contrapartida, a informática também se tornou essencial para a obtenção de novos resultados. Este é um grupo de técnicas conhecidas como matemática experimental.[134] O exemplo mais conhecido é o teorema das quatro cores, comprovado em 1976 com a ajuda de um computador. Isto revolucionou a matemática tradicional, onde a regra até então era que o matemático verificasse cada parte da prova. Em 1998, a conjectura de Kepler sobre empacotamento de esferas também parecia ter sido parcialmente comprovada por um computador. Desde então, uma equipe internacional trabalhou na redação de uma prova formal, que foi concluída (e verificada) em 2015.[135] Um grande problema em aberto na ciência da computação teórica é P versus NP, um dos sete Problemas do Prêmio Millennium.[136]
Biologia

A biologia utiliza extensivamente a probabilidade, como por exemplo na ecologia ou na neurobiologia.[137] A maior parte do debate sobre probabilidade em biologia, entretanto, centra-se no conceito de aptidão evolutiva.[137]
A ecologia usa amplamente a modelagem para simular a dinâmica populacional,[137][138] estudar ecossistemas como o modelo predador-presa, medir a difusão da poluição,[139] ou para avaliar as mudanças climáticas.[140] A dinâmica de uma população pode ser modelada por equações diferenciais acopladas, como as equações de Lotka-Volterra.[141] No entanto, existe o problema da validação do modelo. Isto é particularmente grave quando os resultados da modelização influenciam as decisões políticas; a existência de modelos contraditórios poderia permitir às nações escolher o modelo mais favorável.[142]
Ciências sociais
As áreas da matemática utilizadas nas ciências sociais incluem probabilidade/estatística e equações diferenciais, que são usadas em linguística, economia, sociologia[143] e psicologia.[144]

O postulado fundamental da economia matemática é o do ator individual racional – Homo economicus (lit. "homem econômico").[145] Neste modelo, o indivíduo busca maximizar seu interesse próprio[145] e sempre faz escolhas ótimas usando informações perfeitas.[146] Contudo, muitas pessoas rejeitaram ou criticaram o conceito.[146] Economistas observam que pessoas reais têm informações limitadas, fazem escolhas erradas e se preocupam com a justiça, o altruísmo e não apenas com o ganho pessoal.[146]
No início do século XX, houve um desenvolvimento no sentido de expressar movimentos históricos através de fórmulas. Por exemplo, em 1922, Nikolai Kondratiev discerniu o ciclo Kondratiev de aproximadamente 50 anos, que explica fases de crescimento ou de crise econômica.[147] No final do século XIX, Nicolas-Remi Brück e Charles Henri Lagrange estenderam suas análises à geopolítica.[148] Desde a década de 1990, o antropólogo evolucionário russo-americano,Peter Turchin trabalha no desenvolvimento da cliodinâmica.[149]
Mesmo assim, a matematização das ciências sociais não é isenta de perigos. No polêmico livro Imposturas Intelectuais (1997), Sokal e Bricmont denunciaram o uso infundado ou abusivo de terminologia científica, especialmente da matemática ou da física, nas ciências sociais.[150]
Remove ads
Relação com astrologia e esoterismo
Alguns matemáticos renomados também foram considerados astrólogos renomados; por exemplo, Ptolomeu, astrônomos árabes, Regiomontano, Cardano, Kepler, ou John Dee. Na Idade Média, a astrologia era considerada uma ciência que incluía a matemática. Em sua enciclopédia, o físico suíço Theodor Zwinger escreveu que a astrologia era uma ciência matemática que estudava o "movimento ativo dos corpos à medida que agem sobre outros corpos" e reservou à matemática a necessidade de “calcular com probabilidade as influências [das estrelas]” para prever suas “conjunções e oposições”.[151] Atualmente, no entanto, a astrologia não é mais considerada uma ciência, mas sim uma pseudociência.[152]
Remove ads
Filosofia
Resumir
Perspectiva
Realidade
A conexão entre a matemática e a realidade material levou a debates filosóficos pelo menos desde a época de Pitágoras. O antigo filósofo Platão argumentou que as abstrações que refletem a realidade material têm elas próprias uma realidade que existe fora do espaço e do tempo. Como resultado, a visão filosófica de que os objetos matemáticos existem de alguma forma por si mesmos na abstração é muitas vezes referida como platonismo. Independentemente das suas possíveis opiniões filosóficas, os matemáticos modernos podem ser geralmente considerados platônicos, uma vez que pensam e falam dos seus objetos de estudo como objetos reais.[153]
O matemático suíço Armand Borel resumiu esta visão da realidade matemática da seguinte forma, e forneceu citações de G. H. Hardy, Charles Hermite, Henri Poincaré e Albert Einstein que apoiam seus pontos de vista.[129]
Algo se torna objetivo (em oposição a "subjetivo") assim que estamos convencidos de que existe nas mentes dos outros da mesma forma que existe nas nossas e que podemos pensar sobre isso e discuti-lo juntos.[154] Como a linguagem da matemática é tão precisa, ela é ideal para definir conceitos para os quais existe tal consenso. Na minha opinião, isso é suficiente para nos fornecer um sentimento de uma existência objetiva, de uma realidade matemática...
Entretanto, o platonismo e as visões concorrentes sobre a abstração não explicam necessariamente a eficácia irracional da matemática.[155]
Definições propostas
Não existe um consenso geral sobre uma definição de matemática ou o seu estatuto epistemológico — isto é, o seu lugar entre outras atividades humanas.[156][157] Muitos matemáticos profissionais não têm interesse em uma definição ou consideram a matemática como algo indefinível.[156] Sequer há consenso sobre se a matemática pode ser considerada uma arte ou uma ciência.[157] Alguns estudiosos apenas dizem que a “matemática é o que os matemáticos fazem”.[156] Isto faz sentido, pois existe um forte consenso entre eles sobre o que a matemática é e não é. A maioria das definições propostas tenta definir a matemática pelo seu objeto de estudo.[158]
Aristóteles definiu a matemática como “a ciência da quantidade” e esta definição prevaleceu até o século XVIII. No entanto, ele também observou que o foco apenas na quantidade pode não distinguir a matemática de ciências como a física; em sua opinião, a abstração e o estudo da quantidade como uma propriedade "separável no pensamento" das instâncias reais diferenciam a matemática.[159] No século XIX, quando os matemáticos começaram a abordar temas que não têm uma relação clara com a realidade física, como os conjuntos infinitos, foram dadas uma variedade de novas definições.[160]
Outra abordagem para definir matemática é fazer uso de seus métodos. Assim, uma área de estudo pode ser qualificada como matemática desde que possa provar teoremas, ou seja, afirmações cuja validade depende de uma prova, isto é, de uma dedução puramente lógica.[161] Outros, no entanto, assumem a perspectiva de que a matemática é uma investigação da teoria axiomática dos conjuntos, já que este estudo é atualmente uma disciplina fundamental para grande parte da matemática moderna.[162]
Rigor
O raciocínio matemático requer rigor. Isso significa que as definições devem ser absolutamente inequívocas e as provas devem ser redutíveis a uma sucessão de aplicações de regras de inferência,[g] sem qualquer uso de evidência empírica e intuição.[h][163] O raciocínio rigoroso não é específico da matemática, mas o padrão de rigor é muito mais alto do que em outros campos de estudo. Apesar da concisão da matemática, provas rigorosas podem exigir centenas de páginas para serem expressas. O surgimento de provas assistidas por computador permitiu que os comprimentos das provas se expandissem ainda mais,[i][164] como o teorema de Feit-Thompson de 255 páginas.[j] O resultado desta tendência é uma filosofia da prova quase empirista, mas que não pode ser considerada infalível.[9]
O conceito de rigor na matemática remonta à Grécia Antiga, onde a sociedade incentivava o raciocínio lógico e dedutivo. No entanto, o rigor tenderia a desencorajar a exploração de novas abordagens, tais como números irracionais e conceitos de infinito. O método de demonstração de provas rigorosas foi aprimorado ao longo do século XVI através do uso de notação simbólica. Durante o século XVIII, a transição social permitiu que os matemáticos passassem a ganhar seu sustento através do ensino, o que levou a uma reflexão mais cuidadosa sobre os conceitos subjacentes à matemática e produziu abordagens mais rigorosas durante a transição de métodos geométricos para provas algébricas e depois aritméticas.[9]
No final do século XIX, parecia que as definições dos conceitos básicos da matemática não eram suficientemente precisas para evitar paradoxos (geometria não euclidiana e função de Weierstrass) e contradições (paradoxo de Russell), o que foi resolvido pela inclusão de axiomas nas regras de inferência apodítica das teorias matemáticas; a reintrodução do método axiomático iniciado pelos antigos gregos antigos.[9] "Rigor" não é mais um conceito relevante em matemática, pois uma prova ou é correta ou é errônea, sendo que uma "prova rigorosa" é simplesmente um pleonasmo. Onde um conceito especial de rigor é aceito é nos aspectos socializados de uma prova, onde pode ser comprovadamente refutado por outros matemáticos. Depois de uma prova ter sido aceita por muitos anos ou mesmo décadas, ela pode então ser considerada confiável.[165] No entanto, o conceito de “rigor” ainda pode continuar sendo útil para ensinar aos iniciantes o que é uma prova matemática.[166]
Remove ads
Treinamento e prática
Resumir
Perspectiva
Educação
A matemática tem uma capacidade evidente de cruzar fronteiras culturais e períodos de tempo. Como atividade humana, a prática da matemática tem um aspecto social, que inclui educação, profissão, reconhecimento, popularização e assim por diante. Na educação, a matemática é uma parte central do currículo e constitui um elemento importante das disciplinas acadêmicas do grupo STEM. Carreiras proeminentes para matemáticos profissionais incluem professor de matemática, estatístico, atuário, analista financeiro, economista, contador, consultor de informática, entre outras.[167]
Evidências arqueológicas mostram que o ensino da matemática ocorreu já no segundo milênio a.C., na antiga Babilônia.[168] Evidências comparáveis foram descobertas nos escribas no Antigo Oriente Próximo e depois no mundo greco-romano, começando por volta do ano 300 a.C..[169] O livro didático de matemática mais antigo conhecido é o Papiro de Rhind, datado de c. 1650 a.C. no Egito Antigo.[170] Devido à escassez de livros, os ensinamentos matemáticos na Índia Antiga foram repassados através da tradição oral memorizada desde o período védico (c. 1500-500 a.C.).[171] Na China Imperial, durante a dinastia Tang (618-907 d.C.), um currículo de matemática foi adotado para concursos públicos para ingressar na burocracia estatal.[172]
Após a Idade das Trevas, a educação matemática na Europa era ministrada por escolas religiosas como parte do Quadrívio. A instrução formal em pedagogia começou nas escolas jesuítas ao longo dos séculos XVI e XVII. A maior parte do currículo matemático, no entanto, permaneceu em um nível básico e prático até o século XIX, quando começou a florescer na França e na Alemanha. O periódico mais antigo abordando o ensino de matemática foi L'Enseignement Mathématique, que começou a ser publicado no ano de 1899.[173] Os avanços do mundo ocidental na ciência e na tecnologia levaram ao estabelecimento de sistemas educativos centralizados em muitos Estados-nação, sendo a matemática um componente central — inicialmente por conta das suas aplicações militares.[174] Embora o conteúdo dos cursos varie, atualmente quase todos os países ensinam matemática aos seus alunos.[175]
Durante a escola, as capacidades matemáticas e as expectativas positivas têm uma forte associação com o interesse profissional na área. Fatores extrínsecos, como apoio de professores, pais e grupos de pares, podem influenciar o nível de interesse pela matemática.[176] Alguns alunos que estudam matemática podem desenvolver apreensão ou medo em relação ao seu desempenho na matéria, o que é conhecido como ansiedade matemática ou fobia matemática e é considerado o mais proeminente dos distúrbios que afetam o desempenho acadêmico. Isto pode se desenvolver devido a vários fatores, como atitudes dos pais e professores, estereótipos sociais e características pessoais. A ajuda para neutralizar este problema pode advir de mudanças nas abordagens instrucionais, de interações com pais e professores e de tratamentos personalizados para cada estudante.[177]
Psicologia (estética, criatividade e intuição)
A validade de um teorema matemático depende apenas do rigor da sua prova, que teoricamente poderia ser feita automaticamente por um programa de computador. Isto não significa que não há lugar para criatividade num trabalho matemático. Pelo contrário, muitos resultados matemáticos importantes (teoremas) são soluções de problemas que outros matemáticos não conseguiram resolver e a invenção de uma forma de resolução pode ser uma forma fundamental do processo de resolução.[178][179] Um exemplo extremo é o teorema de Roger Apéry, cujo autor forneceu apenas as ideias para uma prova e a prova formal foi dada apenas alguns meses depois por três outros matemáticos.[180]
A criatividade e o rigor não são os únicos aspectos psicológicos da atividade dos matemáticos. Alguns deles podem ver a sua atividade como um jogo. Este aspecto da atividade matemática é enfatizado na matemática recreativa.[181] Os matemáticos podem encontrar um valor estético para o seu campo de estudo. Assim como a beleza, a matemática é difícil de definir, está comumente relacionada à elegância, que envolve qualidades como simplicidade, simetria, completude e generalidade. G. H. Hardy, em sua obra Apologia do Matemático, expressou a crença de que as considerações estéticas são, em si, suficientes para justificar o estudo da matemática pura. Ele também identificou outros critérios, como significância, imprevisibilidade e inevitabilidade, que contribuem para a estética matemática.[182] Paul Erdős expressou este sentimento de forma mais irônica ao falar de "O Livro", uma suposta coleção divina das mais belas provas. A obra literária Provas conforme O Livro de 1998, inspirado no livro de Erdős, é uma coleção de argumentos matemáticos particularmente sucintos e reveladores. Alguns exemplos de resultados particularmente elegantes incluídos são a prova de Euclides de que existem infinitos números primos e a transformada rápida de Fourier para análise harmônica.[183]
Alguns acham que considerar a matemática uma ciência é subestimar a sua arte e história nas sete artes liberais tradicionais.[184] Uma forma desta diferença de ponto de vista se manifestar é no debate filosófico sobre se os resultados matemáticos são criados (como na arte) ou descobertos (como na ciência).[129]
Remove ads
Impacto cultural
Resumir
Perspectiva
Expressão artística

Notas musicais que soam bem juntas para um ouvido ocidental são sons cujas frequências fundamentais de vibração estão em proporções simples. Por exemplo, uma oitava duplica a frequência e uma quinta justa multiplica-a por .[185][186]
Os humanos, assim como alguns outros animais, consideram os padrões simétricos mais bonitos.[187] Matematicamente, as simetrias de um objeto formam um grupo conhecido como grupo de simetria.[188]
Por exemplo, o grupo subjacente à simetria do espelho é o grupo cíclico de dois elementos, . Um teste de Rorschach é uma figura invariante por esta simetria,[189] assim como os corpos de borboletas e animais em geral (pelo menos na superfície).[190] As ondas na superfície do mar possuem simetria de translação: mover o ponto de vista pela distância entre as cristas das ondas não altera a visão do mar. Fractais possuem autossimilaridade.[191][192]
Popularização
A matemática popular é o ato de apresentar a matemática sem termos técnicos.[193] Apresentar matemática pode ser difícil, uma vez que o público em geral sofre de ansiedade matemática e os objetos matemáticos são altamente abstratos.[194] No entanto, a escrita matemática popular pode superar isto usando aplicativos ou referências culturais.[195]
Prêmios
Resumir
Perspectiva

O prêmio de maior prestígio em matemática é a Medalha Fields,[196][197] criada em 1936 e concedida a cada quatro anos (exceto por volta da Segunda Guerra Mundial) a até quatro indivíduos.[198][199] É considerado o equivalente matemático do Prêmio Nobel.[199]
Outros prêmios de matemática de prestígio incluem:[200]
- O Prêmio Abel, instituído em 2002[201] e concedido pela primeira vez em 2003;[202]
- A Medalha Chern pelo conjunto da obra, introduzida em 2009[203] e concedida pela primeira vez em 2010;[204]
- O Prêmio AMS Leroy P. Steele, concedido desde 1970;[205]
- O Prêmio Wolf de Matemática, também pelo conjunto da obra,[206] instituído em 1978.[207]
Uma famosa lista de 23 problemas em aberto, chamada "problemas de Hilbert", foi compilada em 1900 pelo matemático alemão David Hilbert.[208] Esta lista alcançou grande celebridade entre os matemáticos[209] e, desde 2022, pelo menos treze dos problemas (dependendo de como alguns são interpretados) foram resolvidos.[208]
Uma nova lista de sete problemas importantes, intitulada "Problemas do Prêmio Millennium", foi publicada no ano 2000. Apenas uma delas, a Hipótese de Riemann, duplica um dos problemas de Hilbert. Uma solução para qualquer um desres problemas acarreta uma recompensa de 1 milhão de dólares.[210] Até hoje, apenas um destes problemas, a Conjectura de Poincaré, foi resolvido.[211]
Remove ads
Ver também
Notas
- Aqui, álgebra é tomada em seu sentido moderno, que é, grosso modo, a arte de manipular fórmulas.
- Isso inclui seções cônicass, que são interseções de cilindros circulares e planos.
- No entanto, alguns métodos avançados de análise são por vezes utilizados; por exemplo, métodos de análise complexa aplicados à função geradora.
- Como outras ciências matemáticas, como física e ciência da computação, a estatística é uma disciplina autônoma e não um ramo da matemática aplicada. Assim como os físicos pesquisadores e os cientistas da computação, os estatísticos pesquisadores são cientistas matemáticos. Muitos estatísticos são formados em matemática e alguns estatísticos também são matemáticos.
- Ada Lovelace é conhecida por ter escrito, na década de 1840, o primeiro programa de computador em colaboração com Charles Babbage
- Isto não significa tornar explícitas todas as regras de inferência utilizadas. Pelo contrário, isto geralmente é impossível, sem computadores e assistentes de prova. Mesmo com esta tecnologia moderna, podem ser necessários anos de trabalho humano para redigir uma prova matemática completamente detalhada.
Ligações externas
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads








